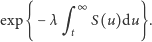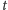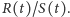Rekordy długowieczności i procesy Poissona II
W pierwszej części artykułu szukaliśmy prawdopodobieństwa tego, że umierający człowiek będzie starszy od wszystkich aktualnie żyjących. Zadanie wykonaliśmy. Obliczyliśmy interesujące nas prawdopodobieństwo. Pozwólmy sobie teraz na kilka komentarzy i dygresji. Przypomnijmy najważniejszy wynik pomocniczy, który udowodniliśmy przed miesiącem.
Stwierdzenie 1. Prawdopodobieństwo tego, że
osobnik umierający w wieku
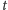 lat jest starszy od wszystkich aktualnie
żyjących, jest równe
lat jest starszy od wszystkich aktualnie
żyjących, jest równe

Warto przyjrzeć się bliżej funkcji
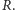 Wyobraźmy sobie, że mamy „bardzo
liczną” próbkę losową osobników o funkcji przeżycia
Wyobraźmy sobie, że mamy „bardzo
liczną” próbkę losową osobników o funkcji przeżycia
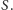 Spodziewamy
się, że spośród wszystkich
Spodziewamy
się, że spośród wszystkich
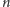 osobników liczba tych, którzy przeżyją
przynajmniej
osobników liczba tych, którzy przeżyją
przynajmniej
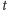 lat, jest bliska
lat, jest bliska
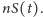 Tak jak w poprzednich
rozważaniach, podzielmy przedział
Tak jak w poprzednich
rozważaniach, podzielmy przedział
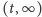 na krótkie odcinki
na krótkie odcinki
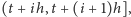 gdzie
gdzie
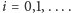 Oczekujemy, że około
Oczekujemy, że około
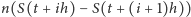 osobników w naszej próbce będzie
miało długość życia w
osobników w naszej próbce będzie
miało długość życia w
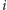 -tym przedziale, czyli w przybliżeniu
-tym przedziale, czyli w przybliżeniu
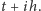 Jeśli teraz obliczymy średnią długość życia ponad
Jeśli teraz obliczymy średnią długość życia ponad
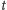 lat, to otrzymamy
lat, to otrzymamy

 wartością
oczekiwaną lub średnią czasu życia ponad
wartością
oczekiwaną lub średnią czasu życia ponad
 lat. Zauważmy, że
mówimy tu o średniej pośród wszystkich osobników. Uznajemy, że ci,
którzy wieku
lat. Zauważmy, że
mówimy tu o średniej pośród wszystkich osobników. Uznajemy, że ci,
którzy wieku
 nie dożyli, mają czas trwania życia ponad
nie dożyli, mają czas trwania życia ponad
 lat
równy 0. Jeśli obliczymy średnią pośród tylko tych osobników, którzy
dożyli wieku
lat
równy 0. Jeśli obliczymy średnią pośród tylko tych osobników, którzy
dożyli wieku
 to otrzymamy
to otrzymamy
 Poniższy wynik ma,
z oczywistych względów, duże znaczenie dla ubezpieczeń życiowych.
Poniższy wynik ma,
z oczywistych względów, duże znaczenie dla ubezpieczeń życiowych.
W szczególności, średnia długość życia jest równa
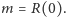
W realnych populacjach średnia długość życia jest skończona. Jednak
z matematycznego punktu widzenia nic nie stoi na przeszkodzie, aby rozważać
takie funkcje przeżycia
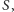 że pole pod wykresem
że pole pod wykresem
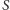 jest
nieskończone, czyli
jest
nieskończone, czyli
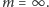 Każda taka nierosnąca funkcja
Każda taka nierosnąca funkcja
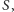 że
że
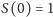 i
i
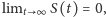 jest poprawną matematycznie funkcją
przeżycia! W świecie, w którym obowiązują reguły T1, T2, N1, N2 i TN
i jednocześnie
jest poprawną matematycznie funkcją
przeżycia! W świecie, w którym obowiązują reguły T1, T2, N1, N2 i TN
i jednocześnie
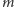 jest nieskończone, pewne zjawiska mogą się wydać
paradoksalne.
jest nieskończone, pewne zjawiska mogą się wydać
paradoksalne.
Wniosek 1. Jeśli średnia długość życia jest nieskończona, to w momencie śmierci każdego osobnika żyje nieskończenie wielu innych osobników od niego starszych.
Nikt nie jest nigdy najstarszy! Nieco dokładniej, teza Wniosku 1 jest zdarzeniem losowym, które zachodzi z prawdopodobieństwem równym 1.
Dowód Wniosku 1. Zdarzenie losowe, o którym mówi Stwierdzenie 1,
zachodzi wtedy i tylko wtedy, gdy w obszarze
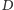 na rysunku 2
nie ma ani jednego końca „odcinka życia” (por. Rys. 1). Jeśli
na rysunku 2
nie ma ani jednego końca „odcinka życia” (por. Rys. 1). Jeśli
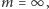 to
to
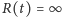 dla każdego
dla każdego
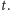 Stosując formalnie
wzór, widzimy, że w obszarze
Stosując formalnie
wzór, widzimy, że w obszarze
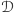 nie ma „punktów śmierci”
z prawdopodobieństwem
nie ma „punktów śmierci”
z prawdopodobieństwem
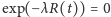 (można to uzasadnić nieco
porządniej, modyfikując tylko nieznacznie podany poprzednio dowód).
Z prawdopodobieństwem 1, w obszarze
(można to uzasadnić nieco
porządniej, modyfikując tylko nieznacznie podany poprzednio dowód).
Z prawdopodobieństwem 1, w obszarze
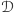 leży zatem przynajmniej
jeden punkt. Nazwijmy teraz
leży zatem przynajmniej
jeden punkt. Nazwijmy teraz
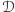 „obszarem zaczepionym w punkcie
„obszarem zaczepionym w punkcie
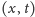 ” i zauważmy, że w nim jest zawarty każdy obszar zaczepiony
w
” i zauważmy, że w nim jest zawarty każdy obszar zaczepiony
w
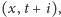 dla
dla
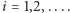
W każdym z tych „mniejszych obszarów” leży przynajmniej jeden punkt,
a zatem w obszarze
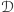 leży nieskończenie wiele punktów, czego
mieliśmy dowieść.
leży nieskończenie wiele punktów, czego
mieliśmy dowieść.
Z drugiej strony, w świecie, w którym obowiązują reguły T1, T2, N1,
N2 i TN i jednocześnie
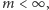 też dzieją się rzeczy osobliwe.
też dzieją się rzeczy osobliwe.
Wniosek 2. Jeśli średnia długość życia jest skończona, to w dowolnym, ustalonym momencie z niezerowym prawdopodobieństwem liczba aktualnie żyjących osobników jest równa zeru.
Co jakiś czas świat całkowicie się wyludnia. Na szczęście, nasze aksjomaty zapewniają, że dzieci będą rodzić się nieprzerwanie, z jednakową intensywnością.
Dla ułatwienia dodajmy, że ten wzór wynika natychmiast z naszych
poprzednich rozważań i zależy tylko od
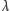 i
i
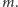
W tytule tego artykułu procesy Poissona występują w liczbie mnogiej.
Założenia N mówią, że proces urodzeń jest jednorodnym procesem
Poissona. Można wywnioskować, powołując się na Założenia T i TN, że
proces zgonów jest też jednorodnym procesem Poissona z tą samą
intensywnością
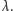 Żeby zobaczyć jeszcze jeden proces Poissona,
zauważmy następujący fakt.
Żeby zobaczyć jeszcze jeden proces Poissona,
zauważmy następujący fakt.
Stwierdzenie 3. Zdarzenie polegające na tym, że w „krótkim” odcinku
czasu
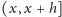 nastąpi śmierć osobnika, który narodził się
w „krótkim” odcinku
czasu
nastąpi śmierć osobnika, który narodził się
w „krótkim” odcinku
czasu
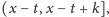 ma prawdopodobieństwo w przybliżeniu
równe
ma prawdopodobieństwo w przybliżeniu
równe
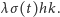 Prawdopodobieństwo śmierci więcej niż jednego
osobnika jest tak małe, że możemy je zaniedbać.
Prawdopodobieństwo śmierci więcej niż jednego
osobnika jest tak małe, że możemy je zaniedbać.
Innymi słowy, możemy rozpatrywane zdarzenie wyrazić tak: w „małym
równoległoboku” na płaszczyźnie znajdzie się jeden „punkt śmierci”. Widać
tu analogię z warunkiem N1. Mały równoległobok można zastąpić,
na przykład, „małym prostokątem”
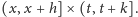 Można
udowodnić własność analogiczną do N2: liczby punktów w rozłącznych
obszarach są statystycznie niezależne. Losowy zbiór „punktów śmierci” jest
procesem Poissona na półpłaszczyźnie
Można
udowodnić własność analogiczną do N2: liczby punktów w rozłącznych
obszarach są statystycznie niezależne. Losowy zbiór „punktów śmierci” jest
procesem Poissona na półpłaszczyźnie
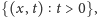 z intensywnością
z intensywnością
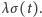 Jest to proces jednorodny względem
Jest to proces jednorodny względem
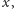 ale niejednorodny
względem
ale niejednorodny
względem
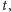 bo jego intensywność zależy od
bo jego intensywność zależy od
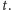 Niestety,
nie możemy tu kontynuować opowieści o procesach Poissona. Czytelnik
może sięgnąć do pięknej książki Kingmana Procesy Poissona, PWN,
Warszawa, 2002.
Niestety,
nie możemy tu kontynuować opowieści o procesach Poissona. Czytelnik
może sięgnąć do pięknej książki Kingmana Procesy Poissona, PWN,
Warszawa, 2002.
* * *
Na zakończenie popatrzmy na badane przez nas zjawisko z perspektywy statystycznej.
W tym celu udamy się na wyprawę do Symulandii. Jest to mały, wyspiarski
kraj, którego mieszkańcy rodzą się i umierają ściśle według reguł
T, N i TN. Funkcja przeżycia jest dokładnie taka, jak na rysunku 3
(znanym już z poprzedniej części artykułu), w szczególności
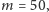 intensywność procesu urodzin jest równa
intensywność procesu urodzin jest równa
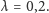
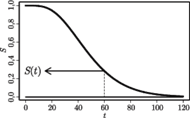
Rys. 3 Wykres funkcji przeżycia.
Co więcej, Główny Symulandzki Urząd Statystyczny dysponuje pełnymi danymi
dotyczącymi osób, które urodziły się lub umarły w przedziale czasowym
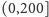 (według lokalnego kalendarza).
(według lokalnego kalendarza).
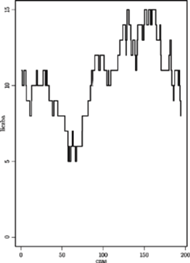
Rys. 4 Liczba ludności Symulandii.
Dane dotyczą 82 osób i składają się z par
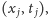 gdzie
gdzie
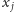 jest
czasem urodzenia,
jest
czasem urodzenia,
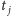 jest długością życia
jest długością życia
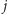 -tej osoby
-tej osoby
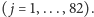 Obliczyliśmy na ich podstawie kilka statystyk, które
teraz przytoczymy. Są to „empiryczne odpowiedniki” wielkości, które
analizowaliśmy.
Obliczyliśmy na ich podstawie kilka statystyk, które
teraz przytoczymy. Są to „empiryczne odpowiedniki” wielkości, które
analizowaliśmy.
- W ciągu 200 lat zaobserwowano 44 urodzenia i 46 zgonów.
– Porównaj z liczbą
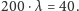
- Średnia długość życia dla 82 osób była równa
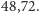
- 21 osób, czyli
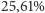 spośród 82 przeżyło ponad 60 lat. – Porównaj
z wartością funkcji przeżycia,
spośród 82 przeżyło ponad 60 lat. – Porównaj
z wartością funkcji przeżycia,
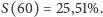
- Średnia długość życia ponad 60 lat, obliczona dla tych
21 osób, była równa
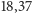 lat. Porównaj z wielkością
lat. Porównaj z wielkością
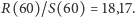
- W ciągu 200 lat ani razu liczba ludności Symulandii nie spadła do 0. – Porównaj z Zagadką 1.
- Średnia liczba ludności Symulandii w przedziale 200 lat była
równa
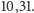 – Porównaj z Zagadką 2 i z rysunkiem 4
(
– Porównaj z Zagadką 2 i z rysunkiem 4
(
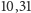 jest to nic innego, jak pole pod wykresem liczby
ludności, podzielone przez 200).
jest to nic innego, jak pole pod wykresem liczby
ludności, podzielone przez 200).
- Na koniec statystyka
dla nas najważniejsza. Spośród 46 zgonów 12 razy zdarzył
się rekord długowieczności w sensie przez nas rozpatrywanym.
– Porównaj ułamek
 z liczbą
z liczbą
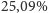 obliczoną zgodnie z uzyskanym przed miesiącem
wzorem
obliczoną zgodnie z uzyskanym przed miesiącem
wzorem