O długowiecznych pchłach i twierdzeniu ergodycznym
czyli co dzieje się z łańcuchami Markowa po długim czasie...
Przypomnijmy jedno z zagadnień, którym zajmowaliśmy się w pierwszej
części artykułu (Delta 9/2013). Pchła poruszała się między ziemią
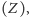 psem
psem
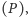 kotem
kotem
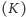 i człowiekiem
i człowiekiem
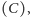 za
każdym razem przeskakując w jedno z pozostałych dopuszczalnych
położeń. Prawdopodobieństwo wyboru każdego docelowego miejsca skoku
było takie samo i równe 1/3. W momencie, gdy pchła wskakiwała na
człowieka – ginęła. Wyliczyliśmy, że średni czas życia pchły wynosi
3.
za
każdym razem przeskakując w jedno z pozostałych dopuszczalnych
położeń. Prawdopodobieństwo wyboru każdego docelowego miejsca skoku
było takie samo i równe 1/3. W momencie, gdy pchła wskakiwała na
człowieka – ginęła. Wyliczyliśmy, że średni czas życia pchły wynosi
3.
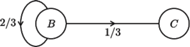
Rys. 1
Zastanówmy się teraz nad nieco innym pytaniem. Jakie jest prawdopodobieństwo
tego, że pchła nadal będzie żyła po wykonaniu
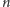 skoków, czyli
– oznaczając przez
skoków, czyli
– oznaczając przez
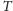 moment śmierci pchły – ile wynosi
moment śmierci pchły – ile wynosi
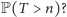 Odpowiedź jest prosta: w każdym swoim skoku pchła albo
wskoczy na człowieka (prawdopodobieństwo 1/3), albo przejdzie do stanu
bezpiecznego (oznaczymy go
Odpowiedź jest prosta: w każdym swoim skoku pchła albo
wskoczy na człowieka (prawdopodobieństwo 1/3), albo przejdzie do stanu
bezpiecznego (oznaczymy go
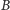 – Rys. 1) – z prawdopodobieństwem
2/3.
– Rys. 1) – z prawdopodobieństwem
2/3.
Moment śmierci to moment pierwszej wizyty w stanie
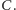 Zatem szukane
prawdopodobieństwo to prawdopodobieństwo przebycia
Zatem szukane
prawdopodobieństwo to prawdopodobieństwo przebycia
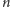 -odcinkowej drogi
-odcinkowej drogi
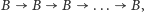 czyli
czyli
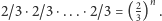 Wielkość
ta maleje wykładniczo i szybko staje się bliska zeru. Na przykład
prawdopodobieństwo tego, że pchła będzie żyła po 10 skokach, to około
Wielkość
ta maleje wykładniczo i szybko staje się bliska zeru. Na przykład
prawdopodobieństwo tego, że pchła będzie żyła po 10 skokach, to około
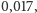 a po 30 skokach:
a po 30 skokach:
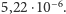
Gdy prawdopodobieństwa przeskoków nie będą zupełnie jednolite, lecz powiedzmy następujące:
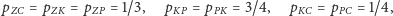 |
albo, na przykład,
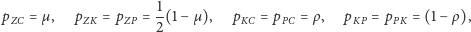 |
to nawet dla niewielkich, byleby wciąż dodatnich wartości
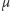 i
i
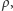 prawdopodobieństwo przeżycia będzie nadal
wykładniczo szybko malało wraz z upływem czasu. W pierwszym przypadku
będziemy mieli ograniczenie
prawdopodobieństwo przeżycia będzie nadal
wykładniczo szybko malało wraz z upływem czasu. W pierwszym przypadku
będziemy mieli ograniczenie
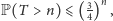 a w drugim –
a w drugim –
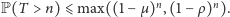
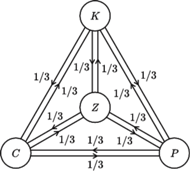
Rys. 2
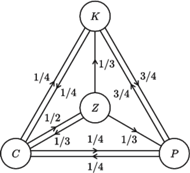
Rys. 3
W sytuacji takiej jak opisana zachowanie po długim czasie nie jest ciekawe: pchła po skończonym czasie zginie (prawie na pewno), a prawdopodobieństwo przeżycia wykładniczo zanika.
No to zrezygnujmy z eksterminacji insektów i przypuśćmy, że pchła może skakać, jak długo chce. Rozpatrzymy dwa przypadki: pierwszy, w którym pchła przeskakuje z człowieka z równym prawdopodobieństwem na ziemię, psa i kota (Rys. 2), oraz bardziej złożony, kiedy człowiek strąca pchłę na podłogę z prawdopodobieństwem 1/2, a z prawdopodobieństwami po 1/4 pchła przeskakuje na jedno ze zwierząt; z kolei z ziemi pchła skacze z takim samym prawdopodobieństwem na człowieka, psa i kota, a ponadto kiedy pchła jest na zwierzęciu, to z prawdopodobieństwem 3/4 przeskakuje na drugie zwierzę, a z prawdopodobieństwem 1/4 – na człowieka (Rys. 3).
W przypadku pierwszym (kiedy graf ma postać taką, jak na rysunku 2) zdrowy
rozsądek podpowiada, że po długim czasie wpływ miejsca startu na to, gdzie
pchła znajdzie się w danej chwili, wygasa, i że dla każdego ze stanów
prawdopodobieństwo zastania tam pchły w danym momencie staje się
w przybliżeniu równe 1/4 (bo przecież pchła gdzieś być musi). Oznaczmy
taki rozkład przez
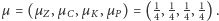 Ma on następującą
ciekawą własność: jeżeli
Ma on następującą
ciekawą własność: jeżeli
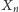 to położenie pchły w chwili
to położenie pchły w chwili
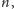 wtedy zakładając, że w chwili
wtedy zakładając, że w chwili
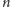 zmienna
zmienna
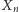 ma rozkład
ma rozkład
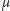 (czyli
(czyli
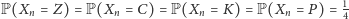 ),
dostaniemy, że
),
dostaniemy, że
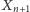 ma też rozkład
ma też rozkład
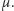
Sprawdźmy:

i tak samo dla pozostałych położeń.
Rozkład o takiej własności nazywamy rozkładem stacjonarnym dla naszego łańcucha Markowa.
Zastanówmy się, czy w drugiej sytuacji, a więc dla łańcucha Markowa o grafie jak z rysunku 3, też istnieje rozkład stacjonarny?
Za pomocą takiego samego rachunku jak wyżej obliczamy, że
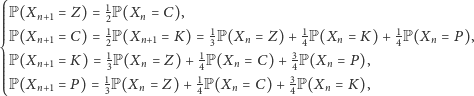 |
czyli składowe rozkładu stacjonarnego muszą spełniać układ równań:
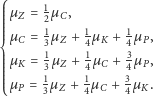 |
Układ ten jest zależny; przekształcając go, otrzymujemy:
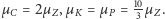 Mamy jednak dodatkową informację –
wiemy przecież, że
Mamy jednak dodatkową informację –
wiemy przecież, że
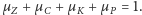 Biorąc to pod uwagę,
dostaniemy:
Biorąc to pod uwagę,
dostaniemy:
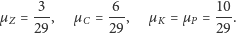 |
A zatem wyznaczyliśmy rozkład stacjonarny. Można też łatwo wywnioskować, że jest on w tym przypadku jedyny.
Czy samo wyznaczenie rozkładu stacjonarnego coś mówi nam o zachowaniu
procesu po długim czasie? Okazuje się, że tak – wynika to z jednej z wersji
tak zwanego twierdzenia ergodycznego dla łańcuchów Markowa.
Aby zwięźle je wysłowić, wprowadźmy kilka oznaczeń. Niech
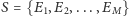 będzie przestrzenią stanów dla łańcucha (w naszym
zadaniu mamy
będzie przestrzenią stanów dla łańcucha (w naszym
zadaniu mamy
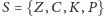 ). Dalej, dla
). Dalej, dla
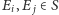 oznaczmy
przez
oznaczmy
przez
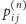 prawdopodobieństwo
prawdopodobieństwo
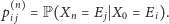 |
Jest to tak zwane prawdopodobieństwo przejścia w
 krokach.
Zakładamy ponadto, że dla dowolnego
krokach.
Zakładamy ponadto, że dla dowolnego
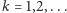 mamy
mamy
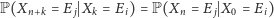 |
(ta własność nazywa się jednorodnością łańcucha w czasie). Dla
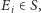 okresem stanu
okresem stanu
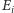 nazywamy liczbę
nazywamy liczbę
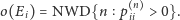 |
Gdy wszystkie stany
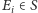 mają okres równy 1, to łańcuch Markowa
nazywa się nieokresowym.
mają okres równy 1, to łańcuch Markowa
nazywa się nieokresowym.
Jesteśmy teraz gotowi, by sformułować potrzebną nam wersję twierdzenia ergodycznego.
Twierdzenie. Niech łańcuch Markowa o przestrzeni stanów
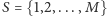 będzie nieokresowy i jednorodny w czasie. Ponadto
załóżmy, że dla dowolnych
będzie nieokresowy i jednorodny w czasie. Ponadto
załóżmy, że dla dowolnych
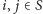 istnieje takie
istnieje takie
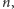 że
że
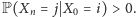 Wtedy istnieje dla niego dokładnie jeden rozkład
stacjonarny
Wtedy istnieje dla niego dokładnie jeden rozkład
stacjonarny
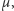 a ponadto dla dowolnych
a ponadto dla dowolnych
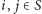 mamy
mamy
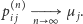 |
Nasz łańcuch spełnia założenia tego twierdzenia: łatwo sprawdzamy,
że jest on nieprzywiedlny, a co do braku okresowości – mamy np.
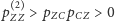 oraz
oraz
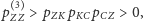 czyli
czyli
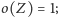 podobnie dla pozostałych stanów.
podobnie dla pozostałych stanów.
Tak naprawdę to nieokresowości pozostałych stanów nie musimy sprawdzać
bezpośrednio: wiadomo bowiem, że jeżeli
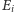 i
i
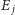 są
takimi stanami, że dla pewnych
są
takimi stanami, że dla pewnych
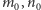 jest
jest
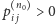 oraz
oraz
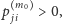 to
to
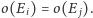
A zatem – mając wyznaczone rozkłady stacjonarne – możemy zastosować
twierdzenie ergodyczne i wywnioskować, że w przypadku łańcucha o grafie
z rysunku 2 prawdopodobieństwa tego, że pchła będzie w konkretnym stanie,
będą faktycznie wszystkie zmierzały do 1/4, natomiast dla łańcucha o grafie 3
asymptotyczne prawdopodobieństwo tego, że pchła będzie na ziemi, to 3/29, na
człowieku
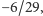 a na kocie lub na psie
a na kocie lub na psie
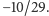
Można zinterpretować to też następująco: wpuściwszy do pokoju mnóstwo
pcheł
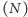 i każąc im się poruszać zgodnie z zasadami naszego
łańcucha, po długim czasie około
i każąc im się poruszać zgodnie z zasadami naszego
łańcucha, po długim czasie około
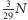 pcheł zastaniemy na ziemi,
pcheł zastaniemy na ziemi,
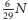 – na człowieku, a najbardziej zapchlone będą zwierzęta: po
– na człowieku, a najbardziej zapchlone będą zwierzęta: po
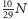 będzie na kocie i na psie.
będzie na kocie i na psie.