W latach sześćdziesiątych ubiegłego wieku John Banzhaf III, matematyk z Massachusetts Institute of Technology, napisał pracę o wiele mówiącym tytule Głosowanie ważone nie działa: matematyczna analiza. Analizował w niej radę hrabstwa Nassau w stanie Nowy Jork. W hrabstwie tym znajdowało się wówczas (i znajduje się po dziś dzień) 5 miast: Hempstead, North Hempstead, Oyster Bay, Glen Cove i Long Beach. Hempstead, które było zdecydowanie największym miastem, podzielone było na dwie strefy: Hempstead I oraz Hempstead II, a podział miejsc w radzie był następujący: Hempstead I (9 miejsc), Hempstead II (9), North Hempstead (7), Oyster Bay (3), Glen Cove (1) i Long Beach (1). Aby ocenić, jaki wpływ na przyjmowane uchwały mają te miasta, Banzhaf analizował, w jakich sytuacjach miasto zmieniając swój głos, zmienia wynik głosowania. Załóżmy na przykład, że tylko miasto North Hempstead popiera uchwałę wnoszącą, aby wybudować na ich terenie park za 10 milionów dolarów. Jeżeli Oyster Bay przychyli się do wniosku, uchwała wciąż nie zostanie podjęta - oba miasta mają razem 10 głosów, a do większości potrzeba ich 16. Z kolei jeśli to Hempstead II (druga strefa miasta Hempstead) zagłosuje "za", uchwała zostanie przyjęta.

Zastanówmy się w ogólności, kto musi zagłosować za uchwałą, aby została ona przyjęta. Jeżeli obie strefy miasta Hempstead zagłosują "za", to będą mieć większość. Tak samo będzie, jeżeli "za" zagłosuje jedna z tych stref oraz miasto North Hempstead. Z kolei jeśli tak nie będzie, tzn. jeżeli "za" będzie tylko jedna ze stref albo tylko miasto North Hempstead, to niezależnie od głosów pozostałych miast większości nie uda się zdobyć. Dochodzimy do zaskakującego wniosku: głosy Oyster Bay, Glen Cove i Long Beach w ogóle się nie liczą! To właśnie zaobserwował Banzhaf i grzmiał w swoim artykule, że nie może być tak, że 16% mieszkańców, bo tylu wtedy mieszkało w tych miastach, nie ma żadnego realnego wpływu na podejmowane decyzje!

Matematycznym modelem do analizy systemów głosowania są gry głosowania ważonego - jedna z najważniejszych klas gier koalicyjnych. Niech 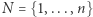będzie naszym zbiorem graczy. Gra głosowania ważonego zapisywana jest jako 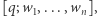gdzie 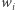to waga gracza 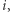która odpowiada jego liczbie głosów, a 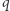oznacza liczbę głosów potrzebnych do przegłosowania uchwały. W radzie hrabstwa Nassau graczami są zatem miasta lub ich strefy i radzie odpowiada gra Grupa graczy, czyli inaczej koalicja, nazywana jest wygrywającą, jeżeli ma w sumie tyle głosów, aby przegłosować ustawę: koalicja 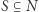jest wygrywająca, jeżeli 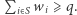W przeciwnym wypadku koalicja jest przegrywająca.

Aby ocenić znaczenie gracza w grze głosowania ważonego, Banzhaf zaproponował, by sprawdzić, jak często jest on kluczowy w koalicji. Gracz 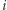jest kluczowy w koalicji 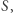jeżeli koalicja jest wygrywająca z nim, a przegrywająca bez niego, tzn. 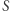jest koalicją wygrywającą, a 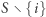- przegrywającą. Ocenę graczy wyznaczamy następująco. Najpierw dla każdego gracza liczymy, w ilu koalicjach jest on kluczowy: 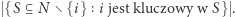Następnie dzielimy tę liczbę przez sumę liczb dla wszystkich graczy, aby ich oceny sumowały się do jedynki. Siła gracza 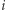w grze 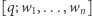opisana jest zatem następującym wzorem:

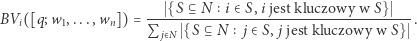Metoda ta powszechnie nazywana jest indeksem siły Banzhafa, chociaż już wcześniej, w 1946 roku, zaproponował ją angielski uczony Lionel Penrose, bardziej znany ze swoich prac dotyczących genetyki niepełnosprawności umysłowej.

Obliczmy, jaki jest rozkład sił w radzie hrabstwa Nassau, przy użyciu nowo poznanej techniki. Gracz 1 jest kluczowy w koalicji, jeżeli zawiera ona jego i dokładnie jednego z graczy 2 i 3. Takich koalicji jest 16: jest 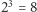koalicji z graczami 1 i 2, ale bez gracza 3 oraz 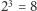koalicji z graczami 1 i 3, ale bez gracza 2. Dla graczy 2 i 3 dostajemy ten sam wynik. Gracze 4, 5 i 6 nie są kluczowi nigdy. We wszystkich koalicjach mamy zatem 48 graczy kluczowych. Rozkład sił, jaki uzyskaliśmy, jest więc następujący:

gdzie kolejno wypisaliśmy indeks siły Banzhafa dla gracza 1, 2 itd.

Szeroko stosowaną alternatywą dla indeksu siły Banzhafa jest indeks siły Shapleya-Shubika, który odpowiada zastosowaniu do gier głosowania ważonego wartości Shapleya, o której już w Delcie pisaliśmy (Rozbijanie sieci terrorystycznych za pomocą teorii gier, Delta 11/2016).

Paradoksy

Analizując indeks siły Banzhafa, możemy przekonać się, jak skomplikowaną i często nieprzewidywalną funkcją jest rozkład sił w parlamencie. Często jeden głos może zmienić sytuację diametralnie.

Załóżmy na przykład, że decyzją administracyjną status miasta otrzymała wieś Atlantic Beach i w radzie przyznano jej dwa miejsca. Dodanie dwóch miejsc zwiększy próg większości do 17 i otrzymamy następującą grę głosowania ważonego: Dodaliśmy nowego gracza, możemy się zatem spodziewać, że istotność istniejących graczy spadnie. Nic bardziej mylnego - okazuje się, że miasta, które mają jednego reprezentanta, czyli gracze 5 i 6, zaczynają się liczyć. Popatrzmy na koalicję 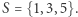Koalicja razem ma 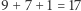głosów, a więc każdy jej głos jest na wagę złota. Gracz 5 jest w niej zatem kluczowy, a jego siła w grze nie jest już zerowa. Łatwo sprawdzić, że jeżeli dokładając gracza z 2 miejscami, nie zwiększylibyśmy progu 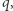czyli uzyskali grę to gracze z jednym głosem także zyskaliby na znaczeniu. Ta obserwacja nazywana jest paradoksem nowego członka.

Załóżmy teraz z kolei, że obie strefy miasta Hempstead zostaną połączone, czyli rozpatrzmy grę Jasne jest, że miasto to staje się wówczas jedynym znaczącym graczem. Może się także zdarzyć, że po złączeniu dwóch graczy ich sumaryczna siła spadnie (tak jest np. w grze w której gracze 1 i 2 mają w sumie siłę 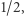a po połączeniu ich siła spada do 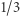). Łączenie partii może więc zarówno pozytywnie, jak i negatywnie wpływać na ich siłę. Ta obserwacja nazywana jest paradoksem wielkości.

Na koniec warto zaznaczyć, że w naszej analizie dokonujemy kilku upraszczających założeń. Po pierwsze zakładamy dyscyplinę partyjną, czyli to, że wszystkie osoby reprezentujące daną partię lub miasto głosują tak samo. Po drugie przyjmujemy, że zawsze wszyscy są obecni, czyli nikt w hrabstwie nie choruje. Po trzecie ustalamy jeden próg potrzebny do przegłosowania dowolnej uchwały, co nie zawsze ma miejsce (np. w polskim sejmie wymagana jest większość konstytucyjna, aby zmienić konstytucję). Po czwarte zakładamy, że wszystkie koalicje są równie prawdopodobne, czyli że nie ma sympatii i antypatii między partiami. Jak odrzucenie tych założeń wpłynęłoby na rozkład sił? To już jest temat na kolejny artykuł.