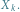Nieprzechodnie kostki i ruletki
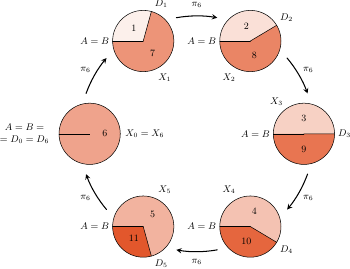
W roku 1970 Martin Gardner opisał w dziale matematycznym czasopisma Scientific American kostki do gry odkryte kilka lat wcześniej przez statystyka Bradleya Efrona...

Kostki te (oznaczmy je 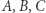 oraz
oraz  ) różnią się od zwykłej kostki tym, że na ich ściankach umieszczone są inne liczby oczek:
) różnią się od zwykłej kostki tym, że na ich ściankach umieszczone są inne liczby oczek:
- kostka
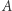 - ma dwie ścianki puste, a na każdej z pozostałych czterech ścianek umieszczone są po 4 oczka;
- ma dwie ścianki puste, a na każdej z pozostałych czterech ścianek umieszczone są po 4 oczka; - kostka
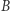 - na każdej ściance znajdują się 3 oczka;
- na każdej ściance znajdują się 3 oczka; - kostka
 - na czterech ściankach znajdują się po 2 oczka, a na dwóch po 6;
- na czterech ściankach znajdują się po 2 oczka, a na dwóch po 6; - kostka
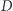 - na trzech ściankach znajduje się po 1 oczku, a na pozostałych po 5.
- na trzech ściankach znajduje się po 1 oczku, a na pozostałych po 5.
Rzucając kostkami 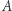 i
i 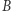 z prawdopodobieństwem
z prawdopodobieństwem 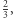 uzyskamy więcej oczek na kostce
uzyskamy więcej oczek na kostce 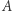 niż na
niż na  Gdy rzucimy
Gdy rzucimy 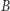 oraz
oraz 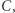 to z prawdopodobieństwem
to z prawdopodobieństwem 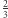 uzyskamy więcej oczek na kostce
uzyskamy więcej oczek na kostce 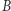 niż na
niż na 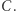 W podobny sposób (za każdym razem z prawdopodobieństwem
W podobny sposób (za każdym razem z prawdopodobieństwem 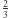 ) kostka
) kostka 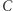 okazuje się lepsza od
okazuje się lepsza od 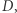 zaś
zaś 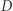 lepsza od
lepsza od 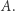 Czyli wśród tych czterech kostek nie ma najlepszej! Ujmując to inaczej: dla każdej kostki z tego zestawu można znaleźć w tym zestawie kostkę lepszą. Przy sortowaniu kostek od najgorszej do najlepszej powstaje cykl (patrz rysunek). Relacja między kostkami, polegająca na byciu lepszą, nie jest przechodnia! Ta nieprzechodniość fascynowała nie tylko matematyków, ale również socjologów i ekonomistów (którzy powiązali ją z teorią wyboru i z modelami użyteczności losowej).
Czyli wśród tych czterech kostek nie ma najlepszej! Ujmując to inaczej: dla każdej kostki z tego zestawu można znaleźć w tym zestawie kostkę lepszą. Przy sortowaniu kostek od najgorszej do najlepszej powstaje cykl (patrz rysunek). Relacja między kostkami, polegająca na byciu lepszą, nie jest przechodnia! Ta nieprzechodniość fascynowała nie tylko matematyków, ale również socjologów i ekonomistów (którzy powiązali ją z teorią wyboru i z modelami użyteczności losowej).
Rozważmy dwuosobową grę: pierwszy gracz wybiera jedną z kostek  drugi wybiera jedną z pozostałych, a następnie obaj rzucają wybranymi kostkami. Wygrywa ten, kto uzyska więcej oczek. Okazuje się, że w tej grze lepiej być drugim graczem, bo wybierając odpowiednio kostkę, wygrywa się z prawdopodobieństwem
drugi wybiera jedną z pozostałych, a następnie obaj rzucają wybranymi kostkami. Wygrywa ten, kto uzyska więcej oczek. Okazuje się, że w tej grze lepiej być drugim graczem, bo wybierając odpowiednio kostkę, wygrywa się z prawdopodobieństwem 
Gra 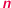 "kostkami"
"kostkami"
Załóżmy, że mamy jakiś inny skończony zbiór przyrządów do losowania liczb (niekoniecznie sześciennych kostek), który dawałby w analogicznej grze dużą szansę wygrania drugiemu graczowi. Jak duża może być ta szansa? Niech 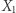 będzie dowolnym przyrządem z tego zbioru, zaś
będzie dowolnym przyrządem z tego zbioru, zaś 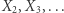 określamy w ten sposób, że
określamy w ten sposób, że  jest tym przyrządem, który wybrałby gracz drugi, gdyby gracz pierwszy wybrał przyrząd
jest tym przyrządem, który wybrałby gracz drugi, gdyby gracz pierwszy wybrał przyrząd 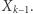 Ponieważ przyrządów jest skończenie wiele, to w którymś momencie muszą zacząć się powtarzać, powstanie cykl. Możemy usunąć ze zbioru wszystkie przyrządy spoza tego cyklu - to może co najwyżej zwiększyć szansę drugiego gracza. Oznaczmy przez
Ponieważ przyrządów jest skończenie wiele, to w którymś momencie muszą zacząć się powtarzać, powstanie cykl. Możemy usunąć ze zbioru wszystkie przyrządy spoza tego cyklu - to może co najwyżej zwiększyć szansę drugiego gracza. Oznaczmy przez 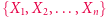 zbiór takich tworzących cykl przyrządów. Niech odpowiedzią gracza drugiego na
zbiór takich tworzących cykl przyrządów. Niech odpowiedzią gracza drugiego na 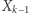 będzie
będzie  (dla
(dla 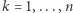 ). Przyjmijmy
). Przyjmijmy 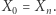 Prawdopodobieństwo tego, że przy optymalnej grze obu graczy drugi wygra, wynosi
Prawdopodobieństwo tego, że przy optymalnej grze obu graczy drugi wygra, wynosi 
Wykażemy, że dla  przyrządów, tworzących cykl, prawdopodobieństwo to może przyjąć wartość co najwyżej
przyrządów, tworzących cykl, prawdopodobieństwo to może przyjąć wartość co najwyżej

Dla zbioru 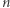 przyrządów prawdopodobieństwo to jest co najwyżej takie, jak dla pewnego cyklu zawartego w tym zbiorze, a więc nie przekracza
przyrządów prawdopodobieństwo to jest co najwyżej takie, jak dla pewnego cyklu zawartego w tym zbiorze, a więc nie przekracza  Z drugiej strony, gdy wszystkie elementy zbioru należą do cyklu długości
Z drugiej strony, gdy wszystkie elementy zbioru należą do cyklu długości  to może ono być równe
to może ono być równe 
Trójkąty 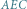 i
i 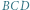 są podobne, a stąd wynika, że
są podobne, a stąd wynika, że

(ostatnia równość wynika z równoramienności  ), czyli
), czyli 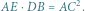
Geometryczne narzędzia
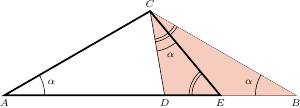
Będziemy potrzebować pewnych geometrycznych obserwacji. Rozważmy taki trójkąt równoramienny 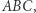 że
że 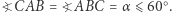 Wybierzmy takie punkty
Wybierzmy takie punkty  oraz
oraz  na boku
na boku  żeby
żeby 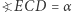 oraz żeby punkt
oraz żeby punkt  leżał bliżej wierzchołka
leżał bliżej wierzchołka  niż punkt
niż punkt  Wówczas
Wówczas 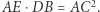
Powtórzmy teraz wielokrotnie wcześniejszą obserwację.
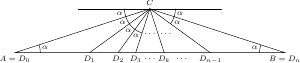
Niech 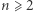 i
i  Wówczas
Wówczas 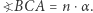 Jeśli punkty
Jeśli punkty 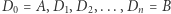 wybierzemy na boku
wybierzemy na boku  w taki sposób, że
w taki sposób, że  dla
dla 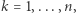 to zachodzi
to zachodzi 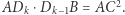
Jesteśmy gotowi, by skonstruować  przyrządów losujących, pozwalających graczowi drugiemu wygrać z prawdopodobieństwem
przyrządów losujących, pozwalających graczowi drugiemu wygrać z prawdopodobieństwem 
Konstrukcja ruletek
Nawińmy odcinek  (czyli najdłuższy bok trójkąta) na koło o środku
(czyli najdłuższy bok trójkąta) na koło o środku  i promieniu
i promieniu  tak, by stał się on obwodem koła. Punkty
tak, by stał się on obwodem koła. Punkty 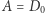 oraz
oraz  ulegną sklejeniu, tworząc jeden punkt, który wraz z punktami
ulegną sklejeniu, tworząc jeden punkt, który wraz z punktami 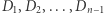 dzieli obwód na
dzieli obwód na 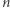 części. Punkty te, oczywiście, nie są równomiernie rozmieszczone na obwodzie, tak samo jak nie były na boku trójkąta. Przyrząd
części. Punkty te, oczywiście, nie są równomiernie rozmieszczone na obwodzie, tak samo jak nie były na boku trójkąta. Przyrząd  (gdzie
(gdzie 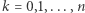 ) to ruletka, którą otrzymujemy, dzieląc koło promieniami
) to ruletka, którą otrzymujemy, dzieląc koło promieniami 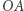 oraz
oraz 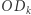 na dwa sektory, w które wpisujemy liczby
na dwa sektory, w które wpisujemy liczby 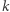 oraz
oraz 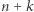 w sposób pokazany na rysunku.
w sposób pokazany na rysunku.
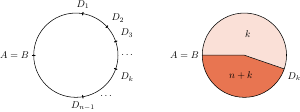
Z lewej szablon do zbudowania  przyrządów, z prawej przyrząd
przyrządów, z prawej przyrząd 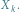
Ruletka działa w naturalny sposób - można, na przykład, zamocować w środku wskazówkę i wprawić ją w ruch, każda jej wynikowa pozycja jest tak samo prawdopodobna, a wynikiem losowania będzie liczba wpisana w pole, na którym się ona zatrzyma. Prawdopodobieństwo uzyskania wyniku 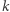 na przyrządzie
na przyrządzie 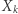 wynosi
wynosi 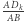 (stosunek długości łuków), zaś prawdopodobieństwo uzyskania wyniku
(stosunek długości łuków), zaś prawdopodobieństwo uzyskania wyniku 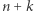 wynosi
wynosi 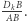 Ruletki
Ruletki 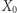 oraz
oraz  są identyczne - zwracają jedynie wynik
są identyczne - zwracają jedynie wynik 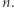 Dla przykładu, dla
Dla przykładu, dla 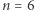 uzyskujemy następujące ruletki:
uzyskujemy następujące ruletki:
Aby obliczyć prawdopodobieństwo tego, z jakim 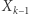 jest mniejsze od
jest mniejsze od  zauważmy, że
zauważmy, że 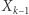 może przyjąć tylko wartości
może przyjąć tylko wartości 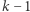 lub
lub 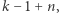 zaś
zaś  tylko wartości
tylko wartości 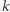 lub
lub 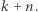 Zatem
Zatem 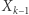 jest mniejsze od
jest mniejsze od  zawsze z wyjątkiem sytuacji, gdy
zawsze z wyjątkiem sytuacji, gdy 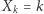 oraz
oraz 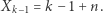 Wynika stąd, że dla
Wynika stąd, że dla 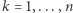


Na kolejnym rysunku zilustrowane są obliczenia dla 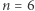 oraz przyrządów
oraz przyrządów 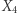 i
i 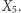 Odcinek
Odcinek 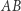 nawijamy na ruletkę
nawijamy na ruletkę 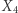 (trójkąt z lewej) i
(trójkąt z lewej) i 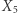 (trójkąt nad kwadratem) w pokazany sposób. Zaznaczamy odpowiednie sektory. Prawdopodobieństwo
(trójkąt nad kwadratem) w pokazany sposób. Zaznaczamy odpowiednie sektory. Prawdopodobieństwo  jest równe stosunkowi pól zacieniowanego prostokąta i kwadratu
jest równe stosunkowi pól zacieniowanego prostokąta i kwadratu 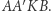 Ponieważ trójkąty
Ponieważ trójkąty 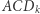 i
i 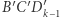 są podobne, to stosunek ten dla dowolnych ruletek
są podobne, to stosunek ten dla dowolnych ruletek  i dowolnego
i dowolnego 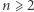 wynosi
wynosi

Wszystkie prostokąty 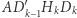 mają takie samo pole równe
mają takie samo pole równe 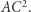 Punkty
Punkty 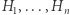 leżą na jednej hiperboli. Wykazaliśmy, jak zbudować
leżą na jednej hiperboli. Wykazaliśmy, jak zbudować 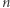 przyrządów realizujących szansę
przyrządów realizujących szansę 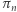 na wygraną drugiego gracza.
na wygraną drugiego gracza.
Dlaczego nie można uzyskać więcej niż 
Załóżmy, że  są takimi niezależnymi zmiennymi losowymi, że
są takimi niezależnymi zmiennymi losowymi, że 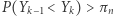 dla wszystkich
dla wszystkich 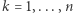 (gdzie
(gdzie 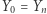 ). Okazuje się (dowód tego faktu nie jest łatwy), że modyfikując odpowiednio nasze zmienne losowe, można założyć, że
). Okazuje się (dowód tego faktu nie jest łatwy), że modyfikując odpowiednio nasze zmienne losowe, można założyć, że 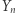 jest stała (tak, jak w przypadku kostki
jest stała (tak, jak w przypadku kostki  w zestawie Efrona oraz ruletki
w zestawie Efrona oraz ruletki 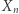 ). Określmy liczby
). Określmy liczby 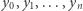 następująco: niech
następująco: niech 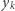 będzie takie, że
będzie takie, że 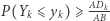 oraz
oraz 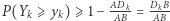 (taka liczba
(taka liczba  to kwantyl rzędu
to kwantyl rzędu 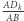 rozkładu zmiennej losowej
rozkładu zmiennej losowej 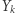 ). Ponieważ
). Ponieważ 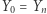 jest stała, więc można liczby
jest stała, więc można liczby 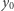 oraz
oraz 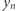 określić tak, by
określić tak, by 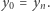 Niech
Niech 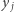 będzie najmniejszą spośród liczb
będzie najmniejszą spośród liczb 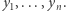 Wówczas
Wówczas 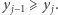 Wynika stąd, że jeśli
Wynika stąd, że jeśli  oraz
oraz 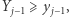 to
to  Zatem
Zatem

Otrzymaliśmy sprzeczność. Oznacza to, że takie zmienne losowe nie istnieją.
Ponieważ ciąg 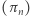 jest rosnący i zbieżny do
jest rosnący i zbieżny do 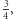 więc prawdopodobieństwo zwycięstwa drugiego gracza jest zawsze mniejsze niż
więc prawdopodobieństwo zwycięstwa drugiego gracza jest zawsze mniejsze niż 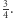
Zauważmy, że 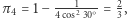 czyli kostki Efrona stanowią optymalny przykład dla
czyli kostki Efrona stanowią optymalny przykład dla 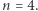 W ciągu
W ciągu 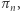 oprócz
oprócz 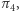 tylko
tylko 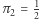 jest liczbą wymierną (wtedy gra nie ma większego sensu, ale takie kostki bez problemu można wskazać). Pozostałe wartości są niewymierne, więc nie można ich zrealizować za pomocą kostek (nawet takich, które mają inną niż
jest liczbą wymierną (wtedy gra nie ma większego sensu, ale takie kostki bez problemu można wskazać). Pozostałe wartości są niewymierne, więc nie można ich zrealizować za pomocą kostek (nawet takich, które mają inną niż 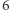 liczbę ścian). Na przykład
liczbę ścian). Na przykład 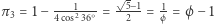 jest stosunkiem długości krótszej do dłuższej części w złotym podziale odcinka (
jest stosunkiem długości krótszej do dłuższej części w złotym podziale odcinka ( 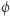 to złota proporcja),
to złota proporcja), 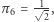
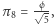 zaś
zaś  Jeszcze inne szczególne wartości
Jeszcze inne szczególne wartości  to
to 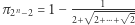 dla
dla 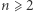 (mamy tu
(mamy tu 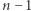 dwójek oraz
dwójek oraz 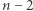 pierwiastki) oraz
pierwiastki) oraz  (tym razem
(tym razem 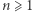 i mamy
i mamy 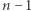 dwójek, jedną trójkę oraz
dwójek, jedną trójkę oraz 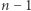 pierwiastków).
pierwiastków).
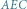 i
i 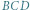 są podobne, a stąd wynika, że
są podobne, a stąd wynika, że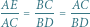
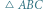 ), czyli
), czyli 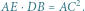
 przyrządów, z prawej przyrząd
przyrządów, z prawej przyrząd