Ostatnio znajomy zapytał mnie, jak wywnioskować, ile jest kart w grze z dwóch następujących własności: 1) każda karta ma 8 symboli, 2) każde dwie karty mają dokładnie jeden wspólny symbol. Spróbujmy na nie odpowiedzieć. Zauważmy najpierw, że jeśli zgubimy którąś z kart, to nadal będziemy mogli grać, czyli nadal spełnione będą dwa powyższe warunki. W związku z tym nie możemy dokładnie określić, ile musi być kart, bo zawsze może być ich mniej. Ciekawe natomiast jest pytanie, ile może być maksymalnie kart w talii.

Na tak sformułowane pytanie możemy odpowiedzieć w sposób wykrętny. Mianowicie możemy wybrać pewien symbol, powiedzmy słonia, i na każdej karcie narysować słonia, a oprócz tego umieścić na różnych kartach różne symbole, które nigdy się nie powtarzają. Nietrudno zauważyć, że możemy stworzyć dowolnie wiele kart, używając tego schematu. W takiej talii kart rzeczywiście każde dwie karty będą miały jeden wspólny symbol, ale zawsze będzie to słoń, gra nie będzie zbyt ciekawa. Dodajmy więc dodatkowe założenie, które spowoduje, że gra będzie nieco bardziej grywalna: 3) nie istnieje symbol, który występuje na wszystkich kartach. Zadajmy więc ponownie pytanie: ile kart może być maksymalnie w takiej talii?

Pokażemy, że taka talia ma co najwyżej 57 kart. Wybierzmy pewną kartę, nazwijmy ją wyróżnioną. Powiedzmy, że narysowane są na niej różne psy, będziemy je nazywać: pies numer 1, pies numer 2, …, pies numer 8. Każda z pozostałych kart zawiera jakiegoś psa, i to dokładnie jednego, bo musi mieć dokładnie jeden wspólny symbol z kartą wyróżnioną. Udowodnimy teraz, że dla każdego 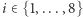poza kartą wyróżnioną jest co najwyżej 7 kart, które zawierają psa numer 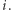Załóżmy bez straty ogólności, że 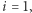dla innych 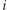dowód jest analogiczny. Ponieważ żaden symbol nie występuje na wszystkich kartach, więc musi istnieć karta, która nie zawiera psa numer 1, nazwijmy ją specjalną. Musi ona jednak zawierać jakiegoś psa, gdyż musi mieć wspólny symbol z kartą wyróżnioną. Załóżmy bez straty ogólności, że karta specjalna zawiera psa numer 2, a oprócz tego 7 kotów: kota numer 1, …, kota numer 7. Zauważmy teraz, że każda karta, która zawiera psa numer 1, musi mieć wspólny symbol z kartą specjalną. Nie zawiera psa numer 2, a więc musi zawierać jakiegoś kota. Z drugiej strony żadne dwie karty, zawierające psa numer 1, nie mogą mieć tego samego kota, bo zawierałyby wtedy dwa wspólne rysunki. Kotów na karcie specjalnej jest 7, a to oznacza, że oprócz karty wyróżnionej jest co najwyżej 7 kart zawierających psa numer 1. W ten sam sposób pokazujemy, że dla dowolnego 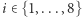oprócz karty wyróżnionej jest co najwyżej 7 kart zawierających psa numer 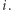A więc w sumie kart w talii jest co najwyżej 7 razy 8 plus 1 wyróżniona, czyli co najwyżej 57.

Na powyższe rozważania można również spojrzeć, używając nieco bardziej zaawansowanych narzędzi geometrii i algebry. Rysunki utożsamiamy wtedy z punktami, a karty będą prostymi, tyle że w przestrzeni rzutowej. Jeśli przestrzeń ta będzie miała wymiar 2 (czyli będzie płaszczyzną) i będzie nad ciałem skończonym wielkości 7, to spełnione będą warunki 1) każda prosta ma 8 punktów oraz 2) każde dwie proste przecinają się w jednym punkcie. Dodatkowo spełniony będzie warunek nawet ogólniejszy niż 3), czyli dla każdego punktu istnieją dwie proste, które przecinają się w tym dokładnie punkcie. Można nietrudno wykazać, że prostych tych będzie 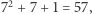co pokazuje, że ograniczenie 57 istotnie da się osiągnąć! Co ciekawe, w grze Dobble jest tylko 55 kart, nie wiadomo zupełnie, dlaczego producenci zdecydowali się usunąć 2 karty.

Podobną konstrukcję kart, zawierających 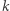symboli każda, można wykonać dla dowolnego 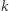takiego, że 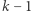jest potęgą liczby pierwszej. Wynika to z faktu, że istnieje ciało skończone o mocy 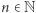wtedy i tylko wtedy, gdy 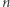jest potęgą liczby pierwszej. Więcej o grze Dobble, skończonych ciałach i płaszczyznach rzutowych można przeczytać w artykule Naprawdę ciekawa gra w Deltcie 4/2014.