Deltoid
Przedłuż ścieżkę
Gra Black rozgrywana jest przez dwóch graczy (I - rozpoczynającego i II) na prostokątnej planszy podzielonej na kwadratowe pola jednostkowe; każdy z wymiarów planszy jest większy od 2...
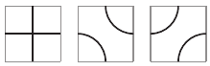
Rys. 1
Gracze na przemian rysują w kwadratach jeden ze wzorów z rysunku 1, przy czym:
- (1)
- gracz I w pierwszym ruchu musi w lewym górnym rogu narysować wzór +,
- (2)
- następnie gracz II gra na sąsiednim polu, przedłużając jedno z ramion +,
- (3)
- każdy gracz musi w swoim ruchu wydłużać czarną ścieżkę wyznaczoną przez pierwsze dwa ruchy (Rys. 2),
- (4)
- przegrywa gracz, który doprowadzi ścieżkę do brzegu planszy.
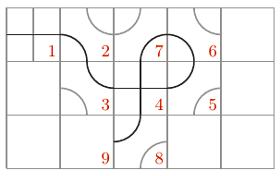
Rys. 2 Przykładowy początek gry, numeracja pól odzwierciedla kolejność ruchów.
W ruchu 7 gracz I doprowadził ścieżkę do pola z numerem 8.
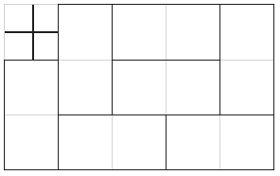
Rys. 3 Podział na kostki domina odpowiadający rozgrywce z Rys. 2
Wiadomo, że w tego rodzaju grach jeden z graczy zawsze ma strategię wygrywającą, czyli może wygrać niezależnie od poczynań przeciwnika. Więcej na ten temat oraz inne gry znaleźć można m.in. w Deltoidzie 10/2009, polecam zwłaszcza zadanie 4.
Warto teraz przerwać lekturę, by pograć w tę grę i poszukać strategii wygrywającej.
Strategię wygrywającą na planszy o nieparzystej liczbie pól ma gracz II. Dzieli całą planszę bez początkowego pola na kostki domina (czyli prostokąty 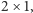 Rys. 3). Łatwo sprawdzić, że taki podział zawsze jest możliwy (jak również inne, dalej opisane). Następnie w każdym swoim ruchu gra w pustej kostce domina tak, aby ścieżka kończyła się w jej środku (a więc nigdy nie doprowadzi jej do krawędzi i nie przegra). Zawsze może to zrobić, gdyż zmusza w ten sposób przeciwnika do dopełnienia tej samej kostki domina, więc sam w kolejnym swym ruchu znów zagra w nowej kostce.
Rys. 3). Łatwo sprawdzić, że taki podział zawsze jest możliwy (jak również inne, dalej opisane). Następnie w każdym swoim ruchu gra w pustej kostce domina tak, aby ścieżka kończyła się w jej środku (a więc nigdy nie doprowadzi jej do krawędzi i nie przegra). Zawsze może to zrobić, gdyż zmusza w ten sposób przeciwnika do dopełnienia tej samej kostki domina, więc sam w kolejnym swym ruchu znów zagra w nowej kostce.
Na planszy o parzystej liczbie pól podobną strategię wygrywającą ma gracz I: po pierwszym ruchu gracza II dzieli całą planszę na kostki domina tak, aby dwa zajęte już pola tworzyły jedną kostkę. Następnie gra jak wyżej.
Zmieńmy teraz regułę (4) na następującą:
- (4')
- przegrywa gracz, który doprowadzi ścieżkę do brzegu planszy, chyba że zrobi to w prawym dolnym rogu (na mecie) - wtedy gracz ten wygrywa.
Poprzednia strategia gracza I dla parzystej liczby pól działa teraz na planszy o nieparzystej liczbie pól z usuniętą metą. W swoim ruchu gracz I zaczyna nowe domino (nie przegrywa) lub trafia na metę (wygrywa).

Rys. 4
Jeśli plansza ma jeden wymiar parzysty, a drugi nieparzysty, gracz II dzieli na domina szachownicę bez pola startowego i mety i też wygrywa jak powyżej.
Pora na przykrą niespodziankę: planszy o obu wymiarach parzystych z usuniętym polem startowym i metą nie da się podzielić na kostki domina. Dlaczego? I jak w takim razie zmodyfikować strategię? Zachęcam do przemyśleń przed dalszą lekturą.
Pomalujmy planszę w szachownicę. Pole startowe i meta są jednego koloru, więc bez nich zostaje inna liczba pól białych niż czarnych (Rys. 4). Tymczasem każda kostka domina ma jedno pole białe i jedno czarne, zatem podział nie jest możliwy.
Nowa strategia dla gracza II: w pierwszym swoim ruchu kieruje on ścieżkę tak, by gracz I musiał zagrać w polu w prawo i w dół od pola startowego (Rys. 5). Gracz I wydłuża ścieżkę, a jednocześnie wybrany przez niego wzór łączy pewne dwa puste pola, oznaczmy każde z nich przez 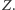
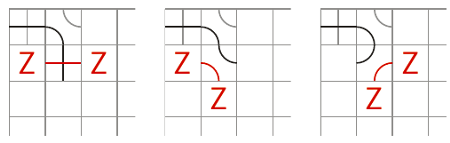
Rys. 5 Lewa górna część planszy, różne warianty po drugim ruchu gracza I.
Teraz gracz II dzieli na kostki domina całą planszę oprócz trzech zajętych już pól, dwóch pól 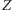 i mety. Taki podział zawsze da się przeprowadzić (nietrudne sprawdzenie tego pozostawiam Czytelnikowi). Ponadto parę pól
i mety. Taki podział zawsze da się przeprowadzić (nietrudne sprawdzenie tego pozostawiam Czytelnikowi). Ponadto parę pól 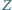 gracz II też uznaje za jedno domino, gdyż pola te są ze sobą połączone. Dalej gra jak zwykle.
gracz II też uznaje za jedno domino, gdyż pola te są ze sobą połączone. Dalej gra jak zwykle.