Co to jest?
Migawki informatyczne
Paradoks Russella
W miejscowości 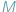 jest fryzjer, nazwijmy go superfryzjerem, który strzyże tych i tylko tych mieszkańców miejscowości, którzy nie strzygą siebie samych. Czy superfryzjer strzyże siebie samego? Chwila namysłu pokazuje, że obie możliwości są wykluczone: nie może on strzyc siebie samego, bo strzyże tylko tych, którzy siebie sami nie strzygą; gdyby zaś sam się nie strzygł, to musiałby się strzyc, bo strzyże wszystkich tych, którzy sami się nie strzygą. A zatem, superfryzjer nie może istnieć! Pokażemy jak z powyższego faktu otrzymać różne twierdzenia matematyczne, odpowiednio definiując mieszkańców miejscowości
jest fryzjer, nazwijmy go superfryzjerem, który strzyże tych i tylko tych mieszkańców miejscowości, którzy nie strzygą siebie samych. Czy superfryzjer strzyże siebie samego? Chwila namysłu pokazuje, że obie możliwości są wykluczone: nie może on strzyc siebie samego, bo strzyże tylko tych, którzy siebie sami nie strzygą; gdyby zaś sam się nie strzygł, to musiałby się strzyc, bo strzyże wszystkich tych, którzy sami się nie strzygą. A zatem, superfryzjer nie może istnieć! Pokażemy jak z powyższego faktu otrzymać różne twierdzenia matematyczne, odpowiednio definiując mieszkańców miejscowości 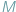 oraz to, kto kogo strzyże.
oraz to, kto kogo strzyże.

Część tych wyników była opisana w artykule Wojciecha Czerwińskiego (Delta 10/2016) poświęconym metodzie przekątniowej, bardzo blisko związanej z paradoksem Russella.
Paradoks Russella
Bertrand Russell używał historii o fryzjerze, by ilustrować następujący problem dotyczący podstaw matematyki, odkryty przez niego w 1901 roku, i mający wielki wpływ na rozwój tej dziedziny. Czym jest zbiór? Chcielibyśmy, by elementami zbiorów mogły być inne zbiory; na przykład, okrąg to zbiór punktów na płaszczyźnie, i można rozważać zbiór wszystkich tych zbiorów, które są na płaszczyźnie okręgami o promieniu 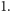 Ogólniej, można by oczekiwać, że dowolne określenie postaci "zbiór wszystkich zbiorów o własności
Ogólniej, można by oczekiwać, że dowolne określenie postaci "zbiór wszystkich zbiorów o własności 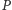 ", gdzie
", gdzie 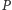 jest precyzyjnie określoną własnością zbiorów, definiuje pewien zbiór. Pokażemy, że tak być nie może. Mieszkańcami
jest precyzyjnie określoną własnością zbiorów, definiuje pewien zbiór. Pokażemy, że tak być nie może. Mieszkańcami 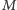 niech będą wszystkie zbiory, i powiemy, że zbiór
niech będą wszystkie zbiory, i powiemy, że zbiór  strzyże zbiór
strzyże zbiór 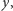 jeżeli
jeżeli 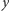 należy do
należy do 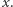 Brak superfryzjera oznacza tyle, że określenie "zbiór wszystkich zbiorów, które nie należą do siebie samych" nie może określać żadnego zbioru.
Brak superfryzjera oznacza tyle, że określenie "zbiór wszystkich zbiorów, które nie należą do siebie samych" nie może określać żadnego zbioru.
Twierdzenie Cantora
Paradoks Russella był zainspirowany dziesięć lat starszą metodą przekątniową Georga Cantora. Cantor zastanawiał się, które zbiory są przeliczalne, tzn. wszystkie ich elementy można wypisać w nieskończonym ciągu 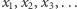 Oczywiście, zbiór liczb naturalnych
Oczywiście, zbiór liczb naturalnych 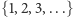 jest przeliczalny, ale też zbiór liczb wymiernych w przedziale
jest przeliczalny, ale też zbiór liczb wymiernych w przedziale 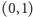 też jest przeliczalny:
też jest przeliczalny:

również zbiór wszystkich liczb wymiernych jest przeliczalny (ćwiczenie dla Czytelnika). Z kolei, zbiór wszystkich liczb rzeczywistych, nawet tych w przedziale 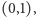 nie jest przeliczalny, co właśnie wykazał Cantor, i my teraz znowu wykażemy. Każda liczba rzeczywista z przedziału
nie jest przeliczalny, co właśnie wykazał Cantor, i my teraz znowu wykażemy. Każda liczba rzeczywista z przedziału 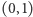 jest określona przez nieskończony ciąg cyfr, np.
jest określona przez nieskończony ciąg cyfr, np. 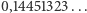 (przy czym nie rozważamy zapisów, które od pewnego momentu mają same cyfry
(przy czym nie rozważamy zapisów, które od pewnego momentu mają same cyfry 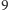 ).
).
Niech 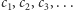 będzie ciągiem liczb rzeczywistych z przedziału
będzie ciągiem liczb rzeczywistych z przedziału 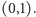 Zdefiniujmy liczbę
Zdefiniujmy liczbę 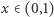 następująco: jej
następująco: jej 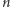 -ta cyfra to
-ta cyfra to 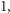 jeśli
jeśli 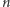 -ta cyfra liczby
-ta cyfra liczby 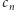 jest równa
jest równa 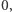 i 0 w przeciwnym przypadku. Wykażemy, że
i 0 w przeciwnym przypadku. Wykażemy, że 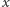 nie pojawia się w ciągu: gdyby
nie pojawia się w ciągu: gdyby 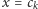 dla pewnego
dla pewnego 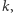 to
to 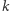 byłoby superfryzjerem w miejscowości
byłoby superfryzjerem w miejscowości 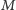 zamieszkałej przez liczby naturalne, w której
zamieszkałej przez liczby naturalne, w której 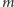 strzyże
strzyże  wtedy, i tylko wtedy, gdy
wtedy, i tylko wtedy, gdy 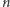 -ta cyfra liczby
-ta cyfra liczby 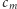 to
to 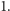 Sprzeczność.
Sprzeczność.

Twierdzenie Turinga
Wybierzmy swój ulubiony język programowania, np. Java, C++, Pascal czy Python (w oryginalnym dowodzie z 1936 r. Alan Turing użył bardzo prostego "języka", zwanego dziś maszyną Turinga). Kod źródłowy programu jest to napis (używający znaków dostępnych na klawiaturze komputera), który jest zgodny ze składnią wybranego języka. Rozważmy programy, których kod źródłowy jest szczególnej postaci 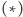 : pierwszą wykonywaną instrukcją jest "wczytaj napis
: pierwszą wykonywaną instrukcją jest "wczytaj napis 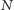 wprowadzony przez użytkownika", potem następuje ciąg instrukcji bez interakcji z użytkownikiem, a ostatnią instrukcją programu jest wypisanie słowa "koniec". Z punktu widzenia nieśmiertelnego użytkownika, który uruchamia taki program i wprowadza napis
wprowadzony przez użytkownika", potem następuje ciąg instrukcji bez interakcji z użytkownikiem, a ostatnią instrukcją programu jest wypisanie słowa "koniec". Z punktu widzenia nieśmiertelnego użytkownika, który uruchamia taki program i wprowadza napis 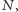 są dwa możliwe scenariusze: albo program po pewnym czasie napisze "koniec" - mówimy wtedy, że program akceptuje napis
są dwa możliwe scenariusze: albo program po pewnym czasie napisze "koniec" - mówimy wtedy, że program akceptuje napis 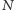 - albo nigdy nic nie napisze, tzn. "zawiesi się". Dla wielu programów, wynik działania na danym napisie
- albo nigdy nic nie napisze, tzn. "zawiesi się". Dla wielu programów, wynik działania na danym napisie 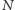 bardzo łatwo przewidzieć. Można by pokusić się o napisanie programu
bardzo łatwo przewidzieć. Można by pokusić się o napisanie programu 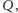 który dostaje na wejściu kod źródłowy dowolnego programu
który dostaje na wejściu kod źródłowy dowolnego programu 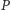 postaci
postaci 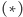 oraz napis
oraz napis 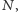 po czym napisze "wiesza się", jeżeli program
po czym napisze "wiesza się", jeżeli program 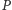 się wiesza dostawszy na wejściu
się wiesza dostawszy na wejściu 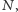 oraz napisze "akceptuje" w przeciwnym przypadku. Twierdzenie Turinga, które teraz udowodnimy, mówi, że taki program
oraz napisze "akceptuje" w przeciwnym przypadku. Twierdzenie Turinga, które teraz udowodnimy, mówi, że taki program 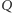 nie może istnieć. Gdyby istniał, to skonstruowalibyśmy program
nie może istnieć. Gdyby istniał, to skonstruowalibyśmy program 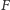 który, dostawszy kod dowolnego programu
który, dostawszy kod dowolnego programu 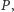 akceptuje go wtedy, i tylko wtedy, gdy program
akceptuje go wtedy, i tylko wtedy, gdy program 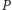 uruchomiony na wejściu
uruchomiony na wejściu 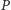 się wiesza, co można stwierdzić, uruchamiając program
się wiesza, co można stwierdzić, uruchamiając program 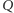 na parze
na parze 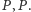 Wtedy
Wtedy 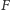 byłby superfryzjerem w miejscowości
byłby superfryzjerem w miejscowości 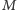 zamieszkałej przez kody źródłowe postaci
zamieszkałej przez kody źródłowe postaci 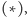 w której
w której 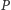 strzyże
strzyże 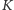 jeśli program
jeśli program 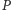 akceptuje
akceptuje 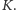 Sprzeczność.
Sprzeczność.
Twierdzenie Gödla o niezupełności
W uproszczeniu, ten wynik z 1931 r. mówi, że istnieje zdanie, którego ani nie da się dowieść, ani dowieść jego zaprzeczenia. Wywnioskujemy to z twierdzenia Turinga. Przez zdanie rozumiemy napis spełniający pewne proste wymagania składniowe. O dowodach zakładamy jedynie tyle, że istnieje program komputerowy, który dostawszy napis 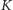 oraz napis
oraz napis 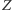 odpowiada w skończonym czasie "poprawny" bądź "niepoprawny", w zależności od tego, czy
odpowiada w skończonym czasie "poprawny" bądź "niepoprawny", w zależności od tego, czy 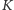 jest poprawnym dowodem zdania
jest poprawnym dowodem zdania 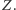 Dodatkowo, każde zdanie, które ma dowód, jest prawdziwe.
Dodatkowo, każde zdanie, które ma dowód, jest prawdziwe.
Przypuśćmy, że dla każdego zdania 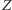 albo istnieje jego dowód, albo dowód zdania "nieprawda, że
albo istnieje jego dowód, albo dowód zdania "nieprawda, że 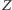 ", oznaczanego
", oznaczanego 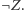 Napiszemy program
Napiszemy program 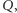 który działa następująco. Rozważmy zdanie
który działa następująco. Rozważmy zdanie 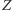 "program
"program 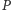 akceptuje napis
akceptuje napis 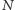 " oraz jego negację
" oraz jego negację 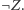 Wczytaj na wejściu kod źródłowy programu
Wczytaj na wejściu kod źródłowy programu 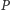 oraz napis
oraz napis 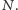 Jeżeli
Jeżeli 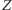 ma dowód, to napisz "akceptuje", a jeżeli
ma dowód, to napisz "akceptuje", a jeżeli 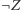 ma dowód, to napisz "wiesza się". Żeby stwierdzić, który przypadek zachodzi, program
ma dowód, to napisz "wiesza się". Żeby stwierdzić, który przypadek zachodzi, program 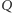 przeszukuje wszystkie (coraz dłuższe) napisy, i dla każdego z nich sprawdza, czy jest dowodem
przeszukuje wszystkie (coraz dłuższe) napisy, i dla każdego z nich sprawdza, czy jest dowodem 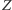 bądź
bądź 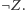 Z naszych założeń wynika, że w skończonym czasie znajdzie dowód albo
Z naszych założeń wynika, że w skończonym czasie znajdzie dowód albo 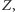 albo
albo 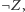 i że opisany program
i że opisany program 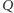 poprawnie przewiduje zachowanie programu
poprawnie przewiduje zachowanie programu 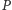 na wejściu
na wejściu 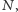 przecząc twierdzeniu Turinga. Musi więc istnieć zdanie, które nie ma dowodu, ani którego zaprzeczenie nie posiada dowodu. Z kolei, z twierdzenia Gödla o pełności z 1929 roku, takie zdanie nie jest ani prawdziwe, ani nieprawdziwe - jest niezależne od przyjętych aksjomatów. Więcej o tym można znaleźć w moim artykule w Delcie 1/2017.
przecząc twierdzeniu Turinga. Musi więc istnieć zdanie, które nie ma dowodu, ani którego zaprzeczenie nie posiada dowodu. Z kolei, z twierdzenia Gödla o pełności z 1929 roku, takie zdanie nie jest ani prawdziwe, ani nieprawdziwe - jest niezależne od przyjętych aksjomatów. Więcej o tym można znaleźć w moim artykule w Delcie 1/2017.
Inne zastosowanie w informatyce
W złożoności obliczeniowej mierzy się, jak "skomplikowana" jest własność liczb naturalnych, tj. ile kroków musi wykonać program, by stwierdzić, czy dana liczba ma tę własność. Przykładowo, własność "liczba parzysta" jest mniej skomplikowana niż własność "liczba pierwsza". Metoda przekątniowa pozwala wszystko znacznie bardziej skomplikować.