Mała Delta
Zadania o przeprawie przez rzekę
Przypomnijmy starą zagadkę o przeprawie przez rzekę...
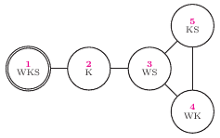
Rys. 1 Oznaczenia: W - wilk, K - koza, S - kapusta; cykl nieparzystej długości: 1, 2, 3, 4, 5, 3, 2, 1 (7 krawędzi).
Zagadka 1. Przewoźnik musi przeprawić się przez rzekę. Wiezie wilka, kozę i kapustę. Jego łódka umożliwia mu wzięcie ze sobą na pokład jednocześnie tylko jednego elementu inwentarza. Dodatkowo jeśli zostawi na brzegu bez opieki wilka z kozą, to wilk pożre kozę. Podobnie kapusta nie przetrwa pozostawiona z kozą. Czy przewoźnik jest w stanie przewieźć cały inwentarz na drugi brzeg?
Ten problem rozwiązujemy za pomocą teorii grafów. Rozważamy możliwe "stany", czyli opisy tego, co się znajduje po której stronie rzeki i analizujemy, z których do których stanów da się przejść (przepłynąć?).
Aby zmniejszyć ilość stanów, umawiamy się, że opisem stanu będzie zbiór tych elementów, które znajdują się tam, gdzie łódka i przewoźnik. Czytelnik Zaniepokojony może protestować. Przecież w takiej definicji niektóre sytuacje "sklejają się", tzn. są opisane przez ten sam stan! Istotnie, jeśli stan nie koduje informacji o tym, po której stronie rzeki znajduje się łódka, to ustawienia symetryczne są dla nas nieodróżnialne. W szczególności sytuacja początkowa i docelowa opisana jest tym samym stanem - zbiorem wszystkich elementów. To jednak nie jest problem. Wystarczy sobie uświadomić, że każdy ruch zmienia pozycję łódki. A więc każda ścieżka, która zaczyna się na jednej stronie rzeki, a kończy na drugiej, musi być nieparzystej długości.
Powyższa obserwacja w zasadzie kończy opis tego rozumowania. Po prostu rysujemy graf możliwych przejść i przekonujemy się, że istnieje w nim cykl nieparzystej długości przechodzący przez stan początkowy (Rys. 1). Zupełnie analogicznie rozwiązujemy kolejne zagadki (Rys. 2, 3).
Zagadka 2. Przez rzekę chce się przeprawić dwoje dorosłych i dwoje dzieci. Mają tratwę, w której mieści się albo jeden dorosły, albo dwójka dzieci (albo oczywiście jedno dziecko). Czy cała grupa może bezpiecznie przedostać się na drugi brzeg?
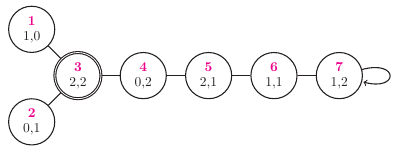
Rys. 2 Napis 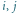 oznacza
oznacza 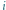 dorosłych oraz j dzieci; cykl nieparzystej długości: 3, 4, 5, 6, 7, 7, 6, 5, 4, 3 (9 krawędzi).
dorosłych oraz j dzieci; cykl nieparzystej długości: 3, 4, 5, 6, 7, 7, 6, 5, 4, 3 (9 krawędzi).
Zagadka 3. Przez rzekę chcą się przeprawić trzy pary rodzeństwa typu brat-siostra. Ich tratwa może pomieścić tylko dwie osoby. Musimy zachować następujące ograniczenie: żaden z braci nie pozwoli, aby jego siostra przebywała w obecności jakiegokolwiek innego mężczyzny, jeśli on sam nie jest przy tym obecny. Czy cała grupa może bezpiecznie przedostać się na drugi brzeg?
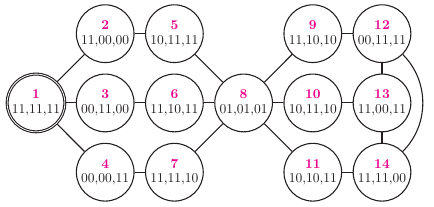
Rys. 3 Opis stanu: pary bitów oddzielone przecinkami opisują kolejne rodzeństwa; pierwszy bit określa obecność brata, drugi - siostry; cykl nieparzystej długości: 1, 3, 6, 8, 10, 13, 12, 14, 13, 10, 8, 6, 3, 1 (13 krawędzi).
Więcej o zagadkach ze zbioru zadań napisanego przez błogosławionego Alkuina z Yorku
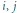 oznacza
oznacza 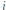 dorosłych oraz j dzieci; cykl nieparzystej długości: 3, 4, 5, 6, 7, 7, 6, 5, 4, 3 (9 krawędzi).
dorosłych oraz j dzieci; cykl nieparzystej długości: 3, 4, 5, 6, 7, 7, 6, 5, 4, 3 (9 krawędzi).