Grą tą będą dzielniki, w które gra się następująco: na początku na tablicy mamy wypisane pewne liczby. Dwaj gracze na przemian wykonują ruchy. Ruch polega na wybraniu nieskreślonej liczby z tablicy i skreśleniu jej wraz ze wszystkimi jej dzielnikami. Ten, kto nie może się ruszyć, przegrywa. Jak widać, gra jest bez elementów losowych i rozstrzyga się w czasie skończonym. Dzięki temu wiemy, że któryś z graczy ma strategię wygrywającą. Teraz czas na właściwe pytanie: rozważmy grę w dzielniki na zbiorze liczb od 1 do 100. Który z graczy ma wówczas strategię wygrywającą?

Jak należy w tę grę grać, żeby wygrać? Nie wiemy... i nie musimy wiedzieć! Przy pytaniu o wygraną interesuje nas "kto" wygra, a nie "jak". I odpowiemy na to pytanie dzięki następującemu spostrzeżeniu: liczba 1 pełni w tej grze osobliwą rolę - na pewno zostanie skreślona w pierwszym ruchu. Zanim z tego skorzystamy, rozpatrzmy grę w dzielniki na zbiorze liczb od 2 do 100. Który gracz wygrywa w drugiej grze?

Załóżmy wpierw, że strategię wygrywającą ma wtedy gracz rozpoczynający. W pierwszym ruchu wybiera liczbę 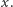W takim razie w pierwszej grze również wygrywa gracz rozpoczynający, w pierwszym ruchu skreślając 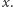Potem wykonuje ruchy jak w grze w dzielniki od 2 do 100, bo to już ta sama gra, w końcu jedynki nie można wybrać.

Załóżmy teraz, że gracz drugi ma strategię wygrywającą w grze "od dwójki". Wtedy grając w grę "od jedynki", w pierwszej turze skreślamy 1 i od tego momentu zachowujemy się jak gracz drugi w grze "od dwójki"..., kradnąc jego strategię i tym samym wygrywając. Oznacza to, że w grze "od jedynki" gracz rozpoczynający może wygrywać zawsze. Ale jak? Nie wiemy i tym sposobem, niestety, się nie dowiemy...