Alfred podszedł z zaciekawieniem do kolejnego odkrycia, a Berenika, zauważywszy, że coś tam ma, w mig znalazła się obok niego.
- Co w nim jest? - zapytała podekscytowana znaleziskiem. - Rozwiąż!
Chłopiec otworzył worek, a sznurek włożył do kieszeni. W środku znaleźli mnóstwo starych monet. Alfred wyjął kilka z nich i przyglądał się im z uwagą.
- Wyglądają na stare, jeszcze sprzed denominacji. Raczej nie są warte za wiele. Trudno oszacować, ile ich może być. Setka, może więcej. Jak sądzisz?
Po parokrotnym zanurzeniu dłoni w zawartości woreczka dziewczynka orzekła:
- Więcej niż setka. Jak zwykle, dzielimy sprawiedliwie, żeby każdy był zadowolony.
- Sprawiedliwie… Czyli tym razem jak? - dzielenie się zdobyczą przerabiali już parokrotnie na różne sposoby.
- Mam nowy pomysł! Możemy wprowadzić do naszego podziału nutkę losowości. Proponuję, byśmy nie wysypywali zawartości. Nie będziemy wiedzieli, co i ile tak naprawdę dzielimy. - To wrzućmy do tego zmiętego i mokrego worka monety, które wyjęliśmy i na zmianę losowo wyjmujmy po jednej. Możesz zaczynać - podchwycił pomysł Alfred.
- Dzięki, ale myślę że lepiej będzie, gdy wyciągniemy tymczasowo jedną monetę i będziemy nią rzucać. Jeżeli wypadnie orzeł, ja wyciągam jedną monetę, w przeciwnym przypadku ty.

Alfred i Berenika długo dyskutowali, czyj sposób losowania jest lepszy.

Opisany powyżej problem jest wariantem zagadnienia sprawiedliwego podziału. W tym przypadku nie wiemy jednak, jaka jest całkowita wartość rzeczy dzielonej, ani ile wyborów czeka bohaterów. W szczególności nie wiemy, czy monet jest parzyście, czy nieparzyście wiele. Moglibyśmy posłużyć się zasadą "ja dzielę, Ty wybieraj", ale Alfred i Berenika chcą dzielić znalezisko przed określeniem jego całkowitej wartości, której zresztą sami nie potrafią, a może nie chcą określić.

Przyjrzyjmy się bliżej zaproponowanym przez nich sposobom. Czy któryś z nich jest sprawiedliwy? Jeżeli tak, dlaczego? A jeżeli nie, to który jest sprawiedliwszy? Co powinni zrobić, by zagwarantować równość?

W propozycji Bereniki rzut monetą oznacza, że możemy jedynie oczekiwać, że podział zakończy się zbliżoną liczbą monet u każdego. Niemniej, przy tym sposobie zarówno Alfred, jak i Berenika mają duże szanse na to, żeby skończyć z przewagą co najmniej kilku, a nawet kilkunastu monet - co drugiej stronie może się ewidentnie nie spodobać. Wartość monet nie ma w tym przypadku znaczenia, gdyż jest niewielka. Problem sprowadzamy do tego, żeby oboje zakończyli podział z taką samą liczbą monet, albo żeby w dowolnym momencie każde z nich miało równe szanse na zakończenie podziału z większą liczbą. Ciekawa propozycja Bereniki nie jest najlepszym rozwiązaniem. Jest bowiem duża szansa, że gdy jedna osoba zdobędzie przewagę kilku monet, to utrzyma ją już do końca.

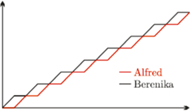
Podział monet wg Alfreda

Propozycja Alfreda polega na naprzemiennym wyjmowaniu po jednej monecie. Jeżeli liczba monet jest parzysta, oboje skończą z taką samą ich liczbą. W przeciwnym przypadku, gdy monet jest nieparzyście wiele, Berenika będzie miała o jedną monetę więcej. Taki podział nigdy nie stawia Alfreda na pozycji lidera (przypomnijmy: ustaliliśmy już, że to, co znajduje się na monecie, nie ma znaczenia). Oznacza to, że średnio albo oboje będą mieli tyle samo, albo Berenika więcej. Podział faworyzuje więc (nieznacznie) Berenikę. Algorytm wydaje się jednak nieco lepszy od propozycji Bereniki. Istotnie, nie polegamy już na losowości, niemniej można go poprawić tak, by uzyskać jeszcze "sprawiedliwszy" podział. Propozycję Alfreda możemy obrazowo zapisać w postaci ciągu par

gdzie pozycja litery od lewej oznacza numer losowania, a litera, która z dwóch osób wyciąga w danej turze monetę. Problem tego ciągu tkwi w tym, iż każda nieparzysta pozycja zajmowana jest przez 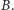Możemy go uniknąć i tym samym poprawić ciąg podziału, gdy w co drugiej parze litery zamienimy miejscami (grupujemy teraz w czwórki takich samych symboli)

Taki podział, choć jest lepszy od poprzedniego, ponownie nie jest idealny. Na czym polega jego przewaga? Jeżeli przedmiotów podziału jest parzyście wiele, to Berenika nie jest już zawsze faworyzowana. W powyższym ustawieniu 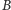i 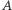występują na nieparzystych miejscach naprzemiennie. Z drugiej strony, niezależnie od liczby monet, ciąg liderów wygląda następująco

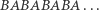
Po pierwszym losowaniu liderem jest 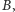po drugim lidera nie ma (obydwoje mają taką samą liczbę monet), po trzecim liderem jest 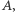po czwartym lidera nie ma, po piątym liderem jest 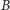itd. Podział taki jako lidera faworyzuje więc ponownie Berenikę, gdyż ta zawsze będzie liderem co najmniej tyle samo razy co Alfred. Alfred może mieć więc (słuszne) pretensje. W obecnym algorytmie podziału czwórka 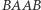powtarza się i ta cykliczność jest źródłem problemu. Zauważmy, że w pierwotnym podziale ciąg również był okresowy (powtarzał się segment 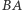). Sugeruje to, podobnie jak poprzednio, zamianę w co drugiej czwórce symboli na przeciwne. Generuje to ciąg okresowy, w którym powtarza się cyklicznie osiem symboli:

Analiza liderów prowadzi do ciągu

Ale jest to ciąg, w którym, jak już ustaliliśmy, faworyzowana jest Berenika. Cykliczność, tym razem 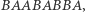ponownie prowadzi do niesprawiedliwości, lecz na nieco głębszym poziomie.

Możemy spróbować przejść do ogólnych wniosków. Po każdej z powyższych zmian ciąg podziału jest okresowy, co przekłada się ostatecznie na okresowość któregoś skumulowania (tworzymy ciąg liderów od ciągu liderów), a tym samym faworyzowanie Bereniki. Kolejne korekty dokonujemy w co drugiej parze, czwórce, ósemce 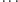- ogólniej, w co drugiej 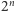-tce przez zamianę symboli. Ponieważ nie znamy dokładnej liczby monet, a chcielibyśmy zaproponować maksymalnie sprawiedliwy sposób losowania, sugeruje to wykonanie na nieskończonym ciągu nieskończenie wielu operacji zamiany liter. Operacja taka ma swoją "granicę", której początek wygląda następująco

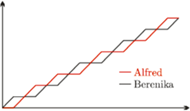
Podział monet wg Thuego-Morse'a

Powyższy ciąg można skonstruować również w inny sposób. Startujemy mianowicie od pary liter 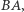do której po prawej stronie dołączamy jej negatyw, czyli ciąg liter, w którym 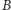i 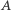zamienione zostały miejscami. Następnie do otrzymanego ciągu 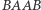dołączamy kolejny negatyw, otrzymując 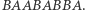Operację taką powtarzamy w nieskończoność, otrzymując w granicy to samo co poprzednio. Ciąg ten nosi nazwę ciągu Thuego-Morse'a i czasem jest nazywany ciągiem sprawiedliwego podziału (fair share sequence). Taką nazwę zawdzięcza zastosowaniu do rozwiązania problemu, z którym Alfred i Berenika borykali się na gdańskiej plaży. Jego "doskonałość" polega między innymi na tym, że ciąg liderów jest ponownie ciągiem Thuego-Morse'a, a więc i wszystkie kolejne iteracje skumulowanego prowadzenia są tej postaci.

- Ciąg Thuego-Morse'a? Nigdy o nim nie słyszałem! - skarży się Alfred.
Berenika była wyraźnie zaskoczona tym, co przeczytali w znanym czasopiśmie popularnonaukowym. Interesowała się matematyką, o ciągu Thuego-Morse'a przeczytała parę faktów przed miesiącem, ale żaden z nich nie dotyczył sprawiedliwego podziału.
- Nie przejmuj się, Alfredzie! Nie tylko udało nam się podzielić monety najsprawiedliwiej. Poznaliśmy również ciąg sprawiedliwego podziału. Poczekaj chwilę... Tutaj jest napisane, że to właśnie zgodnie z tą regułą piłkarze powinni rozgrywać rzuty karne w dogrywce, szachiści zmieniać się kolorami pionów w rozgrywkach, czy tenisiści serwować w tie-breaku. Wyeliminowałoby to problem przewagi osoby rozpoczynającej, dając tym samym sprawiedliwszą rozgrywkę. Zdumiewające!

A gdyby przydarzyło Ci się, drogi Czytelniku, spacerować po plaży razem z Alfredem i Bereniką, jaki sprawiedliwy ciąg losowań zaproponowałbyś dla trzech osób?