Mała Delta
Nowości z przeszłości
Spór na rynku w Babilonie
Na rynku w Babilonie dwóch kupców, Nabonit i Enkidu, sprzedawało swoje towary. Łączyła ich wielka przyjaźń, ale też przy lada okazji lubili się sprzeczać i kłócić. Ostatnio powstał między nimi spór o sposób ważenia towarów...

Obaj przyjaciele ważyli, kładąc na jednej szalce wagi odważniki, a na drugiej towary. Enkidu używał czterech odważników, Nabonit również czterech, ale odważniki Enkidu różniły się od odważników Nabonita ciężarem. Enkidu używał następujących odważników: jeden o ciężarze 1 miny (mina to jednostka ciężaru na rynku w Babilonie), dwa odważniki po 2 miny i jeden o ciężarze 5 min. Natomiast Nabonit posługiwał się odważnikami o ciężarach: 1 mina, 2 miny, 5 min, 10 min.
- Mój komplet odważników jest lepszy - twierdził Nabonit - bo moimi odważnikami mogę odważyć nawet 18 min, a ty swoimi odważnikami zważysz najwyżej 10 min.
- Masz rację - odpowiedział Enkidu - ale ja zważę swoimi odważnikami każdy towar o ciężarze od 1 do 10 min. Jeśli mam zważyć większą ilość towaru, odważam je najpierw porcjami po dziesięć min, a na końcu resztę. Natomiast ty swoimi odważnikami nie potrafisz zważyć ani 4, ani 9 min!

Ich spór trwałby zapewne aż do dzisiaj, gdyby w końcu nie zdecydowali, że pójdą do biblioteki, pełnej bardzo mądrych glinianych tabliczek o matematyce (w owym czasie nie znano jeszcze książek) i spróbują dowiedzieć się z nich, jaki jest najlepszy sposób ważenia. Siedzieli w bibliotece codziennie przez cały tydzień, czytając bardzo ciekawe tabliczki, a kiedy wrócili na rynek do swoich kramów, wyrzucili zaraz stare odważniki i zastąpili je nowymi.
- Nikt na całym rynku w Babilonie nie ma teraz lepszego kompletu odważników niż my - chwalili się głośno obaj przyjaciele.
Ponieważ o ich sporze słyszeli już niemal wszyscy w Babilonie, znalazło się wielu ciekawych, którzy chcieli się dowiedzieć, czego Nabonit i Enkidu nauczyli się, siedząc cały tydzień w bibliotece, i jak wygląda ich słynny komplet odważników. Nasi kupcy z wielką ochotą tłumaczyli wszystkim ciekawym, na czym polega nowy sposób ważenia.
- Chcieliśmy dobrać cztery takie odważniki, żeby za ich pomocą można było zważyć każdą ilość towaru, i to od jednej miny aż do tylu, jak tylko jest to możliwe. Możliwości odważenia różnych ciężarów jest tyle, ile różnych zestawów da się ułożyć z czterech odważników. Uczyliśmy się matematyki cały tydzień i teraz już wiemy, że z czterech odważników da się ułożyć tylko 15 różnych zestawów przydatnych do ważenia, o czym zaraz wszystkich przekonamy. Oznaczmy cztery odważniki (nie wiemy jeszcze, po ile min mają one ważyć) czterema literami 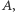
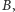
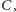
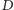 i ustawmy je w pewnej kolejności. Najwygodniej nam będzie ustawić je tak:
i ustawmy je w pewnej kolejności. Najwygodniej nam będzie ustawić je tak: 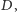
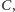
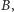
 Będziemy teraz układali wszystkie możliwe zestawy tych odważników i rysowali je na specjalnym "matematycznym drzewku".
Będziemy teraz układali wszystkie możliwe zestawy tych odważników i rysowali je na specjalnym "matematycznym drzewku".
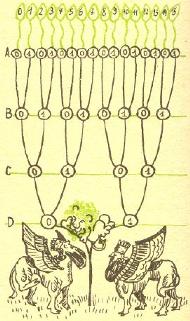
Tu Enkidu narysował na piasku "matematyczne drzewko" - takie, jakie na rysunku obok.
- Każda gałąź drzewka oznacza jeden z możliwych zestawów odważników - objaśnia Enkidu sporemu tłumowi ciekawych. - Idąc po drzewku od podstawy do jednego z wierzchołków ponumerowanych liczbami od zera do piętnastu, przecinamy po drodze cztery linie: 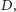
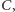
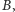
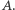 Zestaw odważników układamy następująco: jeśli na linii
Zestaw odważników układamy następująco: jeśli na linii 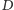 spotkamy po drodze zero to do zestawu nie dobieramy odważnika oznaczonego literą
spotkamy po drodze zero to do zestawu nie dobieramy odważnika oznaczonego literą 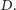 Ale jeśli spotkamy jedynkę, wówczas włączamy ten odważnik do zestawu. Podobnie będziemy postępować na liniach
Ale jeśli spotkamy jedynkę, wówczas włączamy ten odważnik do zestawu. Podobnie będziemy postępować na liniach 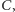
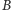 i
i 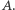 Na przykład po drodze, która kończy się wierzchołkiem oznaczonym numerem 11, napotykamy kolejno: na linii
Na przykład po drodze, która kończy się wierzchołkiem oznaczonym numerem 11, napotykamy kolejno: na linii 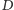 jedynkę (bierzemy odważnik
jedynkę (bierzemy odważnik 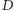 ), na linii
), na linii 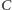 zero (nie bierzemy odważnika
zero (nie bierzemy odważnika 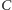 ), na linii
), na linii 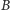 jedynkę (bierzemy odważnik
jedynkę (bierzemy odważnik 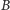 ) i na linii
) i na linii 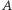 jedynkę (bierzemy odważnik
jedynkę (bierzemy odważnik 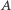 ). Przebytą drogę można zapisać: 1011. Zapis ten oznacza, że zestaw jedenasty składa się z odważników
). Przebytą drogę można zapisać: 1011. Zapis ten oznacza, że zestaw jedenasty składa się z odważników 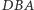 (nie ma w nim jedynie odważnika
(nie ma w nim jedynie odważnika 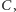 bo tylko na drugim miejscu w tym zapisie jest zero). (Tłumacz wie o tym, że Babilończycy zera nie znali - ale Czytelnicy przecież zero znają).
bo tylko na drugim miejscu w tym zapisie jest zero). (Tłumacz wie o tym, że Babilończycy zera nie znali - ale Czytelnicy przecież zero znają).
- Przechodząc od linii do linii zawsze napotykamy rozwidlenie dróg. Jedna z dróg rozwidlenia prowadzi do jedynki, a druga do zera. Oznacza to, że do jednego z zestawów będziemy brali kolejny odważnik, a do drugiego nie. Są to już wszystkie możliwości. A więc wszystkich zestawów jest dokładnie tyle, ile ma gałęzi "matematyczne drzewko". Tylko jedna z gałęzi nie przyda się do ważenia, tj. ta, która się kończy w wierzchołku oznaczonym zerem. Idąc drogą do wierzchołka zerowego nie weźmiemy do zestawu żadnego odważnika, niczego więc takim zestawem nie zważymy. W pozostałych zestawach jest zawsze przynajmniej jeden odważnik i nie ma zestawów takich samych. A więc możliwości zważenia różnych ciężarów jest dokładnie 15 - zakończył objaśnienia Enkidu. Z kolei Nabonit pokazał wszystkim ciekawym nowy komplet odważników.
- Jest to najlepszy ze wszystkich możliwych kompletów czterech odważników - powiedział Nabonit. Można nim zważyć każdą ilość towaru o ciężarze od 1 do 15 min! Czy może być lepszy komplet odważników?

Czy domyślacie się, jak wygląda ten nadzwyczajny komplet? Jeśli nie udało się Wam go jeszcze dobrać, a jesteście ciekawi, jakie odważniki dobrali do swojego kompletu nasi przyjaciele, zdradzimy Wam jego tajemnicę. A więc odważniki 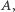
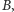
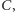
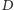 powinny ważyć kolejno 1, 2, 4 i 8 min (każdy następny dwa razy tyle, co poprzedni). Spróbujcie przy pomocy tego kompletu odważyć 11 min towaru i inne jeszcze ilości, a potem popatrzcie jeszcze raz na "matematyczne drzewko" kupców z Babilonu i sprawdźcie, ile będą ważyły odważniki każdego z zestawów, które otrzymamy idąc po drzewku szesnastoma różnymi drogami. Czy zauważyliście coś ciekawego?
powinny ważyć kolejno 1, 2, 4 i 8 min (każdy następny dwa razy tyle, co poprzedni). Spróbujcie przy pomocy tego kompletu odważyć 11 min towaru i inne jeszcze ilości, a potem popatrzcie jeszcze raz na "matematyczne drzewko" kupców z Babilonu i sprawdźcie, ile będą ważyły odważniki każdego z zestawów, które otrzymamy idąc po drzewku szesnastoma różnymi drogami. Czy zauważyliście coś ciekawego?
Powróćmy jednak do naszych przyjaciół z Babilonu. Pamiętacie, że Nabonit powiedział: Ćzy może być lepszy komplet odważników?". Przekonaliście się chyba, że przy takiej metodzie ważenia, jaką się posługują nasi kupcy, lepszego sposobu nie ma. Ale Nabonit nie wziął pod uwagę, że używając wagi szalkowej, można kłaść odważniki na obie szalki. A przy takim sposobie ważenia można dobrać znacznie lepszy komplet od tego, jakim się posługują Nabonit i Enkidu. Odważniki 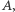
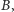
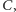
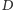 tego znacznie lepszego kompletu powinny ważyć kolejno: 1, 3, 9 i 27 min. Da się nimi zważyć każdą ilość towaru od jednej miny aż do czterdziestu! Na przykład dwadzieścia min można zważyć, kładąc na jedną szalkę odważniki: 27 i 3 miny, a na drugą szalkę, wraz z ważonym towarem, odważniki 9 min i 1 minę. Spróbujcie tymi odważnikami odważyć jeszcze inne ilości towaru. Czy do takiego sposobu ważenia umiecie narysować "matematyczne drzewko" podobne do tego, które narysował Enkidu? Spróbujcie! Bądźcie tylko przygotowani na to, że drzewko będzie miało wówczas aż 81 gałęzi, ale tylko czterdzieści z nich przyda się do ważenia (dlaczego?). Pamiętajcie też, że na każdej linii każda gałąź musi rozwidlać się na trzy odnogi. Jedną z nich oznaczcie znakiem minus (będzie to oznaczało, że kładziemy odważnik na szalkę, na której znajduje się towar). Drugą oznaczcie zerem (nie kładziemy odważnika na żadną szalkę) i wreszcie trzecią oznaczcie znakiem plus (kładziemy odważnik na szalkę dla odważników). Innych możliwości już nie ma, a więc i to drzewko będzie wskazywało wszystkie możliwe układy odważników na szalkach.
tego znacznie lepszego kompletu powinny ważyć kolejno: 1, 3, 9 i 27 min. Da się nimi zważyć każdą ilość towaru od jednej miny aż do czterdziestu! Na przykład dwadzieścia min można zważyć, kładąc na jedną szalkę odważniki: 27 i 3 miny, a na drugą szalkę, wraz z ważonym towarem, odważniki 9 min i 1 minę. Spróbujcie tymi odważnikami odważyć jeszcze inne ilości towaru. Czy do takiego sposobu ważenia umiecie narysować "matematyczne drzewko" podobne do tego, które narysował Enkidu? Spróbujcie! Bądźcie tylko przygotowani na to, że drzewko będzie miało wówczas aż 81 gałęzi, ale tylko czterdzieści z nich przyda się do ważenia (dlaczego?). Pamiętajcie też, że na każdej linii każda gałąź musi rozwidlać się na trzy odnogi. Jedną z nich oznaczcie znakiem minus (będzie to oznaczało, że kładziemy odważnik na szalkę, na której znajduje się towar). Drugą oznaczcie zerem (nie kładziemy odważnika na żadną szalkę) i wreszcie trzecią oznaczcie znakiem plus (kładziemy odważnik na szalkę dla odważników). Innych możliwości już nie ma, a więc i to drzewko będzie wskazywało wszystkie możliwe układy odważników na szalkach.

Można dobierać także inne komplety odważników odpowiednio do różnych sposobów ważenia. Na przykład przy pomocy 18 odważników - dziewięciu odważników "mniejszych" 1, 2, 3, 4, 5, 6, 7, 8, 9 min oraz dziewięciu odważników "większych" 10, 20, 30, 40, 50, 60, 70, 80, 90 min - można zważyć każdą ilość towaru: od 1 do 99 min, i to z zachowaniem warunku, że odważniki kładziemy tylko na jednej szalce, przy czym na szalce znajduje się najwyżej jeden odważnik "mniejszy" i jeden "większy". Czy wiecie, jak tą metodą zważyć 78 min towaru? Proste, prawda?
Jeśli proste, to weźcie teraz 8 następujących odważników: 4 odważniki "mniejsze" 1, 2, 3 i 4 miny oraz 4 odważniki "większe" 5, 10, 15 i 20 min. Jakie ciężary można nimi odważać, zachowując opisane wyżej warunki (na szalce kładziemy jeden odważnik "mniejszy" i jeden odważnik "większy")? Do ważenia tymi odważnikami posłużcie się tabelką, którą narysowaliśmy poniżej. Pokazuje ona, jak układać z odważników wszystkie możliwe ciężary.
Czy umiecie obmyślić jeszcze inne podobne komplety odważników? A czy potrafilibyście ułożyć komplet odważników do ważenia przy możliwości umieszczania na szalce najwyżej trzech odważników: jednego "małego", jednego "średniego" i jednego "większego"?
Jeśli zainteresowały Was różne metody ważenia i chcecie wiedzieć o nich coś więcej, zainteresujcie się działem matematyki, który mówi o niedziesiątkowych systemach pozycyjnych!