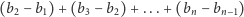Mała Delta

Architekci i algorytmy

W pewnym mieście podjęto decyzję o budowie nowego osiedla. Postanowiono, że będzie to szereg ośmiu budynków. Przyjęto, że żadne trzy stojące obok siebie budynki nie mogą być tej samej wysokości. Ustalono, że budynki będą mieć wysokości równe odpowiednio: 5, 10, 10, 15, 25, 25, 30 i 45 metrów...

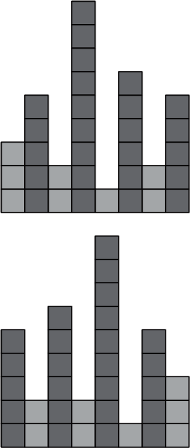
Pojawiło się pytanie:

Jak należy uszeregować budynki, aby widok osiedla z pewnej odległości był jak najładniejszy?

Zdania na ten temat wśród miejscowych architektów były podzielone. Ogłoszono konkurs na projekt osiedla. Dwie pracownie architektoniczne, znajdujące się w tym mieście, przedstawiły swoje projekty urbanistyczne.

Pierwsza grupa architektów, bardziej tradycyjna, zaproponowała, by trzymać się zasady, że należy minimalizować sumę różnic wysokości sąsiadujących ze sobą budynków. Ich zdaniem oznaczało to tyle, że budynki należy uszeregować od najniższego do najwyższego (lub w odwrotnej kolejności).

Druga pracownia, bardziej nowoczesna, uważała inaczej - architekci uznali, że sąsiednie budynki powinny różnić się co do wysokości najbardziej, jak to jest tylko możliwe (czyli suma różnic wysokości sąsiadujących ze sobą budynków powinna być jak największa). Co zaskakujące, do projektu druga grupa architektów dołączyła aż dwa rysunki (plany) osiedla, które ich zdaniem stanowiły przykłady optymalnych rozwiązań. Algorytmu, który zastosowali do ich znalezienia, pracownia jednak nie ujawniła.

Po burzliwej dyskusji jury konkursu ostatecznie zdecydowało, że zwycięży drugi projekt drugiej grupy architektów.

Warto zastanowić się, czy grupy architektów miały rację? To znaczy: Czy algorytmy, jakie zastosowano, rzeczywiście dawały najlepsze z możliwych (optymalne) rozwiązania dla różnych dla obu grup specyfikacji problemu?

Przeanalizujmy propozycję pierwszej grupy.

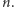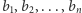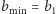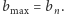Załóżmy, że budynków jest $|n.$ Niech $b1,b2,...,bn$ to wysokości budynków uszeregowanych od najniższego do najwyższego. Oznaczmy dodatkowo $|bmin = b1$ i $|bmax = bn.$ W przypadku takiego uszeregowania otrzymamy sumę różnic wysokości równą 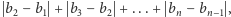$| b2 −b1 + b3 − b2 +...+ bn− bn−1 ,$ którą, oczywiście, możemy zastąpić sumą

(b − b )+ (b − b ) +...+ (b −b ) = b − b = b − b . 2 1 3 2 n n− 1 n 1 max min

Zauważmy, że nie sposób uszeregować budynki tak, aby suma różnic wysokości sąsiednich budynków była mniejsza niż różnica wysokości najwyższego i najniższego. Inaczej mówiąc - w przypadku każdego innego uszeregowania poszukiwana suma różnic wysokości będzie większa od różnicy 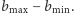$|b − b . max min$ Dlaczego? W zrozumieniu tej prawidłowości może pomóc interpretacja geometryczna - poszukiwana suma jest sumą długości odcinków o długościach równych odpowiednim różnicom wysokości sąsiednich budynków. Oczywiście, suma mnogościowa tych odcinków jest równa odcinkowi o długości $b − b . max min$

Podsumowując - pierwsza grupa architektów przedstawiła optymalne rozwiązanie (dla ich specyfikacji problemu).

Co możemy powiedzieć o rozwiązaniu (rozwiązaniach) drugiej grupy? Czy ktoś z Czytelników potrafi sformułować algorytmy, jakimi posługiwali się architekci w celu otrzymania rozwiązań? Czy te algorytmy dają optymalne rozwiązanie dla ich specyfikacji problemu? Odpowiedź na drugie pytanie wydaje się nie być wcale taka prosta.