Gra Grim i twierdzenie Sprague’a–Grundy’ego
Pewnie część czytelników Delty zna grę Nim – zarówno jej zasady, jak i właściwą dla niej strategię wygrywającą. W tym artykule chcemy przedstawić inną grę grafową. Grę o prostych zasadach, ale trudniejszą niż Nim do dokładnego przeanalizowania. Tą grą jest – stworzony przez Jamie Peabody i Karen Willis – Grim. Podamy efektywny sposób orzekania, który gracz ma strategię wygrywającą. Co najciekawsze, można go zastosować do szerokiej klasy tego typu gier dwuosobowych, zawierającej Grima i Nima.

Rys. 1 Graf, który określamy mianem „łańcucha”. W tym przypadku jest to łańcuch długości 8.
W Grimie dwaj uczestnicy naprzemiennie wykonują ruchy. Na początku rozgrywki mają oni do dyspozycji pewien graf. W tym artykule będziemy rozważać jedynie grafy początkowe, które są „łańcuchami”, tzn. takie grafy spójne, w których dwa wierzchołki mają stopień 1, a reszta wierzchołków ma stopień 2 (taki graf pokazany jest na rysunku 1).
W każdym ruchu gracz wybiera dowolny nieizolowany wierzchołek grafu i usuwa go wraz ze wszystkimi krawędziami z niego wychodzącymi. Przegrywa gracz, który jako pierwszy nie może wykonać ruchu.

Rys. 2 Przykładowa rozgrywka dla nieparzystej liczby wierzchołków przy założeniu, że gracz pierwszy gra zgodnie z opisaną w artykule strategią wygrywającą.
Jeśli liczba wierzchołków grafu jest nieparzysta (oczywiście, większa od 1), to istnieje strategia wygrywająca dla gracza pierwszego – wystarczy jako pierwszy wierzchołek wybrać wierzchołek będący środkiem symetrii, a następnie odbijać ruchy przeciwnika względem środka (Rys. 2). Po każdym ruchu pierwszego gracza, postępującego zgodnie z opisanym tu algorytmem, pozostałe wierzchołki są ponownie symetryczne względem środka. Dopóki drugi gracz jest w stanie wykonać ruch, dopóty pierwszy gracz może rozpocząć następną kolejkę. Zatem drugi gracz nie może wykonać dozwolonego ruchu jako ostatni. Ponieważ wierzchołków jest skończenie wiele, gra musi zakończyć się jego przegraną.
Trudniejszy do rozważenia jest przypadek, gdy liczba wierzchołków jest parzysta. Gdy wynosi ona 2, to strategię wygrywającą ma gracz pierwszy – niezależnie od wykonanego ruchu, drugiemu graczowi pozostanie jedynie izolowany wierzchołek. Dla czterech wierzchołków strategię wygrywającą ma gracz drugi. Dla łańcucha długości 6, 8 lub 10 znów wygrywa gracz pierwszy, ale dla długości 12 – drugi. Można tego dowieść, rozrysowując drzewo gry, niestety, o wykładniczej zależności liczby węzłów od długości łańcucha. Co dalej? Z pomocą przychodzi nam komputer i twierdzenie Sprague’a–Grundy’ego. Żeby je przedstawić, wprowadzimy najpierw kilka pojęć.
Grę nazwiemy normalną, jeśli przegrywa w niej ten z graczy, który jako pierwszy nie jest w stanie wykonać ruchu. Będziemy mówić, że gra jest bezstronna, jeśli obaj gracze mogą wykonać te same ruchy, mając do dyspozycji daną planszę. Przykładowo gra w kółko i krzyżyk bezstronna nie jest, gdyż gracz stawiający kółko nie może postawić krzyżyka. Grim i Nim zaliczają się do gier bezstronnych.
Funkcja mex (ang. minimum excludant) przyporządkowuje podzbiorowi zbioru liczb naturalnych najmniejszą liczbę naturalną do niego nienależącą. Na przykład,

Funkcja Sprague’a–Grundy’ego
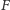 określona jest rekurencyjnie dla
poszczególnych pozycji w grze. Dla konfiguracji
określona jest rekurencyjnie dla
poszczególnych pozycji w grze. Dla konfiguracji
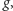 w której gracz
nie jest w stanie wykonać ruchu, definiujemy
w której gracz
nie jest w stanie wykonać ruchu, definiujemy
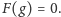 Dla innych
pozycji funkcja ta zwraca
Dla innych
pozycji funkcja ta zwraca
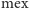 zbioru wartości
zbioru wartości
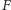 dla
wszystkich pozycji
dla
wszystkich pozycji
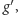 do których możemy dojść w jednym
ruchu z
do których możemy dojść w jednym
ruchu z
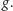 Do poprawności definicji
Do poprawności definicji
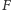 wystarczy acykliczność
gry, czyli brak możliwości powtórzenia konfiguracji w czasie rozgrywki, oraz
założenie, że dla każdej konfiguracji początkowej gra może potrwać
co najwyżej skończenie wiele tur.
wystarczy acykliczność
gry, czyli brak możliwości powtórzenia konfiguracji w czasie rozgrywki, oraz
założenie, że dla każdej konfiguracji początkowej gra może potrwać
co najwyżej skończenie wiele tur.
W grze Grim dla pozycji składającej się z jednego bądź kilku
izolowanych wierzchołków nie ma możliwości wykonania ruchu, więc
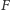 przyjmuje wartość
przyjmuje wartość
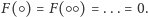 Łańcuchowi
długości 2 funkcja
Łańcuchowi
długości 2 funkcja
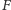 przyporządkowuje
przyporządkowuje
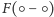 równe
równe
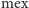 z wartości
z wartości
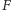 dla wierzchołka izolowanego, który
uzyskujemy niezależnie od tego, na który z dwóch możliwych ruchów
się zdecydujemy. Zatem
dla wierzchołka izolowanego, który
uzyskujemy niezależnie od tego, na który z dwóch możliwych ruchów
się zdecydujemy. Zatem
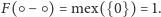 Wartość
Wartość
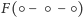 równa jest natomiast wartości funkcji
równa jest natomiast wartości funkcji
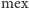 dla zbioru
zawierającego: wartość
dla zbioru
zawierającego: wartość
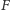 dla dwóch izolowanych wierzchołków
dla dwóch izolowanych wierzchołków
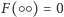 oraz dla łańcucha długości 2,
oraz dla łańcucha długości 2,
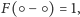 a zatem
a zatem
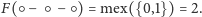
Nim-suma to pewne działanie
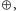 które dwóm liczbom naturalnym
przyporządkowuje również liczbę naturalną. Aby obliczyć Nim-sumę, należy
zapisać oba argumenty w systemie dwójkowym, dodać liczby stojące przy
tych samych potęgach dwójki (a więc zera lub jedynki) modulo 2, a następnie
wynik zinterpretować jako zapis dwójkowy szukanej liczby. Z powyższego
przepisu wynika od razu, że
które dwóm liczbom naturalnym
przyporządkowuje również liczbę naturalną. Aby obliczyć Nim-sumę, należy
zapisać oba argumenty w systemie dwójkowym, dodać liczby stojące przy
tych samych potęgach dwójki (a więc zera lub jedynki) modulo 2, a następnie
wynik zinterpretować jako zapis dwójkowy szukanej liczby. Z powyższego
przepisu wynika od razu, że
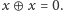
Twierdzenie Sprague’a–Grundy’ego pozwala wyznaczyć wartości
funkcji
 w sytuacji, gdy gracze grają w kilka normalnych i bezstronnych
gier jednocześnie: w każdym ruchu wybierają jedną z plansz i wykonują
na niej ruch zgodnie z zasadami odpowiadającej jej gry. Tak powstałą
„multigrę” nazywamy sumą gier.
w sytuacji, gdy gracze grają w kilka normalnych i bezstronnych
gier jednocześnie: w każdym ruchu wybierają jedną z plansz i wykonują
na niej ruch zgodnie z zasadami odpowiadającej jej gry. Tak powstałą
„multigrę” nazywamy sumą gier.
Twierdzenie 1 (Sprague–Grundy).
Funkcja Sprague’a–Grundy’ego
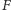 dla sumy normalnych, bezstronnych
gier jest równa Nim-sumie funkcji Sprague’a–Grundy’ego poszczególnych
gier. Gracz wykonujący ruch ma strategię wygrywającą wtedy i tylko wtedy,
gdy wartość funkcji
dla sumy normalnych, bezstronnych
gier jest równa Nim-sumie funkcji Sprague’a–Grundy’ego poszczególnych
gier. Gracz wykonujący ruch ma strategię wygrywającą wtedy i tylko wtedy,
gdy wartość funkcji
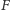 dla aktualnej pozycji gry jest niezerowa.
dla aktualnej pozycji gry jest niezerowa.
W przypadku, gdy funkcja
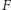 dla pozycji gry
dla pozycji gry
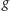 przyjmuje
wartość
przyjmuje
wartość
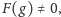 możliwy jest ruch do takiej pozycji
możliwy jest ruch do takiej pozycji
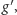 by
by
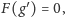 zgodnie z definicją funkcji
zgodnie z definicją funkcji
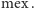 Pozycja
Pozycja
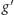 może
kończyć grę (dla takich
może
kończyć grę (dla takich
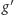 z definicji
z definicji
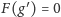 ), choć nie musi.
Jeżeli
), choć nie musi.
Jeżeli
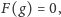 to wówczas dla każdej pozycji
to wówczas dla każdej pozycji
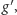 osiągalnej
za pomocą jednego ruchu, mamy
osiągalnej
za pomocą jednego ruchu, mamy
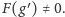 Strategia wygrywająca
polega na takim wykonywaniu ruchów, by po każdym z nich trafić do takiej
pozycji
Strategia wygrywająca
polega na takim wykonywaniu ruchów, by po każdym z nich trafić do takiej
pozycji
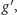 że
że
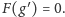
Jako przykład zastosowania rozważmy sumę dwóch egzemplarzy pewnej gry
bezstronnej i normalnej (gramy tymi samymi zasadami, rozpoczynamy
z tą samą pozycją początkową
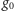 na obu planszach). Wygrywa ten
z graczy, który jako ostatni jest w stanie wykonać ruch. Na mocy podanego
twierdzenia wartość funkcji Sprague’a–Grundy’ego dla tak powstałej gry będzie
równa
na obu planszach). Wygrywa ten
z graczy, który jako ostatni jest w stanie wykonać ruch. Na mocy podanego
twierdzenia wartość funkcji Sprague’a–Grundy’ego dla tak powstałej gry będzie
równa

a zatem nie istnieje strategia wygrywająca dla pierwszego gracza. Do takiego wniosku możemy też dojść bezpośrednio. Wystarczy zauważyć, że gracz drugi może zapewnić sobie zwycięstwo przez kopiowanie ruchów gracza pierwszego na planszy, na której ostatnio nie wykonał ruchu gracz pierwszy.
Jaki związek ma twierdzenie Sprague’a–Grundy’ego z grą Grim? Jeśli startując
z łańcucha, usuniemy jeden wierzchołek, to otrzymamy dwa krótsze
łańcuchy (być może jeden pusty, czyli długości 0), z których każdy
od tej pory można traktować jako osobną grę. Chcąc wyznaczyć wartość
funkcji Sprague’a–Grundy’ego dla łańcucha długości
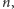 należy
obliczyć
należy
obliczyć
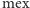 z wartości
z wartości
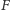 dla gier będących sumami
łańcuchów długości
dla gier będących sumami
łańcuchów długości
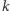 oraz
oraz
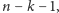 dla
dla
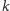 ze
zbioru
ze
zbioru
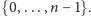 Wartość tej funkcji dla każdej takiej sumy
łańcuchów otrzymujemy z twierdzenia Sprague’a–Grundy’ego – jest to
Wartość tej funkcji dla każdej takiej sumy
łańcuchów otrzymujemy z twierdzenia Sprague’a–Grundy’ego – jest to
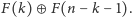 Stąd otrzymujemy definicję rekurencyjną:
Stąd otrzymujemy definicję rekurencyjną:

Powyższy przepis można bardzo efektywnie (w porównaniu
z przeszukiwaniem pełnego drzewa gry) wykorzystać do obliczenia
wartości
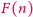 za pomocą komputera. Uproszczenie bierze się stąd, iż
zamiast rozpatrywać wszystkie możliwe konfiguracje planszy, możemy, dzięki
twierdzeniu, ograniczyć się do rozpatrywania konfiguracji będących
łańcuchem lub sumą dwóch łańcuchów. Prosta implementacja ma
pesymistyczną złożoność
za pomocą komputera. Uproszczenie bierze się stąd, iż
zamiast rozpatrywać wszystkie możliwe konfiguracje planszy, możemy, dzięki
twierdzeniu, ograniczyć się do rozpatrywania konfiguracji będących
łańcuchem lub sumą dwóch łańcuchów. Prosta implementacja ma
pesymistyczną złożoność
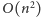 przy założeniu, że operację xor
liczymy w czasie stałym.
przy założeniu, że operację xor
liczymy w czasie stałym.
Wykorzystując tę technikę, można sprawdzić, że jedynymi liczbami
wierzchołków mniejszymi od
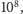 przy których strategię wygrywającą
ma gracz drugi, są dokładnie liczby ze zbioru:
przy których strategię wygrywającą
ma gracz drugi, są dokładnie liczby ze zbioru:

Pytanie, czy to jedyne liczby o tej własności, pozostaje otwarte.
Podanie jawnego wzoru na wartości funkcji Sprague’a–Grundy’ego dla różnych
dwuosobowych gier bezstronnych w ogólności uchodzi za zadanie trudne.
Obliczanie wartości tej funkcji za pomocą komputera (a nawet, przy odrobinie
wytrwałości, na kartce papieru) zazwyczaj jest dużo prostsze, a pozwala
określać, który z graczy ma strategię wygrywającą, dla konkretnych, także
nietrywialnych sytuacji. Tak otrzymane wyniki mogą prowadzić do ciekawych
hipotez dotyczących postaci funkcji
 Czytelnika Wnikliwego zachęcamy
również do wyznaczenia jawnego wzoru funkcji Sprague’a–Grundy’ego
dla gry Nim.
Czytelnika Wnikliwego zachęcamy
również do wyznaczenia jawnego wzoru funkcji Sprague’a–Grundy’ego
dla gry Nim.
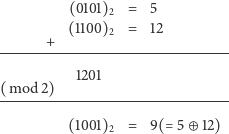
 to:
to: