Jedyny typ ruchu, jaki wolno wykonać, polega na przeskoczeniu pionkiem innego pionka, wolno to robić tylko w pionie lub w poziomie. Po wykonanym ruchu przeskoczony pionek zostaje zbity i jest usuwany z planszy. Na każdym polu w każdym momencie gry może znajdować się co najwyżej jeden pionek.

Mimo prostych zasad, niedużej planszy i niewielkiej liczby ruchów możliwych do wykonania, nie jest wcale łatwo znaleźć rozwiązanie zagadki. Można w tym celu napisać program komputerowy, który dokona symulacji możliwych ruchów i stanów w grze (nie będziemy tu jednak poruszać szczegółów).

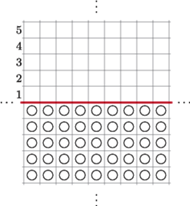
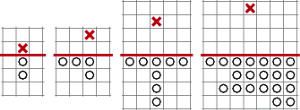
Zajmiemy się innym zadaniem. Rozważmy grę samotnik na nieskończonej planszy. Podzielmy tę planszę na dwie części poziomą linią. Poniżej tej linii, na każdym polu znajduje się po jednym pionku, powyżej zaś wszystkie pola są puste.

Zadajmy sobie teraz pytanie: czy jest możliwe wprowadzenie choćby jednego pionka do czwartego rzędu powyżej linii? Odpowiedź na to pytanie jest twierdząca. Aby się o tym przekonać, wystarczy pokazać przykładową kombinację ruchów prowadzącą do celu. Wskazówka, jak można to zrobić, znajduje się tutaj.

A czy jest możliwe wprowadzenie pionka do rzędu piątego? Skoro da się do czwartego, powinno być możliwe wprowadzenie i do piątego. Okazuje się jednak, że nie. Dalsza część tego artykułu to dowód, że taka kombinacja ruchów nie istnieje. Jeśli w tym momencie, drogi Czytelniku, zamierzasz zakończyć lekturę, zachęcam mimo wszystko do jej kontynuowania – jest to bowiem jeden z najpiękniejszych dowodów matematycznych, jakie znam. W dodatku można go tak przeprowadzić (i właśnie tak to zrobimy), aby nie było potrzeby użyć wiedzy wykraczającej poza zakres szkoły gimnazjalnej.

Załóżmy nie wprost, że wprowadzenie pionka do piątego rzędu jest możliwe. Wówczas jest możliwe osiągnięcie dowolnego pola w piątym rzędzie (wystarczy wykonać te same ruchy z odpowiednim przesunięciem). Wybierzmy zatem konkretne pole w piątym rzędzie i obierzmy je za cel.

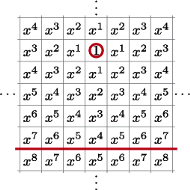
Aby badać, jak blisko celu jesteśmy, zdefiniujmy funkcję, która dla dowolnej konfiguracji pionków na planszy będzie dawać liczbę rzeczywistą: sumę wartości pól, na których stoją piony.

Jakie wartości mają pola? Ustalmy, że wartość celu wynosi 1. Wartość każdego innego pola będzie wynosić 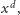 gdzie  to pewna liczba, o której powiemy za chwilę, natomiast 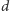 to odległość w metryce miejskiej tego pola od celu.

Ile wynosi tajemnicze 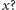 Wystarczy wiedzieć jedynie tyle, że spełnia równanie 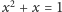 oraz należy do przedziału 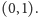 Aby dopełnić dzieła (dowodu, który można zaprezentować także młodszym Czytelnikom), wyznaczymy tę wartość dokładnie:

Zauważmy teraz, że możemy tak naprawdę zapomnieć o przeskakiwaniu pionków. Zamiast tego możemy myśleć o zamianie dwóch pionków stojących obok siebie na jeden stojący obok nich. Co w takim razie daje nasz dobór parametru 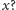 Zbadajmy, jak może się zmienić wartość konfiguracji po wykonaniu ruchu. Jest kilka przypadków, które należy rozważyć:

1.

Ruch „w górę”, czyli zamia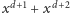na  na 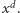 Przypomnijmy tylko, że 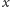 dobraliśmy tak, aby 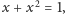 co po przemnożeniu przez 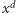 pokazuje, że suma wartości dwóch pionków, które mieliśmy, jest dokładnie równa wartości pionka, który mamy po wykonaniu ruchu.

2.

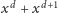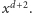Ruch „w dół”, czyli zamiana  na  Przypomnijmy tym razem, że 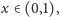 czyli 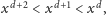 a zatem wartość konfiguracji zmalała (nowy pionek jest wart mniej niż dowolny z dwóch utraconych).

3.

Ruch „w lewo” i „w prawo”: zależnie od tego, czy taki ruch zostanie wykonany po prawej czy po lewej stronie od celu, sytuacja będzie analogiczna jak w przypadku ruchu „w górę” (gdy będziemy się do celu przybliżali) i wartość konfiguracji się nie zmieni albo będzie analogiczna jak w przypadku ruchu „w dół” (gdy od celu będziemy się oddalać) i wówczas wartość konfiguracji spadnie.

Wniosek jest taki, że po wykonaniu ruchu wartość konfiguracji może się zmniejszyć, może pozostać taka sama, ale nigdy nie może się zwiększyć.

Obliczmy teraz, ile warta jest konfiguracja początkowa. Spróbujmy wyznaczyć najpierw sumę 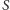 wartości pionków stojących w tej samej kolumnie co cel:

Ostatnia równość oczywiście wynika z poprzedniej dzięki skorzystaniu (po raz kolejny) z równości

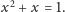
A co będzie w kolumnie obok? Suma wyniesie:

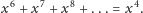Analogicznie w kolejnych kolumnach sumy wynoszą odpowiednio: 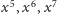 i tak dalej.

Widzimy już teraz, ile jest równa suma wartości wszystkich pionków konfiguracji początkowej:

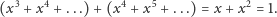Jaka jest suma wartości pionków w konfiguracji końcowej (którą podobno miało się dać osiągnąć)? Na pewno jest równa co najmniej 1 – pole będące celem jest warte dokładnie 1. Po wykonaniu skończonej liczby ruchów nadal jednak mamy nieskończenie wiele pionków do dyspozycji, a każdy z nich ma dodatnią wartość, zatem wartość konfiguracji końcowej jest większa niż 1 i mamy oczekiwaną sprzeczność. Przypomnijmy bowiem: wartość konfiguracji początkowej wynosi 1, po wykonaniu ruchu wartość konfiguracji nie rośnie, a wartość konfiguracji końcowej jest większa niż 1.

Teoretycznie trzon dowodu to zastosowanie dość standardowej techniki potencjału, jednak fakt, że wszystko składa się w całość tak łatwo i subtelnie, spowodował, że dowód uznałem za wystarczająco piękny do zaprezentowania na łamach Delty. Może Ty, szanowny Czytelniku, zechciałbyś podzielić się innym pięknym dowodem, który znasz?