O trzech grach na trzech stosach
Czy garść kamieni usypanych w trzy stosy to wystarczająco dużo, by zapewnić dwóm osobom wyzwanie intelektualne? Okazuje się, że tak! W tym artykule, używając tych właśnie akcesoriów, stworzymy trzy gry, których analiza prowadzić będzie do ciekawych i w zadziwiający sposób powiązanych ze sobą wyników.
Pierwszą z gier jest znany ludzkości od wieków Nim. Gracze wykonują ruchy
na przemian, zabierając z wybranego przez siebie stosu dowolną niezerową liczbę
kamieni. Gra kończy się przegraną gracza, który nie może wykonać ruchu,
czyli wtedy, gdy wszystkie stosy są puste. Gra Nim pojawiała się już wielokrotnie
na łamach Delty (np. w numerze 7/2010), dlatego w tym artykule ograniczymy
się jedynie do przypomnienia strategii wygrywającej w tej grze. Otóż
jeśli przez
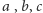 oznaczymy liczności stosów w Nimie, to to,
który z graczy wygra (o ile obaj grają optymalnie), zależy od wartości
wyrażenia
oznaczymy liczności stosów w Nimie, to to,
który z graczy wygra (o ile obaj grają optymalnie), zależy od wartości
wyrażenia

gdzie symbol
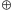 oznacza operację xor. (Aby ją wyznaczyć, zapisujemy liczby
binarnie, a następnie sumujemy metodą „szkolną”, ignorując przeniesienia.)
Dokładniej, pozycja w Nimie jest przegrywająca, gdy wartość powyższego
wyrażenia jest równa zeru – wówczas każdy ruch prowadzi do pozycji
o dodatniej wartości wyrażenia, czyli do pozycji wygrywającej. Z kolei
z każdej pozycji wygrywającej istnieje co najmniej jeden ruch do pozycji
przegrywającej. Tak samo można zresztą opisać grę Nim na większej liczbie
stosów.
oznacza operację xor. (Aby ją wyznaczyć, zapisujemy liczby
binarnie, a następnie sumujemy metodą „szkolną”, ignorując przeniesienia.)
Dokładniej, pozycja w Nimie jest przegrywająca, gdy wartość powyższego
wyrażenia jest równa zeru – wówczas każdy ruch prowadzi do pozycji
o dodatniej wartości wyrażenia, czyli do pozycji wygrywającej. Z kolei
z każdej pozycji wygrywającej istnieje co najmniej jeden ruch do pozycji
przegrywającej. Tak samo można zresztą opisać grę Nim na większej liczbie
stosów.
Rozważmy pewną drobną modyfikację w zasadach Nima. Gracze nadal wykonują ruchy na przemian, zabierając dowolną niezerową liczbę kamieni z wybranego przez siebie stosu. Dodatkowo jednak, jeden raz w ciągu gry każdy z nich może wykonać ruch specjalny. Wykonując taki ruch, gracz może zabrać kamienie z dwóch stosów (można więc ruch specjalny rozumieć jako wykonanie dwóch ruchów „zwykłych” pod rząd). Przegrywa, tak jak w zwykłym Nimie, gracz, który nie może wykonać ruchu. Nazwijmy tę zmodyfikowaną grę Nim 2.
Jak wygląda strategia dla gry Nim 2? Pierwszym kluczowym spostrzeżeniem jest to, iż nie opłaca się używać ruchu specjalnego, jeśli nie zakończy on gry. Spróbujmy to uzasadnić. Spójrzmy na sytuację gracza A, którego przeciwnik B wykonał jako pierwszy ruch specjalny. Jeżeli gra nie zakończyła się po ruchu gracza B, to możliwe są dwa przypadki. Gracz A mógł znaleźć się w pozycji wygrywającej w zwykłym Nimie – kontynuuje wtedy rozgrywkę, nie wykorzystując ruchu specjalnego, a strategia dla zwykłego Nima zapewnia mu zwycięstwo. Jeżeli zaś po ruchu specjalnym przeciwnika gracz A znajdzie się w pozycji przegrywającej, wykorzystuje natychmiast swój ruch specjalny. Po wykonaniu pierwszego ze „zwykłych” ruchów na pewno znajdzie się w pozycji wygrywającej, a następnie, za pomocą drugiego ruchu, może pozostawić przeciwnika w pozycji przegrywającej. Dalej gracz A gra zgodnie ze strategią dla zwykłego Nima.
Oczywistym wnioskiem z powyższego spostrzeżenia jest fakt, iż ruchu specjalnego należy użyć dopiero wtedy, gdy w grze pozostaną tylko dwa stosy. Ruch taki prowadzi wtedy do natychmiastowego zwycięstwa. Tym samym gracz, który doprowadzi do opróżnienia któregoś ze stosów, przegra. Jedyną sytuacją, w której opróżnienie stosu jest nieuniknione, jest ta, w której wszystkie trzy stosy mają liczność równą jeden. Stąd gracze powinni grać tak, jakby grali w zwykłego Nima na stosach o jeden kamień mniejszych! W ten sposób gracz, który nie może wykonać ruchu na „zmniejszonych” stosach, będzie zmuszony opróżnić jeden z (rzeczywistych) stosów i przegra.

Rys. 1 Zabranie dwóch kamieni z drugiego stosu w grze Nim 2 i odpowiadający temu ruch
w
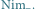
Opiszmy to nieco bardziej formalnie. Grając w Nim 2, będziemy jednocześnie
wyobrażać sobie rozgrywkę w Nim na stosach o jeden mniejszych
(nazwiemy tę grę
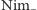 patrz również Rys. 1). Pokażemy, że jeśli
mamy strategię wygrywającą w
patrz również Rys. 1). Pokażemy, że jeśli
mamy strategię wygrywającą w
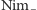 to mamy też strategię
wygrywającą w Nim 2. Aby wykonać ruch w Nim 2, patrzymy, jaki ruch
zrobilibyśmy w
to mamy też strategię
wygrywającą w Nim 2. Aby wykonać ruch w Nim 2, patrzymy, jaki ruch
zrobilibyśmy w
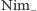 a następnie powtarzamy go w Nim 2. Z kolei gdy
nasz przeciwnik rusza się w Nim 2, to jeśli wykonał ruch specjalny lub
opróżnił jakiś stos – z dotychczas przeprowadzonego rozumowania wiemy,
że przegrał. W przeciwnym przypadku powtarzamy jego ruch w grze
a następnie powtarzamy go w Nim 2. Z kolei gdy
nasz przeciwnik rusza się w Nim 2, to jeśli wykonał ruch specjalny lub
opróżnił jakiś stos – z dotychczas przeprowadzonego rozumowania wiemy,
że przegrał. W przeciwnym przypadku powtarzamy jego ruch w grze
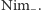
Prędzej czy później doprowadzimy przeciwnika do sytuacji w
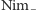 w której
nie może wykonać ruchu, bo wszystkie stosy są puste. To odpowiada sytuacji
w Nim 2, w której wszystkie stosy mają liczność jeden, zatem nasz
przeciwnik również tutaj przegrywa.
w której
nie może wykonać ruchu, bo wszystkie stosy są puste. To odpowiada sytuacji
w Nim 2, w której wszystkie stosy mają liczność jeden, zatem nasz
przeciwnik również tutaj przegrywa.
Ostatecznie wynik w grze Nim 2 będzie zależał od wartości wyrażenia

Co ciekawe, powyższe rozumowanie nie daje się uogólnić na większą liczbę stosów. Tym samym zachęcamy Czytelników do samodzielnych prób rozwiązania uogólnionej wersji gry Nim 2!
Przyjrzymy się teraz kolejnemu wariantowi gry Nim, który nazwiemy Nim 3. Tym razem modyfikacja jest taka, że po żadnym ruchu nie mogą powstać dwa stosy o równej liczbie kamieni (zakładamy, że na początku także wszystkie stosy były różne). Gra kończy się standardowo, gdy gracze nie mogą już wykonać żadnego ruchu, a zwycięża ten, który wykonał ostatni ruch. Przy czym w tej wersji sytuacją końcową jest moment, w którym stosy mają liczność 0, 1 oraz 2.
Zastanówmy się, czy Nim 3 rzeczywiście różni się od Nima z punktu
widzenia gracza, który w Nimie ma strategię wygrywającą. Przypomnijmy, że
owa strategia wygrywająca w Nimie polega na zabraniu z pewnego stosu
odpowiedniej liczby kamieni tak, aby xor liczności stosów z niezerowego stał
się zerowy. Gdybyśmy próbowali zastosować podobną strategię tutaj, to
natkniemy się na przeszkodę. Istnieją konfiguracje, w których wszystkie takie
ruchy prowadzą do wyrównania liczności pewnych stosów. Są to dość
charakterystyczne sytuacje, bo jeżeli
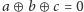 oraz, bez straty
ogólności,
oraz, bez straty
ogólności,
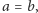 to
to
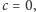 czyli jeden ze stosów musi być
pusty.
czyli jeden ze stosów musi być
pusty.
Skoro już zauważyliśmy, gdzie leży trudność w zastosowaniu standardowej taktyki, to może udałoby nam się wymyślić inną grę, w której strategia wygrywająca stałaby się bardziej jasna, a odpowiednim ruchom w niej odpowiadałyby pewne ruchy w Nim 3? Problemem, na który natknęliśmy się, stosując do gry Nim 3 strategię z Nima, było to, że gdy jeden stos stał się pusty, to ruchy, które chcielibyśmy wykonać, nagle stały się ruchami zakazanymi. Pomyślmy zatem, zamiast o Nim 3, o analogicznej grze, w której ruchem zakazanym jest także opróżnianie stosów. Zauważmy, że po dołożeniu takiego wygodnego założenia już z powodzeniem możemy zastosować standardową strategię wygrywającą dla gry Nim, gdyż ruch zerujący xora liczności wszystkich stosów nigdy nie będzie prowadził do wyrównania liczności pewnych stosów, bo jak już wcześniej zauważyliśmy, implikowałoby to, że pewien ze stosów jest pusty, a założyliśmy, że tak być nie może.
To, co nam pozostało, to sztucznie zasymulować założenie o tym, że ruch
opróżniający stos jest ruchem zakazanym. Sytuacją końcową w takiej grze
będzie układ, w którym stosy będą miały liczności
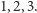 Nasuwa
się zatem pomysł, aby do każdego stosu w Nim 3 dodać po jednym
wirtualnym kamieniu, którego żaden z graczy nie może zabrać.
Zauważmy, że wtedy zarówno nie będzie możliwe opróżnienie
stosu, bo gracz nie może zabrać wirtualnego kamienia, jak i sytuacje
końcowe będą się zgadzać, bo w grze Nim 3 bez tego założenia sytuacja
końcowa miała postać
Nasuwa
się zatem pomysł, aby do każdego stosu w Nim 3 dodać po jednym
wirtualnym kamieniu, którego żaden z graczy nie może zabrać.
Zauważmy, że wtedy zarówno nie będzie możliwe opróżnienie
stosu, bo gracz nie może zabrać wirtualnego kamienia, jak i sytuacje
końcowe będą się zgadzać, bo w grze Nim 3 bez tego założenia sytuacja
końcowa miała postać
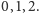 Zatem już prawie osiągnęliśmy cel –
mianowicie sprowadziliśmy Nima 3 do gry, w której będziemy mogli już
stosować standardową taktykę znaną z Nima. Pozostaje nam jedynie
formalnie udowodnić, że powyższe sprowadzenie jest rzeczywiście
poprawne.
Zatem już prawie osiągnęliśmy cel –
mianowicie sprowadziliśmy Nima 3 do gry, w której będziemy mogli już
stosować standardową taktykę znaną z Nima. Pozostaje nam jedynie
formalnie udowodnić, że powyższe sprowadzenie jest rzeczywiście
poprawne.
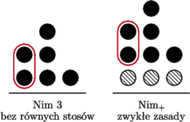
Rys. 2 Odpowiadające sobie ruchy w grach Nim 3 i
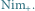
Stosujemy rozumowanie podobne jak poprzednio i, grając w Nim 3,
wyobrażamy sobie rozgrywkę w grę
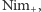 czyli w zwykłego Nima ze
stosami zwiększonymi o jeden kamień (Rys. 2). Zakładamy, że mamy strategię
wygrywającą w
czyli w zwykłego Nima ze
stosami zwiększonymi o jeden kamień (Rys. 2). Zakładamy, że mamy strategię
wygrywającą w
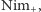 i chcemy wykazać, że mamy także strategię
wygrywającą w Nim 3. Tym razem każdy ruch przeciwnika w Nim
3 możemy powtórzyć w grze
i chcemy wykazać, że mamy także strategię
wygrywającą w Nim 3. Tym razem każdy ruch przeciwnika w Nim
3 możemy powtórzyć w grze
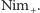 Z kolei, aby wykonać
nasz ruch w Nim 3, patrzymy na nasz ruch w
Z kolei, aby wykonać
nasz ruch w Nim 3, patrzymy na nasz ruch w
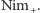 Ruch ten
prowadzi nas do sytuacji, w której xor liczności stosów jest zerowy. Gdyby
to była sytuacja, w której opróżniliśmy jeden ze stosów, to dwa
pozostałe musiałyby być równe, co nie jest możliwe, gdyż w takiej
sytuacji byłyby też równe na początku (co jest niezgodne z zasadami Nim
3). Zatem nasz ruch w
Ruch ten
prowadzi nas do sytuacji, w której xor liczności stosów jest zerowy. Gdyby
to była sytuacja, w której opróżniliśmy jeden ze stosów, to dwa
pozostałe musiałyby być równe, co nie jest możliwe, gdyż w takiej
sytuacji byłyby też równe na początku (co jest niezgodne z zasadami Nim
3). Zatem nasz ruch w
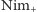 na pewno nie opróżni żadnego
stosu, czyli jest on poprawnym ruchem w Nim 3 i możemy go tam
powtórzyć.
na pewno nie opróżni żadnego
stosu, czyli jest on poprawnym ruchem w Nim 3 i możemy go tam
powtórzyć.
Zauważmy, że przez całą grę w
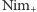 na planszy będą stosy
różnej liczności, więc w końcu doprowadzimy przeciwnika do sytuacji
na planszy będą stosy
różnej liczności, więc w końcu doprowadzimy przeciwnika do sytuacji
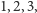 co odpowiada jego przegranej w grze Nim 3 z sytuacją
co odpowiada jego przegranej w grze Nim 3 z sytuacją
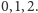
Stąd wniosek, że gracz ma w grze Nim 3 strategię wygrywającą wtedy i tylko wtedy, gdy ma on strategię wygrywającą w analogicznej konfiguracji Nima z dołożonymi wirtualnymi kamieniami – po jednym do każdego stosu, czyli wynik gry zależy od wartości wyrażenia

Kwestię uogólnienia gry Nim 3 na wiele stosów zostawiamy do rozważenia Czytelnikom.