Problem kapeluszy
Rozważmy następujący problem, zwany problemem kapeluszy (ang. hat
problem). Do pokoju wchodzi
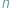 osób i każdej z nich losowo zostaje
nałożony niebieski lub czerwony kapelusz. Każdy widzi kapelusze pozostałych
osób, ale nie widzi swojego. Żadna komunikacja nie jest dozwolona,
z wyjątkiem ustalenia strategii przed rozpoczęciem gry...
osób i każdej z nich losowo zostaje
nałożony niebieski lub czerwony kapelusz. Każdy widzi kapelusze pozostałych
osób, ale nie widzi swojego. Żadna komunikacja nie jest dozwolona,
z wyjątkiem ustalenia strategii przed rozpoczęciem gry...

Po spojrzeniu na kapelusze pozostałych każdy gracz zgaduje, jaki kolor ma jego kapelusz, lub rezygnuje z próby zgadnięcia. Odpowiedzi są udzielane w taki sposób, że pozostali gracze ich nie słyszą oraz nie dowiadują się, czy odpowiadający próbował zgadnąć, czy zrezygnował i czy odpowiedź była poprawna. Uczestnicy grają całą drużyną, która wygrywa, jeżeli co najmniej jedna osoba poprawnie odgadnie kolor swojego kapelusza i nikt inny nie poda błędnej odpowiedzi. W przeciwnym przypadku drużyna przegrywa.
Problem kapeluszy z siedmioma osobami został sformułowany przez Todda
Eberta w jego rozprawie doktorskiej [1] i nazwany tam „problemem siedmiu
więźniów”. Noga Alon [2] podał ograniczenie dolne na szansę sukcesu dla
uogólnionego problemu kapeluszy z
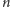 osobami i
osobami i
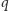 kolorami. Po
konferencji w Nowym Orleanie, dzięki której problem kapeluszy zdobył
zainteresowanie matematyków, a także mediów, w artykule w The New York
Times [3] przedstawiono problem kapeluszy z trzema osobami i jego
związek z teorią kodów Hamminga. Problem kapeluszy ma powiązania
z wieloma zagadnieniami informatycznymi i matematycznymi, na przykład
z programowaniem liniowym, programowaniem genetycznym, aproksymacją
funkcji boolowskich oraz autoredukowalnością ciągów losowych, a także
znajduje zastosowania w innych dziedzinach nauki, między innymi w biologii
i ekonomii.
kolorami. Po
konferencji w Nowym Orleanie, dzięki której problem kapeluszy zdobył
zainteresowanie matematyków, a także mediów, w artykule w The New York
Times [3] przedstawiono problem kapeluszy z trzema osobami i jego
związek z teorią kodów Hamminga. Problem kapeluszy ma powiązania
z wieloma zagadnieniami informatycznymi i matematycznymi, na przykład
z programowaniem liniowym, programowaniem genetycznym, aproksymacją
funkcji boolowskich oraz autoredukowalnością ciągów losowych, a także
znajduje zastosowania w innych dziedzinach nauki, między innymi w biologii
i ekonomii.
Problemem tym zainteresowałem się, czytając artykuł w Delcie (zob. [4]).
W tym artykule problem kapeluszy został przedstawiony w kontekście kodów
Hamminga i tzw. kodów wykrywających błędy, dzięki którym możemy, na
przykład, korzystać z płyty CD pomimo zarysowań. W kolejnym artykule
dotyczącym tego zagadnienia (zob. [5]) przedstawiono pewne modyfikacje
problemu wraz z rozwiązaniami. Autor zachęcał również czytelników do
zmierzenia się z problemem kapeluszy z trzema kolorami i
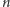 osobami.
Najprostszy przypadek, czyli zadanie z trzema osobami i trzema kolorami,
rozwiązujemy w niniejszym artykule. Jak dotąd, nie jest znane rozwiązanie
problemu dla żadnej liczby
osobami.
Najprostszy przypadek, czyli zadanie z trzema osobami i trzema kolorami,
rozwiązujemy w niniejszym artykule. Jak dotąd, nie jest znane rozwiązanie
problemu dla żadnej liczby
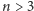 osób przy trzech kolorach
kapeluszy.
osób przy trzech kolorach
kapeluszy.
Rozpatrujemy problem kapeluszy z trzema osobami (Alicja, Bartek i Marek) i trzema kolorami (czerwony, niebieski i zielony). Podamy strategię dla tego problemu i udowodnimy, że jest ona optymalna.
Strategia
Alicja, Bartek i Marek postępują następująco.
- Alicja: jeśli Alicja widzi, że Bartek i Marek mają kapelusze różnych kolorów, to stwierdza, że ma kapelusz takiego koloru jak Marek. Jeśli zaś Bartek i Marek mają kapelusze tego samego koloru, to rezygnuje z odpowiedzi.
- Bartek: jeśli Bartek widzi, że Alicja i Marek mają kapelusze różnych kolorów, to stwierdza, że ma kapelusz takiego koloru jak Marek. Jeśli zaś Alicja i Marek mają kapelusze tego samego koloru, to rezygnuje z odpowiedzi.
- Marek: jeśli Marek widzi, że Alicja i Bartek mają kapelusze tego samego koloru, to stwierdza, że ma kapelusz takiego koloru jak oni. Jeśli zaś Alicja i Bartek mają kapelusze różnych kolorów, to rezygnuje z odpowiedzi.
Udowodnimy, że powyższa strategia jest optymalna, czyli nie istnieje żadna lepsza strategia (deterministyczna).
W naszych rozważaniach przez przypadek rozumiemy konkretny układ
kapeluszy na głowach graczy. W badanym przez nas problemie kapeluszy
z trzema osobami i trzema kolorami jest
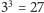 możliwych
przypadków. Przez sytuację, którą widzi dana osoba, rozumiemy układ
kapeluszy na głowach wszystkich osób poza tą jedną. W rozwiązywanym
przez nas problemie każdy widzi jedną z
możliwych
przypadków. Przez sytuację, którą widzi dana osoba, rozumiemy układ
kapeluszy na głowach wszystkich osób poza tą jedną. W rozwiązywanym
przez nas problemie każdy widzi jedną z
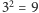 możliwych
sytuacji.
możliwych
sytuacji.
Twierdzenie 1. Powyższa strategia jest optymalna dla problemu kapeluszy z trzema osobami i trzema kolorami.
Dowód. Naszą strategię łatwo przedstawić za pomocą tabeli. Poniżej
podaliśmy kilka przykładowych wierszy tabeli dla naszej strategii. Zachęcamy
do samodzielnego wypisania dalszych wierszy, co ułatwi analizę dowodu.
W poniższej tabeli przez c, n i z oznaczamy odpowiednio kolor czerwony,
niebieski i zielony. Znak „
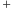 ” oznacza poprawną odpowiedź lub sukces,
znak „
” oznacza poprawną odpowiedź lub sukces,
znak „
 ” oznacza błędną odpowiedź lub porażkę, a puste pole oznacza
rezygnację z odpowiedzi. Po utworzeniu całej tabelki dowiadujemy się,
że drużyna wygrywa w
” oznacza błędną odpowiedź lub porażkę, a puste pole oznacza
rezygnację z odpowiedzi. Po utworzeniu całej tabelki dowiadujemy się,
że drużyna wygrywa w
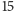 spośród
spośród
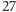 przypadków.
przypadków.

 przypadkach, czyli przegrywa w mniej niż
przypadkach, czyli przegrywa w mniej niż
 przypadkach.
przypadkach.Weźmy dowolną sytuację widzianą przez osobę
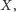 wybraną dowolnie
z trójki graczy. Udzielona odpowiedź zależy tylko od sytuacji – jest taka sama
we wszystkich przypadkach odpowiadających tej sytuacji. Wobec tego w dwóch
z trzech przypadków odpowiadających ustalonej sytuacji odpowiedź
osoby
wybraną dowolnie
z trójki graczy. Udzielona odpowiedź zależy tylko od sytuacji – jest taka sama
we wszystkich przypadkach odpowiadających tej sytuacji. Wobec tego w dwóch
z trzech przypadków odpowiadających ustalonej sytuacji odpowiedź
osoby
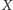 jest błędna, a w jednym jest poprawna. Czyli każda
osoba może udzielić odpowiedzi na pytanie o kolor swojego kapelusza
w co najwyżej
jest błędna, a w jednym jest poprawna. Czyli każda
osoba może udzielić odpowiedzi na pytanie o kolor swojego kapelusza
w co najwyżej
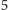 sytuacjach, bo jeśli ktoś odpowiada w co
najmniej
sytuacjach, bo jeśli ktoś odpowiada w co
najmniej
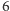 sytuacjach, to drużyna przegrywa w co najmniej
sytuacjach, to drużyna przegrywa w co najmniej
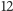 przypadkach, czyli strategia nie jest lepsza od naszej.
przypadkach, czyli strategia nie jest lepsza od naszej.
Skoro mamy trzy osoby, a każda z nich udziela odpowiedzi na pytanie
o kolor swojego kapelusza w co najwyżej pięciu sytuacjach, a każda
z tych odpowiedzi jest poprawna w dokładnie jednym przypadku, to
drużyna wygrywa w co najwyżej
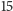 przypadkach. Jest to sprzeczne
z założeniem, że stosując rozpatrywaną strategię, drużyna wygrywa w więcej
niż
przypadkach. Jest to sprzeczne
z założeniem, że stosując rozpatrywaną strategię, drużyna wygrywa w więcej
niż
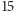 przypadkach.
przypadkach.
Czytelników serdecznie zachęcamy do prób rozwiązania póki co nierozwiązanego problemu kapeluszy z czterema osobami i trzema kolorami.