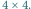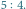Kropki – kreski
W dzisiejszym świecie ludzie stają się coraz bardziej leniwi. Chcą osiągnąć zysk w krótkim czasie, bez zbytecznej pracy. Najłatwiejszym sposobem na „zarabianie” są gry. Ale czym właściwie jest gra?
Według słownika matematycznego Edwarda Siwka jest to matematyczny model ciągu takich sytuacji, że w każdej z nich każdy uczestnik gry ma możliwość wyboru jednej spośród dostępnych dla niego decyzji (strategii), wiążącej się z określonym zyskiem lub stratą. Celem jakiejkolwiek gry zawsze będzie osiągnięcie przez nas jak największego zysku lub (w gorszej dla nas sytuacji) jak najmniejszej straty. Jednakże nie zawsze mamy wpływ na to, jak potoczy się dana rozgrywka. W niektórych przypadkach możemy liczyć jedynie na łut szczęścia (np. w Lotto czy przy rzucie monetą). Istnieją jednak gry, w których znajomość określonych strategii wygrywających może nas doprowadzić do upragnionego sukcesu. Do tego drugiego rodzaju należy gra KROPKI–KRESKI.
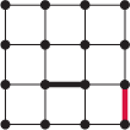
Rys. 1 Plansza
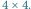
Przyjrzyjmy się zasadom gry. Toczy się ona na prostokątnej planszy zbudowanej z kropek (takiej jak na rysunku 1). Zadaniem graczy jest łączenie kolejno sąsiednich punktów liniami pionowymi lub poziomymi. W momencie, gdy cztery odcinki (niezależnie od tego, kto je narysował) utworzą kwadrat, gracz, który go zamknął, przejmuje to pole i wykonuje kolejny ruch. Wygra ten gracz, który zamknie większą liczbę kwadratów.
Większość ludzi gra w taki sposób, że linie stawiają w takich miejscach, aby nie oddać pola przeciwnikowi. Tak długo poszukują ruchów, które nie zbudują trzeciego boku kwadratu, jak tylko to jest możliwe. Tym sposobem na planszy tworzą się tzw. łańcuchy – figury, w których zamknięcie jednego kwadratu stworzy możliwość zamknięcia kolejnego pola z łańcucha przy jednym ruchu gracza. Gdy cała plansza będzie już podzielona na łańcuchy, dochodzi do blokady – jakikolwiek ruch gracza doprowadzi do zamknięcia kwadratu przez jego przeciwnika. Taki sposób gry określimy mianem gry na poziomie 0.

Rys. 2 Wynik 3:6.
Przykładową rozgrywkę prezentuje rysunek 2. Widzimy, że gracz B (czerwone kreski) utworzył blokadę złożoną z trzech łańcuchów w 12. kroku. Na poziomie 0 każdy z graczy będzie oddawał przeciwnikowi łańcuch z jak najmniejszą liczbą kwadratów (A oddaje B dwa kwadraty, B oddaje A trzy kwadraty i A oddaje B cztery kwadraty). Tym sposobem grę wygra gracz B w stosunku 6:3.
Co zatem należy zrobić, żeby wygrać? Powinniśmy przejść na wyższy poziom wtajemniczenia – poziom 1. Musimy zdać sobie sprawę, że o naszej wygranej decydować będą dwa czynniki. Po pierwsze, liczba łańcuchów podczas blokady, i po drugie, liczba kroków, po których doszło do blokady. Przy parzystej liczbie łańcuchów gracz, który otwiera pierwszy łańcuch, wygra, bo to on zamknie ostatni najdłuższy łańcuch, a każdy oddany przeciwnikowi odrobi, najczęściej z bonusem. Przy nieparzystej liczbie łańcuchów przegrywa ten, który otworzył łańcuch jako pierwszy (na rysunku w kroku 13.). Ważna jest również liczba kroków, po których doszło do blokady. W przykładzie z rysunku do blokady doszło po parzystej liczbie kroków. Zatem pierwszy łańcuch otworzy ten gracz, który zaczyna rozgrywkę; drugi gracz uczyniłby to w przypadku blokady przy nieparzystej liczbie kroków.
Załóżmy, że gracz B będzie grać na poziomie 0. Gracz A będzie dążył do tego, aby do blokady doszło po parzystej liczbie ruchów i przy parzystej liczbie łańcuchów. Jeśli mu się to uda, to albo A otworzy pierwszy z parzystej liczby łańcuchów (wygra A), albo B otworzy pierwszy z nieparzystej liczby łańcuchów (wygra A).
Jednakże gracz B również może grać na poziomie 1. Będzie on dążył do uzyskania nieparzystej sumy ruchów i łańcuchów przy blokadzie. W momencie, gdy gracz A zda sobie sprawę, że przegra, jeśli nadal będzie (tak jak jego przeciwnik) grał na poziomie 1, rezygnuje on z tej strategii na rzecz poziomu 2. W jego zamiarze jest postawienie gracza B pod tzw. przymusem. Jak może to osiągnąć? Popatrzmy na rysunek 3.
Gracz A zamiast zabrać cały łańcuch w kroku 15., podzielił go na dwie części – część zostawia sobie, a część oddaje przeciwnikowi. Gracz B został postawiony pod przymusem – cokolwiek zrobi, to otworzy graczowi A najdłuższy łańcuch. Zauważmy, że gracz A za każdym razem może zostawić ostatnie dwa kwadraty w długim łańcuchu (trzy kwadraty i więcej), tym samym powodując, że jego przeciwnik B będzie zmuszony otwierać mu kolejne łańcuchy.
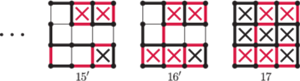
Rys. 3 Zmiana strategii w kroku 15. daje wynik
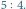
Gracz A może w ten sposób kontrolować grę. Jednakże, jeśli długość łańcucha jest równa 3, to gracz A, wykorzystując tę strategię, będzie oddawał przeciwnikowi większą część łańcucha, przy długości 4 gracze zremisują, a w sytuacji, gdy łańcuch zbudowany będzie z pięciu i więcej kwadratów, gracz A może realnie myśleć o zwycięstwie.
Tak jak każdą grę, również i tę można modyfikować. Zachęcam do tworzenia własnych plansz (np. zastępując podstawowe pole kwadratu innym wielokątem) i rozważań na temat strategii w nich występujących.