Mała Delta
Wieże Hanoi
Legenda powiada, że gdy bóg Brahma po raz pierwszy poruszył czas, umieścił na jednej z trzech diamentowych igieł, umocowanych na wspólnej podstawce, 64 złote krążki. Na podstawce spoczywał krążek najszerszy, a nad nim lśniły pozostałe o coraz mniejszych średnicach. Bóg polecił mnichom z górskiej samotni, by bez spoczynku przekładali krążki, tak aby wszystkie znalazły się na drugiej diamentowej igle, z zachowaniem tego samego ułożenia. Gdy zadanie zostanie zakończone, nastąpi koniec pierwszego świata, a na następny, wskrzeszony przez Brahmę, wypadnie czekać wiele tysięcy lat...
Nie wolno jednak przekładać krążków byle jak. Po pierwsze, w każdym ruchu można przełożyć tylko jeden krążek, a po drugie – pod żadnym pozorem nie wolno kłaść większego krążka na mniejszy. Wolno natomiast korzystać z trzeciej, pomocniczej diamentowej igły i przekładać na nią krążki, oczywiście z zachowaniem tych dwóch zasadniczych reguł.
Kiedy należy się spodziewać końca świata? Spróbujmy ustalić, ile ruchów
potrzeba, by wykonać zadanie Brahmy. Jeśli nie wiemy jeszcze, jak się do tego
zabrać, zacznijmy od prostych przypadków. Gdyby na pierwszej igle znajdował
się tylko jeden krążek, wystarczyłby jeden ruch, by przełożyć go na drugą.
Gdyby na pierwszej igle znajdowały się 2 krążki, moglibyśmy przełożyć
górny na trzecią igłę, dolny na drugą, a na koniec przełożyć mniejszy
krążek z trzeciej na drugą igłę. Razem
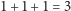 ruchy. Gdyby na
pierwszej igle były 3 krążki
ruchy. Gdyby na
pierwszej igle były 3 krążki
 Aby przełożyć na drugą igłę
największy z nich, musimy najpierw przenieść na trzecią igłę pozostałe dwa,
a to, jak wiemy, wymaga 3 ruchów. Po przełożeniu największego na
właściwe miejsce trzeba przenieść na tę samą igłę dwa mniejsze krążki
(3 ruchy). Razem
Aby przełożyć na drugą igłę
największy z nich, musimy najpierw przenieść na trzecią igłę pozostałe dwa,
a to, jak wiemy, wymaga 3 ruchów. Po przełożeniu największego na
właściwe miejsce trzeba przenieść na tę samą igłę dwa mniejsze krążki
(3 ruchy). Razem
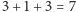 ruchów. A 4 krążki? Już się
domyślamy:
ruchów. A 4 krążki? Już się
domyślamy:
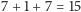 ruchów. A
ruchów. A
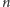 krążków? Jeśli
krążków? Jeśli
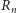 oznacza liczbę ruchów potrzebnych do prawidłowego przeniesienia
oznacza liczbę ruchów potrzebnych do prawidłowego przeniesienia
 krążków, to można przypuszczać, że dla
krążków, to można przypuszczać, że dla
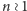 zachodzi
równość
zachodzi
równość
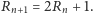 Istotnie, aby przenieść największy
z
Istotnie, aby przenieść największy
z
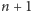 krążków, trzeba w
krążków, trzeba w
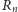 ruchach przenieść pozostałe na
trzecią igłę, jednym ruchem przełożyć największy na drugą i wreszcie
w
ruchach przenieść pozostałe na
trzecią igłę, jednym ruchem przełożyć największy na drugą i wreszcie
w
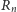 ruchach nałożyć nań mniejsze krążki.
ruchach nałożyć nań mniejsze krążki.
Ile zatem wystarczy ruchów, by przełożyć 64 krążki? Jaką liczbą jest
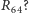 Zobaczmy:
Zobaczmy:
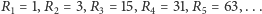 Domyślasz
się, droga Czytelniczko i drogi Czytelniku, jak
Domyślasz
się, droga Czytelniczko i drogi Czytelniku, jak
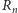 zależy od
zależy od
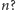 Jeśli się domyślasz i znasz zasadę indukcji matematycznej, możesz
spróbować udowodnić, że masz rację. My stwierdzimy tylko, że
Jeśli się domyślasz i znasz zasadę indukcji matematycznej, możesz
spróbować udowodnić, że masz rację. My stwierdzimy tylko, że
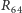 jest liczbą większą od
jest liczbą większą od
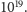 Do końca świata jeszcze
daleko.
Do końca świata jeszcze
daleko.
A co ma do tego Hanoi? Łamigłówkę z krążkami (ale tylko ośmioma) zaproponował francuski matematyk Edouard Lucas w końcu XIX wieku i nazwał ją właśnie „wieże Hanoi”. I on również ozdobił ją piękną, hinduską legendą...