Uniqueness, czyli jak oszukiwać przy rozwiązywaniu łamigłówek
Przez świat przetoczyła się niedawno mania Sudoku i, co za tym idzie, wzrosło zainteresowanie tematem łamigłówek. W tym artykule przedstawię pewne matematyczne podejście do rozwiązywania łamigłówek, które wynika nie z samej struktury zadania, a jedynie z informacji, że ma ono jednoznaczne rozwiązanie.

Rys. 1 W niektórych komórkach powyższego diagramu wstaw gwiazdy tak, aby każdy wiersz, każda kolumna oraz każdy obwiedziony grubszą linią region zawierał dokładnie dwie gwiazdy. Pola zawierające gwiazdy nie mogą się stykać (nawet rogami).

Rys. 2 Pokoloruj białe kwadraty tak, aby pola kolorowe tworzyły spójny obszar (tzn. stykały się
bokami) i pola czarne tak samo. Żaden kwadrat
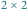 nie może się składać z pól tego
samego koloru. Na rysunku niektóre pola zostały już odpowiednio pokolorowane.
nie może się składać z pól tego
samego koloru. Na rysunku niektóre pola zostały już odpowiednio pokolorowane.
Nie będziemy się więc tutaj zajmować łamigłówkami, w których są (co najmniej) dwie różne możliwości wypełnienia diagramu prowadzące do poprawnego rozwiązania. Na pewno większości Czytelników przydarzyła się irytująca sytuacja podczas gry w windowsowego Sapera, kiedy na samym końcu rozgrywki zostały do wypełnienia dwa pola, z których dokładnie jedno zawierało minę, a obie opcje jej położenia były tak samo logiczne.
Na początek wskazówka, że przy rozwiązywaniu łamigłówek warto postarać
się o taką obserwację, która znacząco upraszcza rozwiązanie danej zagadki
logicznej i innych podobnych do niej zadań. Przykładem takiej obserwacji jest
fakt, że w każdym kwadracie magicznym
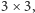 w który wpisano
cyfry od 1 do 9 włącznie, w centralnym polu musi znajdować się cyfra 5. Inny,
ciekawszy przykład to obserwacja, że jeśli mamy za zadanie wstawić do
diagramu, podzielonego na jednostkowe kwadraciki, pewną liczbę pionków tak,
aby zajęte przez nie pola nie stykały się bokami ani rogami, to w dowolnym
kwadracie
w który wpisano
cyfry od 1 do 9 włącznie, w centralnym polu musi znajdować się cyfra 5. Inny,
ciekawszy przykład to obserwacja, że jeśli mamy za zadanie wstawić do
diagramu, podzielonego na jednostkowe kwadraciki, pewną liczbę pionków tak,
aby zajęte przez nie pola nie stykały się bokami ani rogami, to w dowolnym
kwadracie
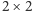 może znajdować się co najwyżej jeden pionek.
Oczywiście, obserwacje z prostszych typów zadań przenoszą się często na te
bardziej skomplikowane. Przykładem może być łamigłówka nosząca nazwę
Star Battle (Rys. 1).
może znajdować się co najwyżej jeden pionek.
Oczywiście, obserwacje z prostszych typów zadań przenoszą się często na te
bardziej skomplikowane. Przykładem może być łamigłówka nosząca nazwę
Star Battle (Rys. 1).
Sprytne spostrzeżenie całkowicie zmienia obraz problemu – o ile przed zauważeniem pewnej prawidłowości łamigłówka może wydawać się mało ciekawym zadaniem polegającym na sprawdzaniu ogromnej liczby przypadków, o tyle kluczowa obserwacja może spowodować, że bardzo szybko uzupełnimy całą planszę. Jeden z najbardziej pouczających przykładów pod tym względem to Yin Yang (Rys. 2)
Obserwacje są najciekawszą, dedukcyjną częścią łamigłówki. Odkrycie dużej liczby trików znacząco przyspiesza i upraszcza rozwiązanie problemu, a także powoduje, że zadanie daje większą satysfakcję. Co można jednak zrobić, gdy stanęliśmy w miejscu i strzał (rozpatrzenie mniej lub bardziej losowo wybranego przypadku) wydaje się już jedyną możliwą metodą posunięcia prac naprzód?
Czasami odpowiedź daje metoda uniqueness. Musimy jednak przyjąć, że autor zadania zadbał o to, żeby miało ono jednoznaczne rozwiązanie. Przy tym założeniu będziemy badać kolejne łamigłówki.

Rys. 3

Rys. 4
Korzyści z takiego założenia (o ile jesteśmy pewni, że autor sprawdził starannie, że jest spełnione) mogą być znaczne. Powiedzmy, że umiemy wywnioskować, że z poprawności pewnego rozwiązania A będzie wynikać poprawność innego rozwiązania B. Wtedy zarówno A, jak i B byłyby poprawnymi rozwiązaniami naszej łamigłówki. Jeśli rozwiązanie jest jednoznaczne, uzyskujemy sprzeczność i wnioskujemy, że rozwiązanie A nie może być poprawne. Zilustrujemy to podejście na kilku przykładach.
Na początek będziemy rozpatrywać diagram Sudoku przedstawiony na rysunku 3.
Po wpisaniu pewnej liczby cyfr dochodzimy do układu z rysunku 4. W jego opisie przyjąłem konwencję, że jeśli pole zawiera co najmniej dwie cyfry, oznacza to, że są one wszystkimi wartościami tego pola, których jeszcze nie udało nam się wyeliminować.

Rys. 5
Popatrzmy na prostokąt o wierzchołkach
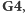
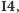
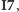
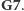 W każde z tych czterech pól można wpisać zarówno
liczbę 4, jak i 5, i to w sposób symetryczny, więc możemy zastosować
metodę uniqueness. Jeśli w
W każde z tych czterech pól można wpisać zarówno
liczbę 4, jak i 5, i to w sposób symetryczny, więc możemy zastosować
metodę uniqueness. Jeśli w
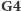 byłoby 4, to
byłoby 4, to
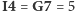 oraz
oraz
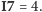 Zauważmy, że jeśli istnieje poprawne rozwiązanie,
w którym
Zauważmy, że jeśli istnieje poprawne rozwiązanie,
w którym
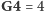 (nazwijmy je rozwiązaniem A), to istnieje także
przynajmniej jedno rozwiązanie, w którym
(nazwijmy je rozwiązaniem A), to istnieje także
przynajmniej jedno rozwiązanie, w którym
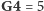 (a zatem również
(a zatem również
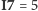 oraz
oraz
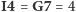 ) – rozwiązanie B. Po prostu wystarczy
zamienić w rozwiązaniu A wartości czterech wymienionych pól – po tej
zamianie wszystkie zasady Sudoku są nadal spełnione (skorzystaliśmy tu
z założenia o poprawności rozwiązania A). I vice versa: jeśli
) – rozwiązanie B. Po prostu wystarczy
zamienić w rozwiązaniu A wartości czterech wymienionych pól – po tej
zamianie wszystkie zasady Sudoku są nadal spełnione (skorzystaliśmy tu
z założenia o poprawności rozwiązania A). I vice versa: jeśli
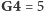 i umiemy przy tym założeniu wyprodukować pewne
rozwiązanie, to po analogicznej zamianie dostaniemy inne poprawne wypełnienie
diagramu. Zatem zostaje jedynie możliwość
i umiemy przy tym założeniu wyprodukować pewne
rozwiązanie, to po analogicznej zamianie dostaniemy inne poprawne wypełnienie
diagramu. Zatem zostaje jedynie możliwość
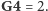 Stąd np.
Stąd np.
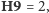 i tak dalej – dalszy ciąg rozumowania nie wymaga już użycia
metody uniqueness.
i tak dalej – dalszy ciąg rozumowania nie wymaga już użycia
metody uniqueness.
Inny ciekawy przykład to diagram Diamonds, pokazany na rysunku 5. Należy rozmieścić podaną liczbę diamentów w pustych polach planszy tak, aby każda cyfra dawała informację, ile dokładnie pól sąsiadujących bokiem lub rogiem z tą cyfrą zawiera diament.
Niektóre pola oznaczyłem na rysunku literami od A do H. Przyjrzyjmy się komórkom, w których znajdują się litery A, B i C. Jest to dobre miejsce do zastosowania świeżo poznanej umiejętności. Pola te sąsiadują z cyfrą 1 i żadna inna cyfra nie sąsiaduje z tymi polami. Zatem jeśli w pewnym z nich (np. w A) jest diament, to równie dobrze moglibyśmy umieścić diament w B czy w C, zamiast w A. W słowach „równie dobrze” przemyciłem (już pewnie w tym momencie intuicyjny) fakt, że z jednego poprawnego rozwiązania wyniknie poprawność innych konfiguracji, co stoi w sprzeczności z jednoznacznością rozwiązania. Zatem w żadnym z pól A, B, C nie ma diamentu. Czytelnik Wnikliwy zauważy, że podobne rozważania można przeprowadzić dla trójki D, E, F oraz dla pary G, H, tylko że w tych przypadkach w każdym z oznaczonych pól będzie znajdował się diament.

Rys. 6
Ten diagram dostarcza nam jeszcze jednego przykładu użycia strategii uniqueness. Po prawidłowym rozmieszczeniu większości diamentów fragment planszy wygląda jak na rysunku 6.
Jak dokończyć rozwiązanie, nie zliczając już ustawionych diamentów? Pozostawiam to ćwiczenie Czytelnikom.
Ostatni przykład dotyczy łamigłówki nazywanej po polsku Pokropkiem. Na angielskich stronach internetowych najczęściej można ją znaleźć pod nazwą Slitherlink lub Fences.
Można powiedzieć, że możliwość A „zabiera nam więcej miejsca”. Ściślej, jeśli rozwiązanie z wykorzystaniem ustawienia A jest poprawne, to rozwiązanie z wykorzystaniem ustawienia B tym bardziej (oczywiście należy dokładnie sprawdzić, że wszystkie reguły Pokropka będą spełnione). Dalej, z metody uniqueness uzyskujemy nie tylko wniosek, że przejście B jest poprawne. Ważne jest także to, że A nie jest poprawne. To oznacza, że konieczne jest poprowadzenie odcinków oznaczonych literami X i Y, gdyż w przeciwnym przypadku z poprawności rozwiązania z wykorzystaniem ustawienia B moglibyśmy wyprowadzić poprawność rozwiązania z wykorzystaniem A.
Ostatnie zadanie jest modyfikacją fragmentu diagramu nr 10 z pierwszej części finału XII Mistrzostw Polski w Łamaniu Głowy zorganizowanych w 2008 roku przez fundację Sfinks. O ile w powyższym przypadku znalezienie rozwiązania bez użycia strategii uniqueness jest nietrudne, to we właściwym zadaniu finałowym zauważenie powyższej sytuacji i wykorzystanie tej metody ogromnie upraszczało znalezienie właściwej ścieżki i istotnie zmniejszało użycie metody prób i błędów.
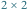 nie może się składać z pól tego
samego koloru. Na rysunku niektóre pola zostały już odpowiednio pokolorowane.
nie może się składać z pól tego
samego koloru. Na rysunku niektóre pola zostały już odpowiednio pokolorowane.



