Dwa takie przykłady opisano w Deltoidzie 7/2010. Oto dwa kolejne.

Gra 1. Każde z następujących dziewięciu słów napisano na osobnym kartoniku:

Dwaj gracze na przemian biorą sobie po jednym kartoniku. Wygrywa gracz, który jako pierwszy skompletuje trzy wyrazy zawierające tę samą literę.

Czy któryś z graczy może zawsze wygrać? Jeśli tak, to który i jak?

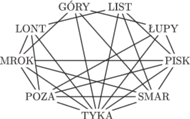
Rys. 1

Rys. 2 Kolorem napisano nieistotne litery.

Połączmy liniami słowa zawierające te same litery, czyli narysujmy graf, którego wierzchołkami są słowa, a krawędź oznacza wspólną literę (Rys. 1). Jak widać  nic nie widać, trzeba więc jakoś ten graf uprościć.

Możemy nie rozważać liter nieistotnych – występujących tylko w jednym lub dwóch słowach (np. G, M), bo nie da się skompletować trzech wyrazów z taką literą. Każda z pozostałych liter występuje w dokładnie trzech słowach. Ponadto dowolne dwa wyrazy mają najwyżej jedną wspólną istotną literę.

W grafie na rysunku 2 każde trzy słowa o wspólnej literze leżą na jednej prostej i na odwrót, każde trzy słowa „współliniowe” mają wspólną literę. Narysowano tylko krawędzie od pierwszego z takich słów do drugiego i od drugiego do trzeciego, a krawędź między pierwszym a trzecim (np. POZA-MROK) jest „w domyśle”.

Celem gry jest skompletowanie trzech słów o wspólnej literze, czyli słów z jednego wiersza, jednej kolumny lub jednej przekątnej na rysunku 2. Czyż nie wygląda to znajomo? Ta gra to nic innego niż zakamuflowane „kółko i krzyżyk”! Kto kiedykolwiek grał w  „kółko i krzyżyk”, wie już, jak grać, żeby nie przegrać. Gra zazwyczaj kończy się remisem i, niestety, traci na atrakcyjności  chyba że gramy z niewtajemniczonym przeciwnikiem!

Gra 2 (jednoosobowa). Danych jest dziesięć kartoników z następującymi słowami:

Celem gracza jest ułożenie ich „w kółko” tak, by każde dwa sąsiadujące słowa miały wspólną literę. Powyższa kolejność byłaby rozwiązaniem, gdyby słowa SET i BAL miały wspólną literę.

Czy rozwiązanie istnieje? Jeśli tak, to jak je znaleźć?

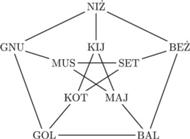
Rys. 3

Znów narysujmy graf, łącząc krawędziami słowa o wspólnych literach. Można osiągnąć efekt podobnie nieczytelny, jak na rysunku 1, ale można też rozmieścić wierzchołki tak, jak na rysunku 3. Uzyskujemy tzw. graf Petersena. Celem gry jest znalezienie cyklu przechodzącego przez każdy wierzchołek grafu dokładnie raz, czyli tzw. cyklu Hamiltona. Niestety, tego w grafie Petersena zrobić się nie da  ale jak to udowodnić bez sprawdzania wszystkich możliwości?

Gdyby cykl Hamiltona istniał, miałby 10 krawędzi (bo tyle jest słów). Można by pokolorować je na przemian w dwóch kolorach i w każdym wierzchołku trzecią z wychodzących z niego krawędzi pomalować trzecim kolorem. Oznaczałoby to, że graf Petersena jest 3-barwny krawędziowo, tzn. można tak pomalować jego krawędzie trzema kolorami, by krawędzie o wspólnych wierzchołkach miały różne kolory.

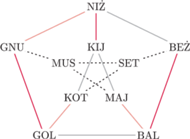
Rys. 4

Przypuśćmy więc, że graf Petersena jest 3-barwny krawędziowo. Wtedy pewne dwie niesąsiednie spośród pięciu krawędzi obwodu są jednego koloru, powiedzmy GOL-GNU i BAL-BEŻ (Rys. 4). Krawędź GOL-BAL jest wówczas drugiego koloru, zatem obie krawędzie GOL-KOT i BAL-MAJ są w kolorze trzecim. Jednocześnie jedna z krawędzi NIŻ-GNU, NIŻ-BEŻ jest drugiego koloru, a jedna trzeciego, więc krawędź NIŻ-KIJ jest w kolorze pierwszym. Wynika z tego, że obie krawędzie KIJ-KOT i KIJ-MAJ są tego samego koloru (drugiego), sprzecznie z założeniem.

Stąd graf Petersena nie jest 3-barwny krawędziowo, a więc nie ma w nim cyklu Hamiltona, czyli gra 2 nie ma rozwiązania.

Zadanie domowe
Czy gra 2 ma rozwiązanie, jeśli słowa KOT i MUS zastąpić słowami TOM i SUK?