O kapeluszach i pewnym pewniku
O ciekawych problemach związanych z kapeluszami pisaliśmy już w Delcie nie raz, ale że dobrego nigdy za wiele, napiszemy też i w tym numerze, tyle że inaczej.
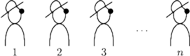
Problem. W rzędzie stoi
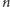 osób i każdej z nich nałożony został
na głowę biały lub czarny kapelusz. Każda widzi kapelusze tych osób, które
stoją przed nim, zatem pierwsza osoba widzi kapelusze wszystkich pozostałych,
natomiast ostatnia osoba nie widzi żadnego (rysunek). Oczywiście, nikt
nie widzi swojego kapelusza i w tym cała zabawa, gdyż zadaniem każdej
z osób jest odgadnięcie, jakiego koloru kapelusz ma na głowie. Uczestnicy
zabawy odgadują po kolei, począwszy od pierwszej osoby w rzędzie, i każdy
słyszy odpowiedzi poprzedników. Uznajemy, że się udało, jeśli błędnej
odpowiedzi udzieliła nie więcej niż jedna osoba. A jak to z zabawami
bywa, warto, by były udane. Z tego też powodu uczestnicy, przed
nałożeniem kapeluszy na ich głowy, mogą się naradzić i ustalić wspólną
strategię postępowania.
osób i każdej z nich nałożony został
na głowę biały lub czarny kapelusz. Każda widzi kapelusze tych osób, które
stoją przed nim, zatem pierwsza osoba widzi kapelusze wszystkich pozostałych,
natomiast ostatnia osoba nie widzi żadnego (rysunek). Oczywiście, nikt
nie widzi swojego kapelusza i w tym cała zabawa, gdyż zadaniem każdej
z osób jest odgadnięcie, jakiego koloru kapelusz ma na głowie. Uczestnicy
zabawy odgadują po kolei, począwszy od pierwszej osoby w rzędzie, i każdy
słyszy odpowiedzi poprzedników. Uznajemy, że się udało, jeśli błędnej
odpowiedzi udzieliła nie więcej niż jedna osoba. A jak to z zabawami
bywa, warto, by były udane. Z tego też powodu uczestnicy, przed
nałożeniem kapeluszy na ich głowy, mogą się naradzić i ustalić wspólną
strategię postępowania.
W tym momencie zachęcamy Czytelników do przerwania lektury
i zastanowienia się, dla jakich
 istnieje strategia gwarantująca
wygraną.
istnieje strategia gwarantująca
wygraną.
Spróbujmy w następujący sposób: pierwsza osoba, nieważne, jak będzie
się starać, ma 50% szans na odgadnięcie koloru swojego kapelusza.
W pesymistycznym przypadku musimy więc założyć, że udzieli błędnej
odpowiedzi i tym samym wykorzysta cały dostępny limit pomyłek. Pogodzeni
z tym faktem, spróbujemy w jej odpowiedzi przemycić bit informacji dla
pozostałych uczestników. Oznaczmy przez
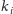 kolor kapelusza
kolor kapelusza
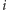 -tej
osoby (
-tej
osoby (
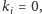 jeśli jest to biały kapelusz, i
jeśli jest to biały kapelusz, i
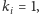 jeśli kapelusz
jest czarny), a przez
jeśli kapelusz
jest czarny), a przez
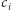 liczbę czarnych kapeluszy, które
liczbę czarnych kapeluszy, które
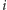 -ta osoba
widzi przed sobą.
-ta osoba
widzi przed sobą.
Zrobimy teraz tak: pierwsza osoba mówi „biały”, jeśli
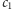 jest parzyste,
a w przeciwnym przypadku mówi „czarny”. Co nam z tego przyjdzie? Ano
tyle, że ta informacja wystarczy, by druga osoba bezbłędnie odgadła kolor
swojego kapelusza. W istocie, ponieważ
jest parzyste,
a w przeciwnym przypadku mówi „czarny”. Co nam z tego przyjdzie? Ano
tyle, że ta informacja wystarczy, by druga osoba bezbłędnie odgadła kolor
swojego kapelusza. W istocie, ponieważ
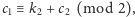 zatem
usłyszawszy przed chwilą wartość
zatem
usłyszawszy przed chwilą wartość
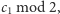 bez trudu wyznaczy ona
bez trudu wyznaczy ona
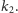 Co więcej, każda kolejna osoba może postąpić podobnie,
korzystając z faktu, że
Co więcej, każda kolejna osoba może postąpić podobnie,
korzystając z faktu, że

oraz z tego, że zna wartości
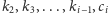 oraz
oraz
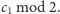 Potrafimy
więc znaleźć strategię dla dowolnie dużego
Potrafimy
więc znaleźć strategię dla dowolnie dużego
 I tu nasuwa się pytanie:
a co, jeśli
I tu nasuwa się pytanie:
a co, jeśli
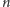 byłoby nieskończone? Innymi słowy, mamy nieskończony
rząd osób, w którym
byłoby nieskończone? Innymi słowy, mamy nieskończony
rząd osób, w którym
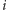 -ta osoba widzi kapelusze wszystkich osób
o większych numerach (jest ich, oczywiście, nieskończenie wiele). Czy i tym
razem będzie istniała strategia? Podkreślmy, że nie osłabiamy żadnej z reguł
zabawy, zatem nadal dopuszczamy tylko jedną pomyłkę. Zauważmy też, że
nasza strategia dla skończonego
-ta osoba widzi kapelusze wszystkich osób
o większych numerach (jest ich, oczywiście, nieskończenie wiele). Czy i tym
razem będzie istniała strategia? Podkreślmy, że nie osłabiamy żadnej z reguł
zabawy, zatem nadal dopuszczamy tylko jedną pomyłkę. Zauważmy też, że
nasza strategia dla skończonego
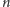 nie będzie tu działać, gdyż
nie będzie tu działać, gdyż
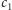 może nie być liczbą naturalną.
może nie być liczbą naturalną.
Odpowiedź jest nieco zaskakująca: strategia istnieje. Po raz drugi zachęcamy Czytelników, aby przez (być może dłuższą) chwilę zmierzyli się z tym zadaniem samodzielnie.
Nieskończony ciąg
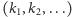 kolorów kapeluszy oznaczać będziemy
przez
kolorów kapeluszy oznaczać będziemy
przez
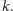 Powiemy, że dwa nieskończone ciągi
Powiemy, że dwa nieskończone ciągi
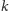 i
i
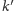 są
w relacji
są
w relacji
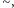 jeśli różnią się na skończenie wielu pozycjach.
Piszemy więc
jeśli różnią się na skończenie wielu pozycjach.
Piszemy więc
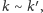 jeśli zbiór
jeśli zbiór
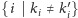 jest skończony.
Łatwo przekonać się, że tak zdefiniowana relacja
jest skończony.
Łatwo przekonać się, że tak zdefiniowana relacja
 jest relacją
równoważności. I teraz z pomocą przychodzi nam wspomniany w tytule
pewien pewnik, a konkretnie pewnik wyboru – nieocenione źródło
matematycznych paradoksów. Dzięki niemu możemy dla każdej klasy
abstrakcji relacji
jest relacją
równoważności. I teraz z pomocą przychodzi nam wspomniany w tytule
pewien pewnik, a konkretnie pewnik wyboru – nieocenione źródło
matematycznych paradoksów. Dzięki niemu możemy dla każdej klasy
abstrakcji relacji
 wybrać jej reprezentanta i poinformować
wszystkich o tym, który został wybrany. Innymi słowy, istnieje taka funkcja
wybrać jej reprezentanta i poinformować
wszystkich o tym, który został wybrany. Innymi słowy, istnieje taka funkcja
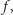 określona na zbiorze wszystkich ciągów kolorowań kapeluszy,
która dla dowolnego
określona na zbiorze wszystkich ciągów kolorowań kapeluszy,
która dla dowolnego
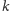 spełnia
spełnia
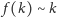 oraz dla dowolnych
oraz dla dowolnych
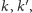 jeśli
jeśli
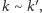 to
to
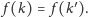 Zauważmy teraz, że
jeśli uczestnicy porozumieją się co do wyboru funkcji
Zauważmy teraz, że
jeśli uczestnicy porozumieją się co do wyboru funkcji
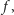 to każdy
z nich będzie mógł obliczyć ten sam ciąg
to każdy
z nich będzie mógł obliczyć ten sam ciąg
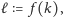 gdyż nie zna on
tylko skończonej liczby wyrazów ciągu
gdyż nie zna on
tylko skończonej liczby wyrazów ciągu
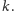 Zauważmy też, że jeśli
teraz
Zauważmy też, że jeśli
teraz
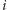 -ty zawodnik odpowie
-ty zawodnik odpowie
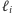 (nawet nie czekając na odpowiedzi
poprzedników), to ponieważ
(nawet nie czekając na odpowiedzi
poprzedników), to ponieważ
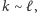 więc będziemy mieli tylko
skończoną liczbę pomyłek.
więc będziemy mieli tylko
skończoną liczbę pomyłek.
W tym momencie spróbujemy wyeliminować te pomyłki metodą analogiczną
jak w przypadku skończonym. Oznaczmy przez
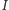 zbiór numerów
osób (poza pierwszą), których kolory kapeluszy
zbiór numerów
osób (poza pierwszą), których kolory kapeluszy
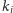 nie zgadzają się
z kolorami w ciągu
nie zgadzają się
z kolorami w ciągu
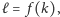 czyli
czyli
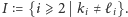 Skoro
Skoro
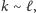 to zbiór
to zbiór
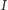 jest skończony. Niech
jest skończony. Niech
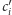 będzie
liczbą osób ze zbioru
będzie
liczbą osób ze zbioru
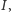 które widzi osoba
które widzi osoba
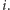 Niech też
Niech też
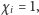 jeśli
jeśli
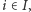 oraz
oraz
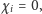 gdy
gdy
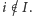 Każda
z osób (poza pierwszą) musi zdecydować, czy nie należy do zbioru
Każda
z osób (poza pierwszą) musi zdecydować, czy nie należy do zbioru
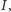 i wtedy odpowiada zgodnie z
i wtedy odpowiada zgodnie z
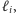 czy też należy (i wtedy musi
odpowiedzieć przeciwnie). Pierwsza osoba podaje
czy też należy (i wtedy musi
odpowiedzieć przeciwnie). Pierwsza osoba podaje
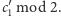 Druga
osoba wie, że
Druga
osoba wie, że
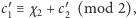 jest więc w stanie wyznaczyć
jest więc w stanie wyznaczyć
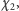 stwierdzić, czy należy do
stwierdzić, czy należy do
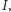 i odpowiedzieć poprawnie.
Analogicznie
i odpowiedzieć poprawnie.
Analogicznie
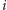 -ta osoba oblicza
-ta osoba oblicza
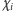 z zależności
z zależności

oraz z faktu, że
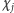 dla
dla
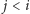 jest równe 1 wtedy i tylko
wtedy, gdy
jest równe 1 wtedy i tylko
wtedy, gdy
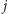 -ta osoba udzieliła odpowiedzi niezgodnej z wartością
-ta osoba udzieliła odpowiedzi niezgodnej z wartością
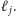 I to by było na tyle, gdyby nie to, że pokazując istnienie strategii dla
I to by było na tyle, gdyby nie to, że pokazując istnienie strategii dla
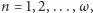 otwieramy drogę kolejnym pytaniom: a co, jeśli
otwieramy drogę kolejnym pytaniom: a co, jeśli
 jest liczbą porządkową większą niż
jest liczbą porządkową większą niż
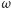 ? Zastanówmy się więc
nad istnieniem strategii w przypadku
? Zastanówmy się więc
nad istnieniem strategii w przypadku
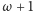 (czyli za nieskończonym
rzędem osób stoi jeszcze jeden uczestnik o numerze
(czyli za nieskończonym
rzędem osób stoi jeszcze jeden uczestnik o numerze
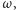 który
odpowiada na samym końcu). Czytelnik znów zdecyduje, na jak długo
przerwać w tym miejscu lekturę.
który
odpowiada na samym końcu). Czytelnik znów zdecyduje, na jak długo
przerwać w tym miejscu lekturę.
Wydawać by się mogło, że nie da się uniknąć co najmniej dwóch pomyłek,
gdyż osoba
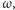 nie widząc nikogo innego, musi wprost otrzymać
kolor swojego kapelusza, co wymagałoby przekazania dodatkowego bitu
informacji. Jednak nie należy zapominać o tym, że usłyszała ona
odpowiedzi wszystkich pozostałych uczestników, zatem zna kolory kapeluszy
nie widząc nikogo innego, musi wprost otrzymać
kolor swojego kapelusza, co wymagałoby przekazania dodatkowego bitu
informacji. Jednak nie należy zapominać o tym, że usłyszała ona
odpowiedzi wszystkich pozostałych uczestników, zatem zna kolory kapeluszy
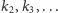 (wszak ci uczestnicy odpowiadali poprawnie). Jest zatem
w stanie obliczyć ciąg
(wszak ci uczestnicy odpowiadali poprawnie). Jest zatem
w stanie obliczyć ciąg
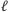 i tym samym zbiór
i tym samym zbiór
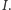 W tym
momencie łatwo już jest zmodyfikować strategię: pierwsza osoba zamiast
W tym
momencie łatwo już jest zmodyfikować strategię: pierwsza osoba zamiast
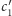 podaje
podaje
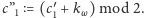 Pozostałe osoby o numerach
naturalnych, widząc
Pozostałe osoby o numerach
naturalnych, widząc
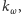 są w stanie odzyskać
są w stanie odzyskać
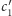 i grać
jak poprzednio. Natomiast uczestnik
i grać
jak poprzednio. Natomiast uczestnik
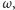 znając
znając
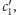 bez trudu
oblicza
bez trudu
oblicza
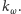
Łatwo wskazać, jak zmodyfikować powyższą strategię, by działała
w przypadku
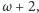
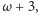 a nawet
a nawet
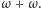 A jaką
strategię zastosować dla
A jaką
strategię zastosować dla
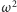 ? A
? A
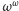 ? A może dla każdej
liczby porządkowej można wskazać analogiczną strategię? Wreszcie,
co w przypadku, gdy mamy więcej kolorów kapeluszy?
? A może dla każdej
liczby porządkowej można wskazać analogiczną strategię? Wreszcie,
co w przypadku, gdy mamy więcej kolorów kapeluszy?