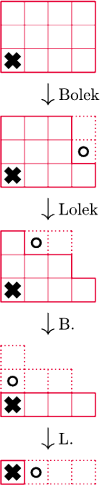
Rys. 1 Przykładowy przebieg gry.

Rys. 2

Rys. 3

Jak łatwo się domyślić, gracz, który zje truciznę, przegrywa. Grę rozpoczyna zawsze Bolek, a potem chłopcy ruszają się na zmianę (Rys. 1). Zastanowimy się nad pytaniem, który z nich ma strategię wygrywającą.

Żeby odpowiedzieć na to pytanie, spróbujmy najpierw rozwiązać najprostsze przypadki. Dla czekolady o wymiarach 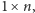 gdzie 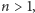 czyli będącej poziomym paskiem, rozwiązanie jest łatwe. Bolek wybiera drugi kawałek od lewej i zjada go razem z całą resztą leżącą na prawo od niego (Rys. 2). W ten sposób zostawia Lolkowi jedynie kawałek z trucizną, którą ten niechybnie zje, tym samym przegrywając.

Wytrawni Czytelnicy znają z pewnością trik polegający na wykorzystaniu symetrii gry. To pozwoli nam rozwiązać kolejny przypadek. Jeżeli czekolada ma wymiary 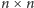 dla 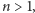 to Bolek również może zapewnić sobie wygraną. W pierwszym ruchu zjada kwadrat o boku 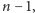 zostawiając Lolkowi poziomy pasek o wysokości 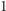 i szerokości 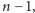 pionowy pasek o wysokości 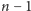 i szerokości 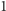 oraz truciznę (Rys. 3). Następnie Bolek naśladuje ruchy Lolka: wykonuje to samo, tylko w innym pasku. Przykładowo, gdy Lolek zje trzy kawałki z poziomego paska, Bolek odpowie mu zjedzeniem trzech kawałków z pionowego paska. Tym sposobem nigdy nie zje trucizny i w pewnym momencie doprowadzi Lolka do sytuacji sam na sam z jednym, zatrutym kawałkiem czekolady.

Dalej jest coraz trudniej, ale rozważymy jeszcze jeden przypadek. Dla czekolady o wymiarach 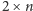 Bolek także ma strategię wygrywającą. Tym razem pozostawia on Lolkowi po swoim ruchu część czekolady w kształcie schodka, to znaczy w dolnym rzędzie jest  kawałków, a w górnym 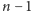 (Rys. 4). Krótka analiza przypadków pozwoli nam stwierdzić, że niezależnie od ruchu Lolka w następnym ruchu Bolek może znów doprowadzić do takiej właśnie sytuacji. Grając zgodnie z tą strategią, nie zje nigdy trucizny, więc po pewnej liczbie ruchów musi zjeść ją Lolek.

W tym miejscu zaczynają się schody. Naprawdę nie jest łatwo znaleźć jeszcze jakąś szczególną sytuację, w której można opisać strategię – polecam samodzielne próby rozpatrzenia wybranych przypadków.

Z pomocą przychodzi nam nieintuicyjna metoda zwana podkradaniem strategii. Udowodnimy, że Bolek ma strategię wygrywającą zawsze, niezależnie od wymiarów czekolady, jednak takiej strategii nie wskażemy.

Przypuśćmy nie wprost, że to Lolek ma strategię wygrywającą; doprowadzimy do sprzeczności. Rozważmy następującą strategię Bolka. W pierwszym ruchu zjada on tylko jeden mały kwadracik z prawego górnego rogu i od tej chwili „kradnie” strategię Lolka. To oznacza, że w swoim ruchu Bolek patrzy, jak w tej sytuacji ruszyłby się Lolek (możemy przyjąć, że strategia Lolka jest znana), i rusza się dokładnie w ten sposób. Pamiętajmy, że strategia Lolka jest wygrywająca, więc zgodnie z naszym założeniem, mimo wszystkich swoich wysiłków, Bolek przegra.

Do celów dalszych rozważań oznaczmy kształty czekolady po 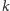-tym ruchu Bolka i Lolka odpowiednio przez 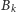 i 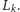 Czyli kolejne konfiguracje w grze to:

gdzie 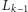 składa się z jednego, zatrutego kawałka czekolady, a 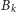 jest puste (skoro Bolek przegra, to zje ostatni kawałek, co zakończy grę).

Udowodnimy teraz, że wbrew wcześniejszym założeniom jednak wygra Bolek. Przypomnijmy, że 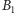 to prostokąt bez jednego kawałka w prawym górnym rogu. Przyjrzyjmy się pierwszemu ruchowi Lolka, z 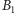 do 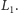 Dokonajmy kluczowej obserwacji – kształt 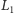 to z pewnością cała czekolada bez pewnej prostokątnej części w prawym górnym rogu. Tylko do takich kształtów jest w stanie doprowadzić Lolek z 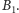 Jednak taką sytuację Bolek mógł osiągnąć już w pierwszym swoim ruchu. Spójrzmy więc, jak wówczas potoczyłaby się rozgrywka.

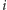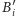Kształty czekolady w tej rozgrywce po -tym ruchu Bolka i Lolka oznaczmy odpowiednio  oraz 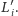 Mamy 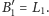 Zauważmy jednak, że w obu rozgrywkach zarówno Lolek, jak i Bolek, stosują tę samą strategię – strategię wygrywającą Lolka, którą to Bolek właśnie podkrada. Zatem ta rozgrywka potoczyłaby się dokładnie tak samo, jak rozważana przed chwilą; jedyna różnica polega na tym, że wszystko odbywa się tu o ruch wcześniej. Skoro wszystko jest przesunięte o jeden ruch, to zauważamy, że zatruty kawałek tym razem zjada Lolek. A przecież jego strategia miała być wygrywająca  Żeby to precyzyjnie uzasadnić, napiszmy, że ciąg otrzymanych kształtów czekolady wygląda następująco:

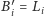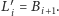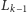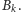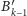gdzie  oraz  Skoro tak, to rozgrywka zakończy się dokładnie tak, jak opisywana wcześniej, czyli na ruchu z kształtu  do kształtu  W rozpatrywanej teraz rozgrywce te pozycje są oznaczone odpowiednio  oraz 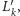 czyli ostatni ruch (zjedzenie trucizny) wykonuje Lolek – to on przegrywa. Otrzymujemy w ten sposób sprzeczność z założeniem, że istnieje strategia wygrywająca dla Lolka.

Rys. 4

Wykazaliśmy więc, że strategii wygrywającej nie może mieć Lolek. Korzystając z twierdzenia mówiącego, że dla gier takich jak czekolada dokładnie jeden z graczy ma strategię wygrywającą, dostajemy, że musi mieć ją Bolek. Twierdzenie to nie jest trudne, ale na tym marginesie jest zbyt mało miejsca, by je udowodnić. Idea dowodu polega na rozpatrywaniu drzewa gry, które jest ograniczone, i uzasadnianiu, że w tej sytuacji z dowolnego jego wierzchołka dokładnie jeden gracz ma strategię wygrywającą.

Argument podkradania strategii (ang. strategy stealing) jest użyteczny przy analizie wielu innych gier. Pozwala wykazać, na przykład, że w grach go, hex, gomoku (kółko i krzyżyk do pięciu na planszy 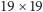) i wielu innych wygrywa pierwszy gracz. Zazwyczaj, tak jak dla czekolady, jego użycie jest niezwykle proste, a pozwala uzasadnić istnienie strategii, od których znalezienia jesteśmy bardzo dalecy.

W przypadku gry go argument podkradania strategii działa z bardzo prostej przyczyny – po prostu wstrzymywanie się od ruchu jest dozwolone. Stąd w oczywisty sposób gracz pierwszy mógłby ukraść strategię gracza drugiego, wstrzymując się przy pierwszym ruchu. Ciekawe, że chociaż wiemy, który gracz wygrywa, znalezienie strategii dla niego jest niesłychanie trudne. Najlepsze programy komputerowe grające w szachy wygrywają z szachowym mistrzem świata, dla go zaś grają jedynie na poziomie początkującego. Dotychczas największy rozmiar planszy, dla którego znaleziona została strategia wygrywająca, to 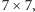 a oryginalną grę rozgrywa się na planszy 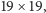 więc do pełnego sukcesu jeszcze dużo brakuje.

Dla gomoku powód działania podkradania strategii jest nieco inny, ale również nietrudny. Po prostu postawiony krzyżyk lub kółko nigdy nie przeszkadza graczowi, który go postawił. Zatem pierwszy gracz może postawić swój znak i dalej grać tak, jak gdyby wcale tego nie zrobił. Gdy w pewnym momencie strategia zmusi go do postawienia znaku w miejscu, gdzie ten już jest, to on postawi go po prostu gdzie indziej, i tak dalej.

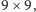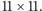Z kolei dla gry hex rozwiązanie jest dalece nietrywialne. Tę grę wymyślił John Nash i to on znalazł gracza wygrywającego. Trudność polega na wykazaniu, że w tej grze nigdy nie ma remisów – wówczas argument działa w podobny sposób jak dla gomoku. Dla hex największa plansza, dla której znana jest strategia wygrywająca, to  podczas gdy zwykle gra się na   Z pewnością jest jeszcze wiele gier, w których trik z podkradaniem strategii się przydaje – przyjemność odnajdywania ich i badania pozostawiam Czytelnikom.