Następnego dnia przed południem zostaną oni ponownie zgromadzeni w tej samej komnacie i ustawieni jeden za drugim. Król każdemu włoży na głowę czarną lub białą czapkę, przy czym nie ma żadnego ograniczenia dotyczącego liczby nakryć głowy w danym kolorze. Każdy mędrzec widzieć będzie tylko czapki wszystkich stojących przed nim i zadaniem każdego będzie określić, jaką czapkę ma na własnej głowie. W samo południe jeden z nich powinien zabrać głos, podając domniemany kolor swojej czapki. Minutę po nim powinien odezwać się kolejny, również wypowiadając słowo „czarna” lub „biała”. I tak dalej – mędrcy mają, oczywiście bez dodatkowego porozumiewania się, odzywać się pojedynczo, w jednominutowych odstępach, w dowolnej kolejności, ale każdy dokładnie raz. Złamanie którejkolwiek z tych zasad grozi natychmiastową śmiercią wszystkich mędrców. Kiedy już każdy zadeklaruje kolor swojej czapki, sprawdzian się zakończy. Wtedy król obwieści, kto odgadł poprawnie i rozkaże ściąć głowy pozostałym.

Mędrcy mają zatem całą noc na opracowanie algorytmu odzywania się i odgadywania kolorów czapek. Nie lubią ryzyka, więc szukają takiej wspólnej strategii, która daje stuprocentową gwarancję przeżycia jak największej liczbie spośród nich. Jaka to strategia?

Wskazówki, czyli o różnych strategiach

Nietrudno dostrzec strategię, pozwalającą ocalić co drugiego mędrca: wystarczy, by jako pierwszy odezwał się mędrzec stojący na miejscu numer 2 i by wymienił kolor jedynej czapki, jaką widzi przed sobą. Wtedy po minucie mędrzec na miejscu 1 powtarza jego wypowiedź (poprawnie określając kolor swojej czapki). Następnie mędrzec na miejscu 4 podaje kolor czapki bezpośrednio przed sobą, a właściciel tej czapki powtarza za nim, etc. Tę próbę na pewno przeżyją przynajmniej wszyscy mędrcy stojący na miejscach o numerach nieparzystych (oprócz, być może, ostatniego).

Dość łatwo można tę strategię poprawić tak, by przeżywało na pewno dwóch mędrców z każdej trójki: mędrzec numer 3 zaczyna, mówiąc „biała”, jeśli widzi przed sobą dwie identyczne czapki, oraz „czarna”, jeśli widzi różne. Następnie odzywa się mędrzec 2 – widzi czapkę mędrca 1 i wie, czy ma na głowie taką samą, czy inną, więc poprawnie określa jej kolor. Wtedy może zabrać głos mędrzec 1, który zna już kolor czapki mędrca 2 i wie, czy ma taką samą. Dalej zabierają głos mędrcy z kolejnej trójki (o numerach 6, 5, 4) i tak dalej.

Te strategie wciąż są jednak bardzo dalekie od optymalnej. Jak dobra może ona być? Na pewno nie da się zapewnić bezpieczeństwa temu spośród mędrców, który odzywa się jako pierwszy, ponieważ nie ma on żadnych informacji, pozwalających określić kolor własnej czapki. Ale, jak widać z powyższych przykładów, każdy odzywający się mędrzec, oprócz ratowania własnego życia, może przekazywać towarzyszom niedoli informacje o kolorach ich czapek. Może zatem warto, by jako pierwszy odzywał się mędrzec stojący na końcu (bo widzi najwięcej)? Wiemy już, że potrafi on uratować kolegę stojącego przed nim, a nawet dwóch. Może jest w stanie pomóc trzem lub jeszcze większej liczbie?

Rozwiązanie, czyli strategia optymalna

Okazuje się, że mędrzec z końca (odzywający się jako pierwszy) może swoją wypowiedzią uratować wszystkich innych!

Jak to działa? Mędrzec stojący na końcu mówi „biała”, jeśli widzi przed sobą nieparzystą liczbę białych czapek, a „czarna” – w przeciwnym przypadku. Jako następny odzywa się mędrzec stojący bezpośrednio przed nim. Sprawdza parzystość liczby białych czapek, które widzi. Jeśli zgadza się ona z parzystością podaną przez stojącego za nim mędrca, to oznacza, że sam ma na głowie czarną czapkę, a jeśli się nie zgadza – że ma na głowie „brakującą” białą. Umie zatem określić kolor własnej czapki! Deklaruje go, gwarantując sobie przeżycie. Teraz stojący przed nim mędrzec liczy, ile widzi białych czapek; wie, jaka parzystość ma wyjść w sumie (z punktu widzenia ostatniego mędrca) oraz jaką czapkę ma na głowie stojący za nim przedmówca, więc wylicza, jaką sam ma. I tak dalej – wszyscy przeżyją, być może poza nieszczęśnikiem, którego ustawiono na końcu (i który odzywał się jako pierwszy).

A jak to działa, jeśli król wkłada mędrcom na głowy czapki w trzech lub więcej kolorach? Tak samo! Dla 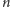 różnych kolorów ponumerujmy je liczbami 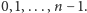 Mędrzec stojący na końcu dodaje wszystkie odpowiadające kolejnym czapkom liczby i podaje wynik modulo  (oczywiście deklarując stosowny kolor). Wtedy mędrzec stojący przed nim sumuje liczby odpowiadające czapkom, które widzi, i sprawdza, jaką liczbę trzeba dodać, by uzyskać właściwy wynik. W ten sposób wylicza, jaką czapkę ma na głowie. I tak dalej – znowu każdy mędrzec, gdy przychodzi jego kolej, zlicza to, co widzi, wie też, jakie czapki mają mędrcy stojący za nim (oprócz ostatniego) i jaka ma wyjść suma, więc wylicza, jaką czapkę sam ma na głowie.

Okazuje się zatem, że dla dowolnie wielu kolorów – przy tej, optymalnej, strategii – swoim życiem ryzykuje tylko ten mędrzec, którego uratować i tak się nie da, bo odzywa się jako pierwszy. Jeśli jednak ma szczęście, to wymieniony przez niego kolor okaże się właściwy i on również przeżyje. Czyli wymyślony przed groźnego króla sprawdzian nawet w pozornie jeszcze trudniejszej, wielokolorowej wersji, nie jest dla mędrców taki straszny!

Zagadkę tę opowiedział mi profesor Victor Ufnarovski z Uniwersytetu w Lund (Szwecja).