Wielkie granie
Gra hex i punkty stałe
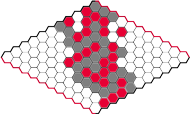
Hex jest jedną z najprostszych i jednocześnie jedną z najciekawszych z matematycznego punktu widzenia gier planszowych. Rozgrywka heksa jest prowadzona na romboidalnej planszy złożonej z sześciokątnych pól. Najbardziej typowe są plansze 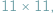 jak na rysunku, ale można grać na dowolnie dużej planszy.
jak na rysunku, ale można grać na dowolnie dużej planszy.
Reguły gry
Gracze na przemian stawiają na wolnym polu jeden pionek, kolorowy lub szary. Celem gracza I jest połączenie przeciwległych czarnych krawędzi za pomocą łańcucha szarych pionków, jak na rysunku. Taki łańcuch pionków będziemy nazywali wygrywającym dla gracza I. Gracz II chce zbudować łańcuch wygrywający łączący krawędzie kolorowe.
Remisy
Łatwo zaobserwować, że łańcuch wygrywający całkowicie izoluje od siebie krawędzie przeciwnika. Zatem nie mogą istnieć jednocześnie wygrywające łańcuchy dla szarych i kolorowych. A co będzie, jeśli po całkowitym wypełnieniu planszy żaden z graczy nie ma wygrywającego łańcucha? Pokażemy, że taka sytuacja nie może mieć miejsca. Innymi słowy, partia heksa nie może zakończyć się remisem.

Rozważmy przykładową planszę heksa. Dla wygody dodajmy sztuczne rzędy pól wzdłuż krawędzi planszy i oznaczmy skrajne punkty planszy literami: 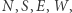 jak na rysunku obok.
jak na rysunku obok.
Rozpoczynając w punkcie 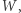 poruszajmy się po krawędziach między polami według następującej reguły. Na każdym rozgałęzieniu wybierzmy tę z dwóch krawędzi, która oddziela pola różnego koloru. Za każdym razem istnieje dokładnie jeden dobry wybór. Wyobraźmy sobie, że dochodzimy do pewnego rozgałęzienia. Przypuśćmy, że po lewej stronie mamy pole szare, a po prawej kolorowe (tak jak na pierwszym rozgałęzieniu, w wierzchołku
poruszajmy się po krawędziach między polami według następującej reguły. Na każdym rozgałęzieniu wybierzmy tę z dwóch krawędzi, która oddziela pola różnego koloru. Za każdym razem istnieje dokładnie jeden dobry wybór. Wyobraźmy sobie, że dochodzimy do pewnego rozgałęzienia. Przypuśćmy, że po lewej stronie mamy pole szare, a po prawej kolorowe (tak jak na pierwszym rozgałęzieniu, w wierzchołku 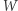 ). Jeśli pole przed nami jest szare, to skręcamy w prawo, jeśli jest kolorowe, to skręcamy w lewo. Zwróćmy uwagę, że dzięki temu zawsze po lewej stronie mamy pola szare, a po prawej kolorowe.
). Jeśli pole przed nami jest szare, to skręcamy w prawo, jeśli jest kolorowe, to skręcamy w lewo. Zwróćmy uwagę, że dzięki temu zawsze po lewej stronie mamy pola szare, a po prawej kolorowe.
Postępując w ten sposób, nigdy nie wrócimy do wierzchołka, w którym już byliśmy. Przypuśćmy przeciwnie, że doszliśmy do wierzchołka już raz odwiedzonego i że jest to pierwszy taki moment w naszej wędrówce. W takim razie musieliśmy dojść do niego krawędzią, której przedtem nie używaliśmy. Ale krawędź taka zawsze leży między polami tego samego koloru, więc nie mogliśmy jej wybrać - sprzeczność.

Plansza do heksa jest skończona, więc w końcu musimy z niej wyjść. Do dyspozycji mamy jedynie drogi przez 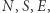 gdyż wszystkie inne wiodą między polami tego samego koloru.
gdyż wszystkie inne wiodą między polami tego samego koloru.
Jeśli ścieżka skończy się w wierzchołku 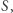 jak to ma miejsce na rysunku powyżej, to wyznacza wygrywający łańcuch dla szarych. Analogicznie, jeśli ścieżka dotrze do wierzchołka
jak to ma miejsce na rysunku powyżej, to wyznacza wygrywający łańcuch dla szarych. Analogicznie, jeśli ścieżka dotrze do wierzchołka 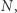 to wyznacza wygrywający łańcuch dla kolorowych. Zwróćmy uwagę, że ścieżka nie może opuścić planszy przez wierzchołek
to wyznacza wygrywający łańcuch dla kolorowych. Zwróćmy uwagę, że ścieżka nie może opuścić planszy przez wierzchołek 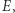 bo musielibyśmy minąć kolorowe pole po lewej, a szare po prawej.Uwaga!
bo musielibyśmy minąć kolorowe pole po lewej, a szare po prawej.Uwaga!
Strategie
Istnieje sprytna metoda, która pozwala na wykazanie, że w grze hex gracz, który zaczyna (czyli szary), ma strategię wygrywającą. Metoda ta polega na podkradaniu strategii przeciwnikowi. Przypuśćmy, że wygrywającą strategię ma gracz II. Gracz I powinien rozpocząć od zupełnie dowolnego ruchu, a następnie postępować tak, jak nakazuje hipotetyczna strategia gracza II, zamieniając miejscami kolory. Jedyny kłopot, jaki może się pojawić, to sytuacja, w której podkradziona strategia nakazuje zająć pole, na którym już stoi pionek. Może się to zdarzyć tylko wtedy, gdy jest to pionek postawiony podczas rozpoczynającego, losowego ruchu (w przeciwnym przypadku strategia nie wskazałaby tego pola). Wtedy ponownie wykonujemy dowolny możliwy ruch. Jest jasne, że posiadanie dodatkowego pionka na planszy nie pogarsza sytuacji gracza, zatem podkradziona strategia gwarantuje zwycięstwo pierwszemu graczowi. W ten sposób otrzymujemy sprzeczność z założeniem o istnieniu strategii dla drugiego gracza.
Powyższe rozumowanie jest całkowicie niekonstruktywne, nie daje graczowi I żadnych wskazówek odnośnie tego, jak powinien grać. Rozwiązanie tego problemu w praktyce jest bardzo trudne. Dotychczas udało się wyliczyć strategię dla planszy o rozmiarze 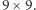 Mimo to, żeby zniwelować ewidentną przewagę gracza I, zaawansowani gracze dodają dodatkową regułę zamiany. Po tym, jak gracz I postawi pierwszy pionek, gracz II może zdecydować, czy będzie grał kolorowymi, czy szarymi. W ten sposób teoretycznie istnieje strategia wygrywająca dla gracza II, ale w praktyce gra staje się wystarczająco sprawiedliwa.
Mimo to, żeby zniwelować ewidentną przewagę gracza I, zaawansowani gracze dodają dodatkową regułę zamiany. Po tym, jak gracz I postawi pierwszy pionek, gracz II może zdecydować, czy będzie grał kolorowymi, czy szarymi. W ten sposób teoretycznie istnieje strategia wygrywająca dla gracza II, ale w praktyce gra staje się wystarczająco sprawiedliwa.

Dualna plansza
Czy hex może się przydać matematykowi do czegoś poza rozrywką? Okazuje się, że ta prosta gra ma głęboki związek z topologią. Żeby to dokładniej wyjaśnić, zastąpimy planszę do heksa przez planszę dualną. Na planszy dualnej pola reprezentowane są przez wierzchołki. Wierzchołki reprezentujące sąsiednie pola łączymy krawędzią. Dualną planszę 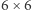 przedstawia rysunek.
przedstawia rysunek.
W tej interpretacji gracze stawiają pionki na wierzchołkach i usiłują zbudować ścieżkę łączącą przeciwległe krawędzie kwadratu. Nietrudno zauważyć, że jest to inny opis tej samej gry i wszystko, co powiedzieliśmy o heksie, jest prawdą również dla tej wersji.
Twierdzenie o punkcie stałym
Pokażemy teraz, jak wykorzystać grę hex na dualnej planszy w dowodzie ważnego twierdzenia topologicznego zwanego twierdzeniem Brouwera. Głosi ono, że każde ciągłe przekształcenie kwadratu w siebie pozostawia pewien punkt na swoim miejscu. Jeśli oznaczymy przez 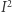 kwadrat
kwadrat ![|[0, 1] ×[0,1],](/math/temat/matematyka/gry_zagadki_paradoksy/2011/06/13/Gra_hex_i_punkty_stale/2x-ccf146aff64900a8de082cf37b34166bff8123fd-im-33,33,33-FF,FF,FF.gif) to twierdzenie powyższe można sformułować następująco: dla dowolnego ciągłego przekształcenia
to twierdzenie powyższe można sformułować następująco: dla dowolnego ciągłego przekształcenia 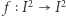 istnieje taki punkt
istnieje taki punkt 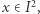 że
że 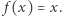 Taki punkt nazywamy punktem stałym przekształcenia
Taki punkt nazywamy punktem stałym przekształcenia 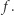 Zauważmy najpierw, że wystarczy udowodnić, że istnieje ciąg punktów
Zauważmy najpierw, że wystarczy udowodnić, że istnieje ciąg punktów 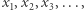 należących do
należących do 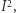 spełniających warunek:
spełniających warunek:

Rzeczywiście, kwadrat 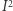 jest zbiorem domkniętym i ograniczonym, zatem z takiego ciągu
jest zbiorem domkniętym i ograniczonym, zatem z takiego ciągu 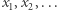 można wybrać podciąg
można wybrać podciąg 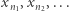 zbieżny do pewnego punktu
zbieżny do pewnego punktu 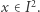 Z nierówności trójkąta otrzymujemy
Z nierówności trójkąta otrzymujemy

Obie odległości dążą do zera, więc granicą ciągu 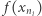 jest punkt
jest punkt  Jednocześnie z ciągłości funkcji
Jednocześnie z ciągłości funkcji 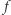 wynika, że
wynika, że 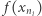 dąży do
dąży do 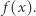 Zatem
Zatem 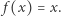 Spróbujmy więc wykazać istnienie takiego ciągu. Ustalmy
Spróbujmy więc wykazać istnienie takiego ciągu. Ustalmy 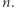 Wybierzmy
Wybierzmy 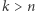 i tak duże, żeby spełniony był warunek:
i tak duże, żeby spełniony był warunek:
- jeśli
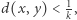 to
to 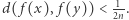
Podzielmy kwadrat 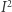 tak, aby otrzymać dualną planszę do gry hex o rozmiarze
tak, aby otrzymać dualną planszę do gry hex o rozmiarze 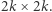 Przyjmijmy
Przyjmijmy 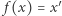 oraz
oraz 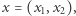
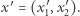 Przez
Przez 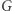 będziemy oznaczali zbiór wierzchołków, które pod wpływem
będziemy oznaczali zbiór wierzchołków, które pod wpływem 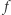 przesuwają się w górę o co najmniej
przesuwają się w górę o co najmniej 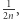 to znaczy
to znaczy 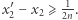 Podobnie definiujemy zbiory
Podobnie definiujemy zbiory 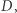
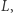
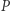 jako zbiory wierzchołków, które przesuwają się o co najmniej
jako zbiory wierzchołków, które przesuwają się o co najmniej 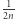 odpowiednio, w dół, w lewo i w prawo; przy czym do zbiorów
odpowiednio, w dół, w lewo i w prawo; przy czym do zbiorów 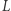 i
i 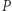 kwalifikujemy tylko te wierzchołki, które nie trafiły ani do
kwalifikujemy tylko te wierzchołki, które nie trafiły ani do 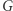 ani do
ani do 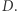
Ustalmy wierzchołki 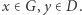 W takim razie,
W takim razie,

Jeśli  i
i 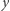 są połączone krawędzią, to ich pionowe współrzędne
są połączone krawędzią, to ich pionowe współrzędne 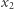 i
i 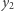 różnią się co najwyżej o
różnią się co najwyżej o 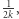 a zatem
a zatem

Dodając powyższe trzy nierówności stronami, dostajemy

Stąd odległość między 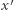 a
a 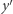 wynosi co najmniej
wynosi co najmniej 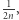 to jednak jest sprzeczne z tym, że wierzchołki
to jednak jest sprzeczne z tym, że wierzchołki  i
i 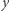 są połączone krawędzią. Jeśli bowiem dwa wierzchołki sąsiadują ze sobą, to odległość między nimi wynosi najwyżej
są połączone krawędzią. Jeśli bowiem dwa wierzchołki sąsiadują ze sobą, to odległość między nimi wynosi najwyżej 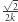 (długość skośnej krawędzi na planszy dualnej), zatem na mocy wyboru liczby
(długość skośnej krawędzi na planszy dualnej), zatem na mocy wyboru liczby 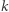 odległość między ich obrazami musi być ostro mniejsza niż
odległość między ich obrazami musi być ostro mniejsza niż 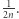 Wykazaliśmy więc, że wierzchołki ze zbiorów
Wykazaliśmy więc, że wierzchołki ze zbiorów 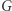 i
i 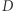 nie mogą sąsiadować. Oczywiście, wierzchołki ze zbioru
nie mogą sąsiadować. Oczywiście, wierzchołki ze zbioru 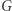 nie mogą leżeć na górnej krawędzi planszy, bo stamtąd nie da się pójść do góry. Podobnie wierzchołek ze zbioru
nie mogą leżeć na górnej krawędzi planszy, bo stamtąd nie da się pójść do góry. Podobnie wierzchołek ze zbioru 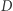 nie może leżeć na dolnej krawędzi planszy. W takim razie zbiór
nie może leżeć na dolnej krawędzi planszy. W takim razie zbiór 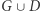 nie może zawierać łańcucha wygrywającego dla gracza chcącego połączyć górną i dolną krawędź. Podobnie
nie może zawierać łańcucha wygrywającego dla gracza chcącego połączyć górną i dolną krawędź. Podobnie 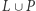 nie może zawierać łańcucha wygrywającego dla drugiego gracza. Skoro na planszy do gry w hex nie może być układu remisowego, to
nie może zawierać łańcucha wygrywającego dla drugiego gracza. Skoro na planszy do gry w hex nie może być układu remisowego, to 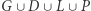 nie może wyczerpywać wszystkich wierzchołków planszy. Weźmy dowolny wierzchołek
nie może wyczerpywać wszystkich wierzchołków planszy. Weźmy dowolny wierzchołek 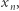 leżący poza
leżący poza 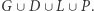 Z definicji zbiorów
Z definicji zbiorów 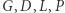 wynika, że obraz wierzchołka
wynika, że obraz wierzchołka 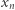 jest zawarty w kwadracie o środku
jest zawarty w kwadracie o środku 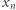 i krawędzi
i krawędzi 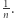 Zatem obraz
Zatem obraz 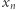 jest odległy od
jest odległy od 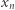 najwyżej o
najwyżej o 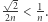 Podobny dowód z użyciem zwykłej szachownicy można znaleźć w Delcie 9/1980 (zadania 232-4).
Podobny dowód z użyciem zwykłej szachownicy można znaleźć w Delcie 9/1980 (zadania 232-4).
Inny dowód twierdzenia Brouwera, także w wyższych wymiarach, Czytelnik może znaleźć w znakomitych książkach Co to jest matematyka? oraz Dowody z księgi.