W planie poszczególne dni są przedstawione jako kwadraty siatki sześcianu, więc można było tę siatkę wyciąć i skleić.

Pozostałą część powierzchni strony frontalnej i całą stronę odwrotną zajmował algorytm układania kostki Rubika – będącej wówczas powszechnym obłędem.

Ciekawe są też napisy drobną czcionką: jeden z nich obwieszcza, że wydaliśmy ten plan w nakładzie 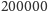 egzemplarzy (to nie pomyłka – dwieście tysięcy).

Ale powróćmy do algorytmu. Był on przedstawiony w postaci ikonek symbolizujących poszczególne ruchy – jak widać, byliśmy przygotowani na korzystanie z niego przez analfabetów. Chciałbym przypomnieć tutaj ten algorytm, nie korzystając z tego ułatwienia – opiszę go za pomocą symboli literowych.

Umówmy się, że litera  oznaczać będzie obrót o 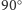 zgodnie z ruchem wskazówek zegara, a 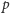 – przeciwnie (patrząc na tekst, jak na rysunku). Będziemy też używać litery 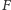 na oznaczenie ściany frontowej, 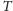 – tylnej, 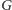 – górnej, 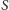 – środkowej (poziomej), 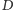 – dolnej, 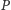 – prawej i 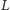 – lewej. Zatem np. 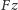 oznacza obrót ściany frontowej o 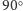 zgodnie z ruchem wskazówek zegara.

A oto jaki zaproponowaliśmy wtedy algorytm.

Na wejściu mamy kostkę z ułożoną pierwszą (dolną) warstwą.

---

Drugą można ułożyć, posługując się ruchami przedstawionymi poniżej:

---

Są już ułożone dwie warstwy. Żadna z dalszych kombinacji ruchów nie psuje tego, co zostało przed nią ułożone.

W ten sposób można obracać kostki na krawędziach (zawsze po dwie):

---

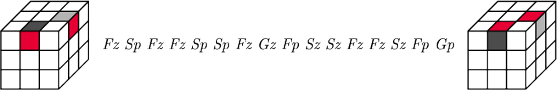
A w ten sposób je zamieniać (po trzy):

---

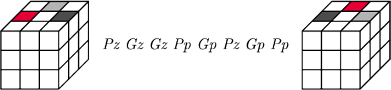
Tak zamienia się narożniki (też po trzy):

---

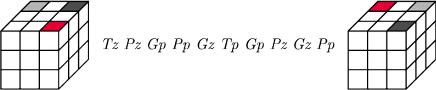
A tak się narożniki obraca (znów po dwa):

---

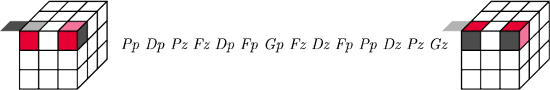
To wystarczy do ułożenia kostki Rubika.