Najpierw uszeregowali wszystkich od najsilniejszego do najsłabszego za pomocą turnieju „na rękę”. Następnie ustalili takie reguły. Najsilniejszy z nich proponuje metodę podziału i określa, kto ma dostać ile dukatów. Propozycja ta jest głosowana i jeśli uzyska co najmniej 50%, staje się ostateczna. Jeśli natomiast większość będzie przeciwko tej propozycji, to pozostali piraci wyrzucają proponenta za burtę do wody pełnej rekinów, a do głosu dochodzi najsilniejszy z pozostałych, który zgłasza kolejną propozycję podziału. Czynności te powtarza się dopóty, dopóki propozycja aktualnie najsilniejszego pirata nie zostanie zaakceptowana.

Piraci działają racjonalnie. Przede wszystkim będą zgłaszać propozycje, które nie spowodują ich kąpieli pośród rekinów. Po drugie, w ramach wszystkich propozycji bezpiecznych dla ich życia będą tak działać, aby zmaksymalizować swój zysk. Po trzecie w końcu, piraci są złośliwi i jeśli mają przy głosowaniu dwie równoważne z ich punktu widzenia decyzje, to ze względu na nabrzmiałe zadry będą głosować przeciwko proponentowi. Oczywiście piraci są rozsądnie myślącymi ludźmi i nie robią błędów logicznych, jeśli chodzi o życie lub pieniądze.

Spróbujmy znaleźć optymalne strategie dla proponentów, przy założeniu że mamy 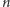 piratów. Dla 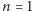problem się trywializuje. Jedyny pirat bierze wszystko i głosuje za tą propozycją. Podobnie jest dla 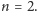Silniejszy z dwóch piratów decyduje, że bierze całe 100 dukatów, a ten słabszy nie jest w stanie go przegłosować. Przy 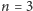najsilniejszy pirat (nazwijmy go Trójką) nie może wziąć całości, bo Dwójka na pewno zagłosuje przeciwko – przecież gdy Trójka polegnie, wówczas Dwójka zgarnie za chwilę 100 dukatów. Jedynce niby jest wszystko jedno – tak czy siak nie dostanie nic – ale zgodnie z regułą złośliwości zagłosuje przeciwko, bo przynajmniej pozbędzie się silnego oponenta. Zatem Trójka musi przekupić jednego z pozostałych. Dwójki przekupić nie sposób, ale jedynkę wystarczy zbyć jednym dukatem, aby zyskać w nim sojusznika. Zatem Trójka powinien zachować sobie 99 dukatów i dać Jedynce jednego dukata.

Z Czwórką jest podobnie. Powinien zyskać jednego sojusznika – potrzebuje dwóch głosów włącznie z własnym. Wystarczy więc przekupić Dwójkę, który by dostał figę z makiem, gdyby do głosu doszedł Trójka. Zatem optymalna strategia dla Czwórki to wziąć sobie 99 dukatów, a jednego dukata odpalić Dwójce, który choć zgrzytając zębami, ale zagłosuje za tą propozycją, zapewniając Czwórce zwycięskie 50%. (Jedynki dukat od Czwórki nie interesuje, bo i tak dostałby go od Trójki.)

Piątka musi mieć dwóch sojuszników. Widać, że wystarczy (i konieczne jest) przekupić minimalnym kosztem Jedynkę i Trójkę. Daje im zatem po jednym dukacie, a sobie pozostawia 98. Szóstka robi podobnie, tyle że obdarowuje Dwójkę i Czwórkę, bo Jedynka i Trójka wolą dostać dukata od Piątki i będą głosować przeciwko, nawet gdyby im zaproponował po dukacie. Piątka będzie głosował przeciwko każdej propozycji poniżej 98 dukatów. Zatem za pomocą dwóch dukatów Szóstka może się tylko w ten sposób obronić.

Wyłania się zatem prosty schemat. Jeżeli najsilniejszy pirat ma numer parzysty, to powinien dać po jednym dukacie wszystkim parzystym mniejszym od niego, a jeśli ma nieparzysty, to należy rozdać po jednym dukacie mniejszym nieparzystym, a sobie wziąć resztę.

Metoda ta działa, póki starczy dukatów. Co będzie jednak, gdy zbliżymy się do 200? Pirat 200 jeszcze coś zarobi, bo rozda 99 dukatów (po jednym) piratom o numera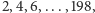ch a sobie weźmie ostatniego. Pirat 201 już nie zarobi, ale przeżyje: wystarczy, jeśli obdaruje po dukacie piratów o numerach 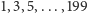– jest ich stu, a sobie nic nie zostawi. Każdy inny manewr niechybnie kończy się kąpielą. Tu co prawda 201 nie zarobi, ale żyć będzie, a to najważniejsze. Oczywiście nieparzyści będą głosować za, bo wiedzą, że jeśli do głosu dorwie się pirat 200, to nie mają na co liczyć. A ich głosy plus głos 201 dają wymarzoną przewagę. Pirat 202 analogicznie przeżywa, nic nie biorąc sobie i obdarowując mniejszych parzystych, których jest dokładnie 100.

Co z piratem 203? Nieszczęśnik nie ma szans. Potrzebuje 102 głosów. Poza sobą więc musi zjednać 101 zwolenników, a wszak parzyści, których jest 101, nie będą go popierali; zgodnie z regułą złośliwości wolą dostać swoją dolę od 202. Nie będzie go też popierał pirat 201 – on i tak nie ma szans na choćby jednego dukata, a wszak może koledze zaszkodzić…Zatem murowane 102 głosy pirat 203 ma przeciwko sobie.

Na pierwszy rzut oka wygląda na to, że od tej pory wszyscy piraci o numerach większych nie będą mieli szans przeżycia. Potrzebują przecież ponad stu zwolenników, a nie mają tylu dukatów, żeby ich przekupywać. Że tak nie jest, można się przekonać już przy piracie 204. Potrzebuje 102 głosów. I uzyska je! Jeden własny, 100 przekupionych oraz głos 203! Przecież dla 203 jedyną szansą na przeżycie jest poprzeć kogoś silniejszego: on nie może sobie pozwolić na to, żeby samemu decydować, bo polegnie! Kogo zatem ma przekupić 204? Oczywiście wszystkich nieparzystych 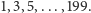Oni wszak wiedzą, że jeśli nie poprą tej decyzji, to polegnie najpierw 204, potem 203, a 202 rozda po dukacie parzystym i na tym się cała zabawa skończy.

Co dalej? Pirat 205 potrzebuje 103 głosów. Tym razem nie może liczyć ani na 203, ani na 204, którzy czują się już bezpiecznie. Nie ma więc biedak szans. Podobnie pirat 206 może liczyć co najwyżej na 102 głosy: stu przekupionych, 205 i swój. Pirat 207 ma co prawda dwóch desperatów: 205 i 206, ale wraz z własnym głosem i stoma cieniasami nie uzyska wymaganych 104 głosów. Dopiero pirat 208, mając na uwadze głosy 205, 206, 207 i swój plus umiejętnie przekupione płotki, może się czuć bezpiecznie. Oczywiście nic nie zarobi, bo 100 dukatów będzie musiał rozdać 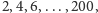ale uzyska wymarzone 50%, czyli 104 głosy.

Dla 209 sytuacja znów wygląda beznadziejnie. Ani 203, ani 204, ani żaden z 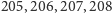 nie ma powodu, żeby go poprzeć – z chwilą gdy problem sprowadzi się do 208, wszyscy oni spokojnie przeżywają, więc kolegi 209 należy się pozbyć. Od tej pory do następnego szczęśliwego, który przeżyje, 209 będzie głosował za każdą propozycją. Podobnie zresztą jak 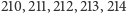i 215 – każdemu z nich będzie brakowało przynajmniej jednego głosu wśród słabszych od niego desperatów. Dopiero pirat 216 ma szansę. Potrzebnych mu 108 głosów dostarczy stu nieparzystych 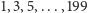plus siedmiu desperatów 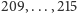i on sam. Zauważmy, że nierozsądne byłoby rozdanie po dukacie parzystym, którzy w tej sytuacji głosowaliby przeciwko – i tak swoją dolę dostaną od 208.

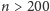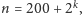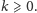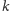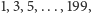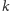Mamy już ogólny schemat: dla przeżywają tylko piraci o numerach gdzie Każdy taki pirat powinien rozdać sto dukatów stu słabeuszom o identycznej parzystości: dla parzystego nieparzystym, a dla nieparzystego parzystym

Jakie morały płyną z tej historii?
Po pierwsze: nie zawsze opłaca się być najlepszym.
Po drugie: ludzie zdesperowani bywają cenni.
Po trzecie: ciężki i niebezpieczny jest chleb pirata!