Jeden dwóch graczy, którego dalej będziemy nazywać Odpowiadającym, w tajemnicy przed drugim graczem (nazywanym Pytającym) wybiera liczbę naturalną nie większą od 1 000 000 (i oczywiście nie mniejszą od 1). Następnie Pytający zadaje kolejno 20 pytań dotyczących pomyślanej liczby. Pytania te muszą być jednak tak sformułowane, by dopuszczały jedynie odpowiedzi TAK lub NIE.

Pozornie pytania takie mogą być bardzo różne. „Czy pomyślana liczba jest mniejsza od 27?”. „Czy jest parzysta?”. „Czy jest liczbą pierwszą?”. „Czy mieści się między 23 i 456 lub między 1287 i 56007?”. „Czy jest to jedna z liczb 1475, 2964, 41994, 846711?”. Jeżeli się wszelkim takim pytaniom przyjrzeć, można zauważyć, że są one zawsze pytaniami o to, czy pomyślana liczba jest elementem pewnego, dowolnie wybranego przez Pytającego, podzbioru 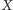przedziału

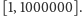
Odpowiadający za każdym razem udziela odpowiedzi zgodnej z prawdą. Po zadaniu 20 pytań Pytający musi odgadnąć pomyślaną liczbę: wymienia jedną z liczb od 1 do 1 000 000 i wygrywa wtedy i tylko wtedy, gdy jest to liczba wybrana na początku przez Odpowiadającego.

W grze w 20 pytań Pytający ma strategię wygrywającą, czyli istnieje taki sposób zadawania pytań, by niezależnie od tego, jaką liczbę wybrał Odpowiadający, liczbę tę odnaleźć.

Strategia, o której mowa, jest bardzo prosta: w każdym momencie dzielimy zbiór, w którym może się znajdować wybrana przez Odpowiadającego liczba, na dwie, możliwie równe, części (a więc jedna z nich zawiera co najwyżej o jedną liczbę więcej od drugiej) i pytamy, czy wybrana liczba jest w którejś (dowolnie przez nas wybranej) z nich. Zamiast uzasadniać, że jest to wygrywająca strategia w grze w 20 pytań, wykażę ogólniejszą prawidłowość.

Zamiast liczb od 1 do 1 000 000 zajmijmy się liczbami od 1 do i zamiast 20 pytań niech będzie ich 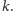Opisana strategia jest wygrywająca, gdy 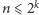; w przeciwnym razie Pytający strategii wygrywającej nie ma (i może wygrać tylko przypadkiem). Gdy to stwierdzenie uda się udowodnić, będziemy wiedzieli, że w grze w 20 pytań Pytający ma strategię wygrywającą – przecież 1 000

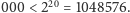
Najpierw uzasadnienie, że dla 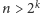nie ma wygrywającej strategii dla Pytającego. Wystarczy w tym celu podać sposób, w jaki może wygrać Odpowiadający. Sposób ten nazywa się strategią diabelską, choć strategią nie jest. Przecież Odpowiadający ma zawsze odpowiadać zgodnie z prawdą, więc w ogóle nie ma żadnej strategii. Chyba żeby …, no właśnie. Może nie wybrać żadnej liczby i odpowiadać na pytania najmniej korzystnie dla Pytającego.

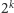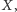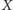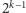Na początku jest więcej niż liczb. Jeśli Pytający zapyta, czy szukana przez niego liczba jest elementem zbioru to Odpowiadający mówi TAK, gdy w jest więcej liczb, niż w jego uzupełnieniu i NIE – w przeciwnym przypadku. W ten sposób wybiera tę odpowiedź, która jest mniej korzystna dla Pytającego (bo umiejscawia szukaną liczbę w większym zbiorze, a zatem mającym więcej niż elementów). Podobnie postępuje Odpowiadający, gdy otrzymuje kolejne pytania. Umiejscawia szukaną liczbę po dwóch pytaniach w zbiorze zawierającym więcej niż 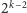liczb itd., aż po 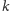pytaniach ma ją umiejscowioną w zbiorze zawierającym więcej niż 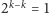liczbę, czyli co najmniej dwie liczby. Jakkolwiek zatem Pytający odgadywałby, zawsze może mu odpowiedzieć „źle” i wymienić, jako wybraną, inną liczbę.

Powiecie, że Odpowiadający oszukiwał. Zgoda, ale przecież mogłoby się zdarzyć, że rzeczywiście taką liczbę, jaką wymienił na końcu, wybrał na początku gry, a Pytający nie miał szczęścia i pytał zgodnie z tym, jak to Odpowiadający z góry przewidział. Z tego, co opowiadają o diable, wynika, że on mógłby to istotnie przewidzieć – stąd nazwa: strategia diabelska.

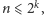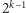Gdy jednak i diabeł Odpowiadającemu nie pomoże. Jeśli Pytający będzie pytał zgodnie z opisaną strategią, to nawet najgorsza dla niego możliwość będzie dopuszczała po pierwszym pytaniu umiejscowienie szukanej liczby w zbiorze zawierającym co najwyżej liczb, po drugim – 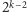liczb i wreszcie po 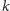pytaniach – w zbiorze zawierającym 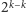liczb, czyli jedną liczbę. A więc Pytający wygra.

Nasuwa się pytanie – ile pytań musi mieć do dyspozycji Pytający, by na pewno wygrać, mimo że Odpowiadającemu pozwolimy raz skłamać ? Odpowiedź na to pytanie jest trudna, ale znana. Piszemy o niej w artykule „O grze w 20 pytań inaczej”.