Zadanie Alhazena»Zadanie 1
o zadaniu...
- Zadanie pochodzi z artykułu Zadanie Alhazena
- Publikacja w Delcie: czerwiec 2017
- Publikacja elektroniczna: 31 maja 2017
- Artykuł źródłowy w wersji do druku [application/pdf]: (56 KB)
Na okręgu o długości 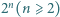 znajdują się punkty
znajdują się punkty 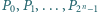 będące wierzchołkami
będące wierzchołkami 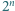 -kąta foremnego, oznaczone w taki sposób, że długość łuku
-kąta foremnego, oznaczone w taki sposób, że długość łuku 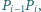 mierzonego zgodnie z ruchem wskazówek zegara, jest równa
mierzonego zgodnie z ruchem wskazówek zegara, jest równa 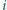 dla każdego
dla każdego 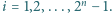 Niech
Niech

Udowodnić, że 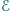 i
i 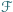 są przystające (jako podzbiory płaszczyzny).
są przystające (jako podzbiory płaszczyzny).
Twierdzenie (Pascala). Punkty 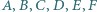 leżą na jednym okręgu. Proste
leżą na jednym okręgu. Proste 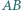 i
i 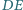 przecinają się w punkcie
przecinają się w punkcie 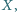 proste
proste 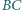 i
i 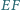 w punkcie
w punkcie 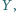 proste
proste 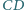 i
i 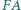 w punkcie
w punkcie 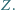 Wykaż, że wówczas punkty
Wykaż, że wówczas punkty 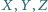 leżą na jednej prostej.
leżą na jednej prostej.
Okręgi 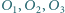 są styczne odpowiednio do par boków
są styczne odpowiednio do par boków 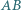 i
i 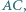
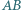 i
i 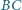 oraz
oraz 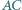 i
i 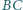 trójkąta
trójkąta 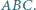 Okrąg
Okrąg 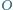 jest styczny zewnętrznie do okręgów
jest styczny zewnętrznie do okręgów 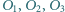 odpowiednio w punktach
odpowiednio w punktach 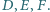 Wykaż, że proste
Wykaż, że proste 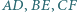 przecinają się w jednym punkcie.
przecinają się w jednym punkcie.
Dany jest równoległobok 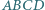 oraz punkt
oraz punkt 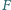 leżący na odcinku
leżący na odcinku 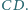 Punkty
Punkty 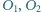 i
i 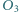 są środkami okręgów opisanych na trójkątach
są środkami okręgów opisanych na trójkątach 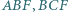 i
i 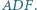 Dowieść, że ortocentrum trójkąta
Dowieść, że ortocentrum trójkąta 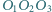 leży na prostej
leży na prostej 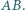
W czworokącie 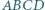 opisanym na okręgu prosta
opisanym na okręgu prosta 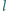 przechodząca przez wierzchołek
przechodząca przez wierzchołek 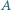 przecina bok
przecina bok 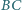 w punkcie
w punkcie 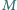 oraz półprostą
oraz półprostą 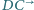 w punkcie
w punkcie 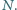 Punkty
Punkty 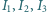 są środkami okręgów wpisanych odpowiednio w trójkąty
są środkami okręgów wpisanych odpowiednio w trójkąty 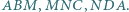 Dowieść, że punkt przecięcia wysokości trójkąta
Dowieść, że punkt przecięcia wysokości trójkąta 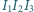 leży na prostej
leży na prostej 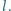
Dane są punkty 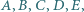 takie, że czworokąt
takie, że czworokąt 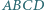 jest równoległobokiem, a czworokąt
jest równoległobokiem, a czworokąt 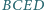 jest wpisany w okrąg. Prosta
jest wpisany w okrąg. Prosta 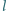 przechodząca przez
przechodząca przez 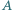 przecina wnętrze odcinka
przecina wnętrze odcinka 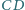 w punkcie
w punkcie 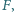 a prostą
a prostą 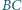 w punkcie
w punkcie 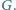 Przypuśćmy, że
Przypuśćmy, że 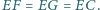 Wykazać, że
Wykazać, że 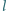 jest dwusieczną kąta
jest dwusieczną kąta 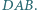
Dany jest trójkąt 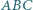 wpisany w okrąg
wpisany w okrąg 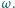 Punkt
Punkt 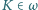 i punkt
i punkt 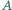 leżą po przeciwnych stronach prostej
leżą po przeciwnych stronach prostej 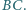 Punkty
Punkty 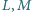 są odbiciami punktu
są odbiciami punktu 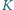 względem
względem 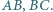 Okrąg przechodzący przez punkty
Okrąg przechodzący przez punkty 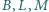 przecina
przecina 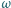 po raz drugi w punkcie
po raz drugi w punkcie 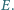 Punkt
Punkt 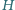 jest ortocentrum trójkąta
jest ortocentrum trójkąta 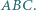 Wykazać, że proste
Wykazać, że proste 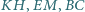 mają punkt wspólny.
mają punkt wspólny.
W trójkącie 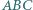 okrąg wpisany jest styczny do boków
okrąg wpisany jest styczny do boków 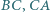 i
i 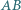 w punktach odpowiednio
w punktach odpowiednio 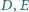 i
i 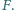 Punkt
Punkt 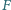 jest punktem Feuerbacha trójkąta
jest punktem Feuerbacha trójkąta 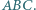 Wówczas prosta Simsona punktu
Wówczas prosta Simsona punktu 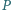 względem trójkąta
względem trójkąta 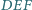 jest równoległa do prostej
jest równoległa do prostej 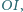 która łączy środki
która łączy środki 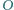 i
i 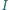 - okręgów opisanego i wpisanego trójkąta
- okręgów opisanego i wpisanego trójkąta 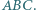
Punkty 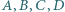 leżą kolejno na okręgu
leżą kolejno na okręgu 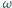 w taki sposób, że cięciwy
w taki sposób, że cięciwy 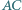 i
i 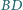 przecinają się pod kątem prostym. Obliczyć promień
przecinają się pod kątem prostym. Obliczyć promień  okręgu
okręgu 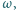 jeśli cięciwy
jeśli cięciwy 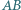 i
i 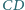 mają odpowiednio długości
mają odpowiednio długości 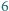 i
i 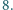
Na bokach 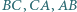 trójkąta
trójkąta 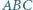 leżą punkty
leżą punkty 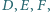 w których okręgi dopisane do trójkąta są styczne do tych boków. Niech
w których okręgi dopisane do trójkąta są styczne do tych boków. Niech 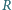 i
i  będą promieniami okręgów opisanego i wpisanego. Dowieść, że stosunek pól trójkątów
będą promieniami okręgów opisanego i wpisanego. Dowieść, że stosunek pól trójkątów 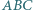 i
i 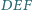 wynosi
wynosi 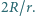
Przekątne czworokąta 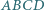 wpisanego w okrąg o środku
wpisanego w okrąg o środku 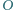 przecinają się w punkcie
przecinają się w punkcie 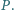 Niech
Niech 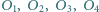 będą środkami okręgów opisanych odpowiednio na trójkątach
będą środkami okręgów opisanych odpowiednio na trójkątach 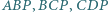 i
i 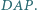 Wykazać, że proste
Wykazać, że proste 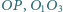 i
i 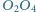 przecinają się w jednym punkcie.
przecinają się w jednym punkcie.
Sześciokąt 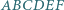 jest wpisany w okrąg i
jest wpisany w okrąg i 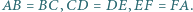 Wykaż, że główne przekątne tego sześciokąta przecinają się w jednym punkcie.
Wykaż, że główne przekątne tego sześciokąta przecinają się w jednym punkcie.
Odcinek 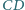 jest średnicą okręgu
jest średnicą okręgu 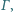 a cięciwa
a cięciwa 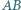 jest prostopadła do tej średnicy. Punkt
jest prostopadła do tej średnicy. Punkt 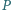 należy do krótszego łuku
należy do krótszego łuku 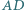 okręgu
okręgu 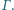 Proste
Proste 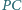 i
i 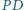 przecinają prostą
przecinają prostą 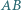 odpowiednio w punktach
odpowiednio w punktach 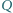 i
i 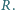 Wykaż, że
Wykaż, że 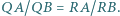
Udowodnij, że środek okręgu wpisanego w trójkąt jest ortocentrum trójkąta utworzonego przez środki okręgów dopisanych.
W trójkąt 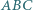 wpisany jest okrąg o promieniu
wpisany jest okrąg o promieniu 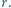 Proste styczne do okręgu i równoległe do boków trójkąta odcinają od niego trzy trójkąty. Wykaż, że suma promieni okręgów wpisanych w te trzy trójkąty jest równa
Proste styczne do okręgu i równoległe do boków trójkąta odcinają od niego trzy trójkąty. Wykaż, że suma promieni okręgów wpisanych w te trzy trójkąty jest równa 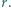
Trzy okręgi mają wspólny punkt, a pozostałe trzy punkty ich przecięć są współliniowe. Wykaż, że środki okręgów oraz ich wspólny punkt leżą na jednym okręgu.
Okrąg wpisany w trójkąt 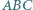 jest styczny do boków
jest styczny do boków 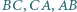 odpowiednio w punktach
odpowiednio w punktach 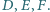 Prosta równoległa do
Prosta równoległa do 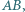 przechodząca przez punkt
przechodząca przez punkt 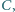 przecina proste
przecina proste 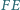 i
i 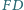 odpowiednio w punktach
odpowiednio w punktach 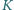 i
i 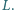 Udowodnij, że na czworokącie
Udowodnij, że na czworokącie 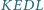 można opisać okrąg.
można opisać okrąg.
Czworokąt 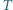 jest wpisany w okrąg
jest wpisany w okrąg 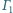 oraz opisany na okręgu
oraz opisany na okręgu 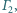 przy czym
przy czym 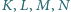 są kolejnymi punktami styczności
są kolejnymi punktami styczności 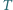 z
z 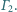 Wykaż, że
Wykaż, że