Okrąg Apoloniusza»Zadanie 4
o zadaniu...
- Zadanie olimpijskie: XXXVI OM
- Zadanie pochodzi z artykułu Okrąg Apoloniusza
- Publikacja w Delcie: styczeń 2013
- Publikacja elektroniczna: 01-01-2013
- Artykuł źródłowy w wersji do druku [application/pdf]: (83 KB)
Punkty
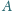 i
i
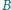 nie należą do płaszczyzny
nie należą do płaszczyzny
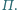 Wyznacz
zbiór wszystkich punktów
Wyznacz
zbiór wszystkich punktów
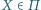 o tej własności, że proste
o tej własności, że proste
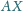 i
i
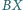 tworzą z płaszczyzną
tworzą z płaszczyzną
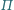 równe kąty.
równe kąty.
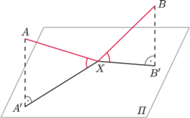
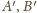 oznaczają odpowiednio rzuty punktów
oznaczają odpowiednio rzuty punktów
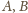 na
płaszczyznę
na
płaszczyznę
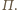 Dla punktu
Dla punktu
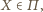 różnego od
różnego od
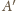 i
i
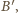 równość
równość
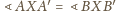 zachodzi wtedy i tylko
wtedy, gdy trójkąty prostokątne
zachodzi wtedy i tylko
wtedy, gdy trójkąty prostokątne
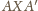 i
i
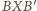 są podobne.
Równoważnie,
są podobne.
Równoważnie,
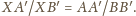 Jeśli
Jeśli
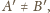 to
punkty
to
punkty
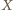 o żądanej własności tworzą okrąg Apoloniusza dla
punktów
o żądanej własności tworzą okrąg Apoloniusza dla
punktów
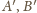 i stałej
i stałej
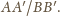 Jakie jest rozwiązanie, gdy
Jakie jest rozwiązanie, gdy
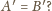 Czy możliwe, by
Czy możliwe, by
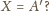
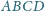 miara kąta wewnętrznego przy wierzchołku
miara kąta wewnętrznego przy wierzchołku
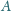 jest większa od
jest większa od
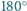 oraz zachodzi równość
oraz zachodzi równość
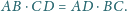 Punkt
Punkt
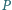 jest symetryczny do punktu
jest symetryczny do punktu
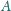 względem prostej
względem prostej
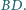 Udowodnij, że
Udowodnij, że
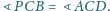
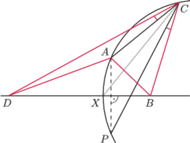
 i
i
 leżą na okręgu Apoloniusza dla punktów
leżą na okręgu Apoloniusza dla punktów
 i stałej
i stałej
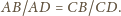 Z symetrii względem prostej
Z symetrii względem prostej
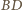 punkt
punkt
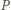 też na nim leży (
też na nim leży (
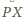 i
i
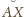 są równe, więc
są równe, więc
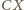 jest dwusieczną kąta
jest dwusieczną kąta
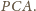 Jednocześnie
Jednocześnie
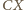 jest też dwusieczną kąta
jest też dwusieczną kąta
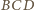 (własność z początku artykułu,
(własność z początku artykułu, 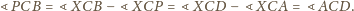
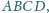 w którym
w którym
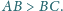 Na boku
Na boku
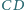 tego prostokąta skonstruuj takie punkty
tego prostokąta skonstruuj takie punkty
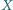 i
i
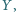 aby
aby
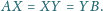
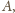 środka boku
środka boku
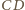 i stałej 2.
i stałej 2.
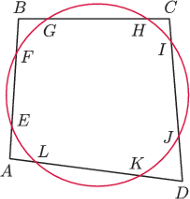
 przecina boki
przecina boki
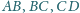 i
i
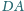 czworokąta
wypukłego
czworokąta
wypukłego
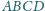 w punktach
w punktach
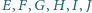 oraz
oraz
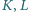 (patrz rysunek 3). Wykaż, że na czworokącie
(patrz rysunek 3). Wykaż, że na czworokącie
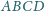 można opisać
okrąg wtedy i tylko wtedy, gdy suma długości łuków
można opisać
okrąg wtedy i tylko wtedy, gdy suma długości łuków
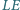 i
i
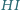 jest równa sumie długości łuków
jest równa sumie długości łuków
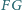 i
i
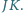
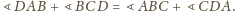 Z faktu
wnioskujemy, że
Z faktu
wnioskujemy, że
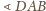 jest równy różnicy kątów wpisanych
w okrąg
jest równy różnicy kątów wpisanych
w okrąg
 i opartych na łukach
i opartych na łukach
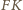 oraz
oraz
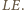 Podobnie
Podobnie
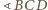 jest równy różnicy kątów wpisanych opartych na łukach
jest równy różnicy kątów wpisanych opartych na łukach
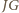 oraz
oraz
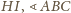 jest równy różnicy kątów wpisanych opartych
na łukach
jest równy różnicy kątów wpisanych opartych
na łukach
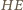 i
i
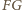 i
i
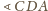 jest równy różnicy
kątów wpisanych opartych na łukach
jest równy różnicy
kątów wpisanych opartych na łukach
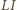 i
i
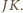 Oznaczmy przez
Oznaczmy przez
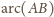 długość łuku
długość łuku
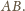 Zatem teza zadania zachodzi wtedy
i tylko wtedy, gdy
Zatem teza zadania zachodzi wtedy
i tylko wtedy, gdy
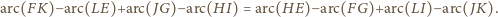
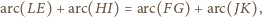
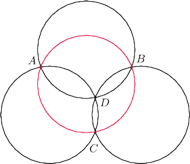
 mają dokładnie jeden punkt
wspólny
mają dokładnie jeden punkt
wspólny
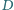 i przecinają się parami jeszcze w punktach
i przecinają się parami jeszcze w punktach
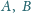 i
i
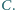 Udowodnić, że okrąg wyznaczony przez punkty
Udowodnić, że okrąg wyznaczony przez punkty
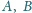 i
i
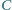 również ma promień długości
również ma promień długości
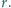
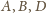 ;
;
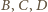 ;
;
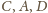 odpowiednio przez
odpowiednio przez
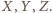 Niech
Niech
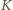 będzie takim punktem, że
będzie takim punktem, że
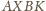 jest rombem. Zauważmy,
że czworokąty
jest rombem. Zauważmy,
że czworokąty
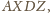
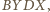
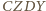 są rombami
o boku długości
są rombami
o boku długości
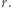 Wobec tego
Wobec tego
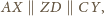 a z definicji
punktu
a z definicji
punktu
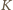 zachodzi
zachodzi
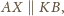 więc
więc
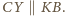 Ponieważ
są to odcinki długości
Ponieważ
są to odcinki długości
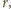 to także
to także
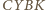 jest rombem
o boku długości
jest rombem
o boku długości
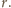 Zatem
Zatem
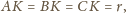 czyli punkty
czyli punkty
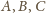 leżą na okręgu o środku w punkcie
leżą na okręgu o środku w punkcie
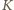 i promieniu
i promieniu
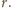
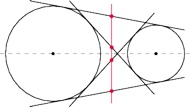
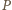 odcinka pomiędzy punktami styczności
odcinka pomiędzy punktami styczności
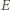 i
i
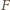 ma jednakową potęgę
ma jednakową potęgę
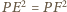 względem każdego
z okręgów, więc leży na ich osi potęgowej.
względem każdego
z okręgów, więc leży na ich osi potęgowej.
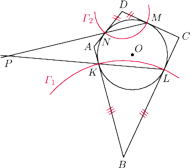
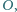 wpisany w czworokąt
wpisany w czworokąt
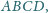 jest
styczny do boków
jest
styczny do boków
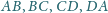 odpowiednio w punktach
odpowiednio w punktach
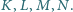 Proste
Proste
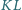 i
i
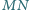 przecinają się w punkcie
przecinają się w punkcie
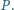 Wykaż, że proste
Wykaż, że proste
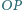 i
i
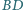 są prostopadłe.
są prostopadłe.
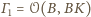 oraz
oraz
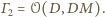 Prosta
Prosta
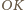 jest
styczna do
jest
styczna do
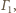 bo
bo
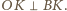 Stąd
Stąd
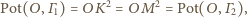
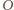 leży na osi potęgowej
leży na osi potęgowej
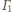 i
i
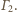 Ponadto
Ponadto
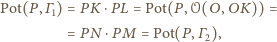
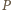 także leży na osi potęgowej
także leży na osi potęgowej
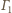 i
i
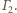 Oś potęgowa
Oś potęgowa
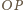 okręgów
okręgów
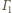 i
i
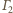 jest prostopadła do prostej
jest prostopadła do prostej
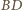 łączącej ich środki.
łączącej ich środki.
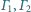 są współśrodkowe. Wykaż, że nie istnieje taki
punkt
są współśrodkowe. Wykaż, że nie istnieje taki
punkt
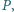 że
że
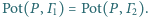
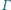 oraz punkty
oraz punkty
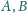 leżące w nierównych
odległościach od środka tego okręgu. Udowodnij, że wspólne cięciwy
okręgu
leżące w nierównych
odległościach od środka tego okręgu. Udowodnij, że wspólne cięciwy
okręgu
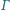 z okręgami przechodzącymi przez punkty
z okręgami przechodzącymi przez punkty
 i
i
 leżą na prostych mających jeden punkt wspólny.
leżą na prostych mających jeden punkt wspólny.
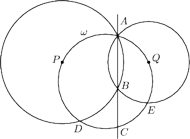
 i
i
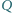 przecinają się w punktach
przecinają się w punktach
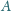 i
i
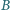 ; promienie
; promienie
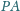 i
i
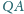 nie są prostopadłe. Okrąg opisany na
trójkącie
nie są prostopadłe. Okrąg opisany na
trójkącie
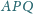 przecina te dwa okręgi w punktach
przecina te dwa okręgi w punktach
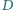 i
i
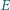 (różnych od
(różnych od
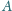 ) oraz przecina prostą
) oraz przecina prostą
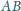 w punkcie
w punkcie
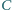 (różnym od
(różnym od
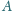 ). Dowieść, że okrąg opisany na trójkącie
). Dowieść, że okrąg opisany na trójkącie
 ma środek w punkcie
ma środek w punkcie
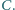
 opisany na trójkącie
opisany na trójkącie
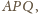 nie jest styczny do żadnego
z dwóch danych okręgów (bo je przecina w punktach różnych od
nie jest styczny do żadnego
z dwóch danych okręgów (bo je przecina w punktach różnych od
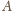 ).
Zatem żaden z odcinków
).
Zatem żaden z odcinków
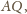
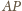 nie jest jego średnicą;
w takim razie żaden z kątów
nie jest jego średnicą;
w takim razie żaden z kątów
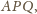
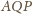 nie jest prosty. Stąd
wniosek, że żaden z punktów
nie jest prosty. Stąd
wniosek, że żaden z punktów
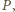
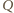 nie leży na prostej
nie leży na prostej
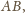 wobec czego prosta
wobec czego prosta
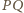 nie przechodzi przez punkt
nie przechodzi przez punkt
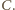
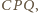 wpisany w okrąg
wpisany w okrąg
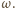 Wysokość poprowadzona z wierzchołka
Wysokość poprowadzona z wierzchołka
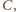 lub jej przedłużenie,
przecina okrąg
lub jej przedłużenie,
przecina okrąg
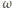 ponownie w punkcie
ponownie w punkcie
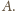 Ortocentrum trójkąta
Ortocentrum trójkąta
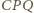 leży w punkcie symetrycznym do
leży w punkcie symetrycznym do
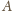 względem prostej
względem prostej
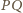 – czyli w punkcie
– czyli w punkcie
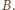
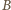 względem boków
względem boków
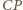 i
i
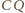 także leżą na okręgu
także leżą na okręgu
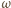 ; oznaczmy je odpowiednio przez
; oznaczmy je odpowiednio przez
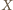 i
i
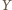 (żaden z nich nie pokrywa się z
(żaden z nich nie pokrywa się z
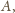 bo punkt
bo punkt
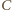 nie leży na prostej
nie leży na prostej
 ).
).
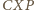 jest symetryczny do
jest symetryczny do
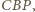 więc
więc
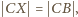
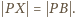 Ostatnia równość mówi, że
Ostatnia równość mówi, że
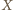 jest punktem okręgu o środku
jest punktem okręgu o środku
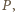 przechodzącego przez
przechodzącego przez
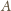 i
i
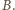 Skoro zaś leży na okręgu
Skoro zaś leży na okręgu
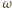 i nie pokrywa się z
i nie pokrywa się z
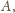 musi się pokrywać z
musi się pokrywać z
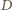 lub
lub
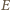 ; ustalmy oznaczenia (
; ustalmy oznaczenia (
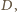
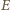 ) tak, że
) tak, że
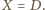 Analogicznie stwierdzamy,
że
Analogicznie stwierdzamy,
że
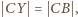
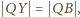
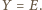 Tak więc
Tak więc
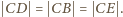 To znaczy, że punkty
To znaczy, że punkty
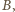
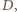
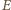 leżą
na okręgu o środku
leżą
na okręgu o środku
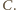
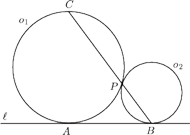
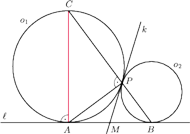
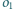 i
i
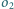 , styczne zewnętrznie w punkcie
, styczne zewnętrznie w punkcie
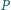 , są
styczne do prostej
, są
styczne do prostej
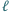 w punktach
w punktach
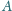 i
i
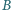 odpowiednio.
Prosta
odpowiednio.
Prosta
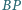 przecina okrąg
przecina okrąg
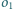 w punkcie
w punkcie
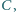 różnym
od
różnym
od
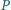 . Udowodnić, że proste
. Udowodnić, że proste
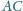 i
i
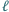 są prostopadłe.
są prostopadłe.
 okręgów
okręgów
 i
i
 przechodzącą przez punkt
przechodzącą przez punkt
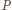 . Przecina ona prostą
. Przecina ona prostą
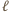 w punkcie
w punkcie
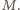 Ponieważ
Ponieważ
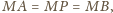 więc trójkąt
więc trójkąt
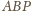 jest
prostokątny. Wobec tego
jest
prostokątny. Wobec tego
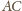 jest średnicą okręgu
jest średnicą okręgu
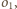 jako cięciwa,
na której oparty jest kąt prosty
jako cięciwa,
na której oparty jest kąt prosty
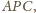 a średnica okręgu jest
prostopadła do stycznej w swoim końcu.
a średnica okręgu jest
prostopadła do stycznej w swoim końcu.
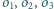 są rozłączne zewnętrznie. Te dwie styczne do
są rozłączne zewnętrznie. Te dwie styczne do
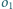 i
i
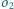 , które nie rozdzielają tych okręgów, przecinają się w punkcie
, które nie rozdzielają tych okręgów, przecinają się w punkcie
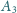 . Analogicznie definiujemy punkty
. Analogicznie definiujemy punkty
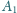 i
i
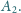 Wykaż, że
punkty
Wykaż, że
punkty
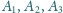 są współliniowe.
są współliniowe.
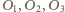 są na jednej prostej, to
są na jednej prostej, to
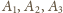 też na niej są.
Załóżmy więc, że środki okręgów nie są współliniowe. Płaszczyznę
zawierającą dane okręgi oznaczmy przez
też na niej są.
Załóżmy więc, że środki okręgów nie są współliniowe. Płaszczyznę
zawierającą dane okręgi oznaczmy przez
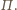 Niech punkty
Niech punkty
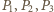 wszystkie leżą po jednej stronie płaszczyzny
wszystkie leżą po jednej stronie płaszczyzny
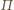 tak, że dla każdego i
rzutem punktu
tak, że dla każdego i
rzutem punktu
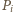 na
na
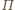 jest
jest
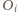 oraz
oraz
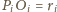 . Punkty
. Punkty
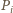 nie są współliniowe, bo
nie są współliniowe, bo
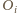 nie są. Niech
nie są. Niech
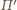 będzie
płaszczyzną wyznaczoną przez
będzie
płaszczyzną wyznaczoną przez
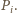 Nie jest ona równoległa do
Nie jest ona równoległa do
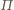 ,
bo ri są różne. Zatem
,
bo ri są różne. Zatem
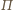 i
i
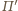 przecinają się wzdłuż pewnej
prostej.
przecinają się wzdłuż pewnej
prostej.
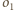 i
i
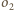 są jednokładne względem
są jednokładne względem
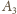 , więc
, więc
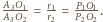 Stąd punkty
Stąd punkty
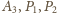 są współliniowe, czyli punkt
są współliniowe, czyli punkt
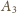 leży na płaszczyźnie
leży na płaszczyźnie
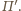 Leży też na
Leży też na
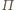 , więc należy
do ich wspólnej prostej. Analogicznie należą do niej punkty
, więc należy
do ich wspólnej prostej. Analogicznie należą do niej punkty
 i
i
 co kończy dowód.
co kończy dowód.
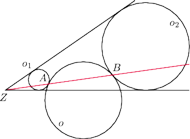
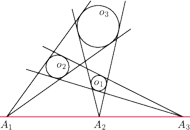
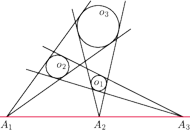
 i
i
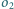 są rozłączne zewnętrznie i wpisane w kąt
o wierzchołku
są rozłączne zewnętrznie i wpisane w kąt
o wierzchołku
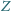 . Okrąg
. Okrąg
 jest styczny zewnętrznie do okręgów
jest styczny zewnętrznie do okręgów
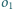 i
i
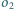 odpowiednio w punktach
odpowiednio w punktach
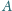 i
i
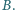 Udowodnij,
że punkty
Udowodnij,
że punkty
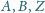 są współliniowe.
są współliniowe.
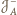 i
i
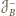 takie, że
takie, że
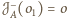 oraz
oraz
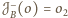 . Jednokładność
. Jednokładność
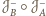 jest prosta oraz
jest prosta oraz
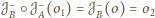 , więc jej środkiem musi być punkt
, więc jej środkiem musi być punkt
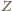 .
Leży on zatem na prostej
.
Leży on zatem na prostej
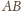 .
.
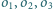 są rozłączne zewnętrznie. Te dwie styczne do
są rozłączne zewnętrznie. Te dwie styczne do
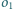 i
i
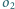 , które nie rozdzielają tych okręgów, przecinają się
w punkcie
, które nie rozdzielają tych okręgów, przecinają się
w punkcie
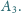 Analogicznie definiujemy punkty
Analogicznie definiujemy punkty
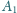 i
i
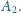 Wykaż, że punkty
Wykaż, że punkty
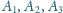 są współliniowe.
są współliniowe.
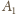 ,
,
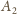 i
i
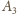 są środkami jednokładności
są środkami jednokładności
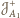 ,
,
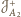 i
i
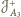 takich, że
takich, że
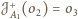 ,
,
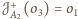 oraz
oraz
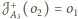 . Złożenie
. Złożenie
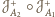 to jednokładność
prosta i
to jednokładność
prosta i
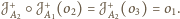 Stąd jej środkiem, który
na mocy twierdzenia musi leżeć na prostej
Stąd jej środkiem, który
na mocy twierdzenia musi leżeć na prostej
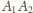 , jest na mocy faktu
punkt
, jest na mocy faktu
punkt
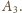
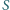 oraz punkt
oraz punkt
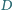 leżący na tym okręgu.
Cięciwa
leżący na tym okręgu.
Cięciwa
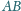 przecina odcinek
przecina odcinek
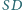 w punkcie
w punkcie
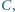 różnym od
punktu
różnym od
punktu
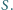 Wykaż, że
Wykaż, że
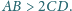
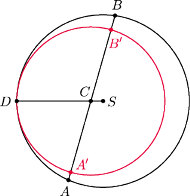
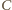 i promieniu
i promieniu
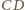 (czyli wewnętrznie
styczny do danego) – mamy wtedy
(czyli wewnętrznie
styczny do danego) – mamy wtedy
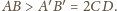 Prościej już chyba
nie można.
Prościej już chyba
nie można.