Delta mi!

Przedstawiamy wygodne narzędzie geometryczne o wielu zastosowaniach, wśród których znajduje się dowodzenie współliniowości punktów.

W Delcie 11/2017 został przedstawiony (bez dowodu) fakt, że dla czterech dowolnych prostych (tak dowolnych, że są parami nierównoległe i żadne trzy nie mają punktu wspólnego) ortocentra wyznaczonych przez nie czterech trójkątów leżą na jednej prostej, a okręgi opisane na tych trójkątach mają punkt wspólny. Ponadto parabola, której kierownicą jest prosta zawierająca ortocentra, a ogniskiem punkt wspólny okręgów opisanych jest styczna do czterech wyjściowych prostych (Rys. 1).

Odcinek 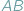widać z punktu 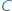pod kątem 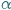, gdy 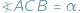Z twierdzenia o kątach wpisanych wynika, że jeśli punkty 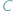i 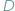leżą na okręgu po tej samej stronie jego cięciwy 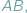to widać ją z 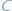i 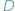pod tym samym kątem (Rys. 1).

Każdy zna twierdzenie o kącie zewnętrznym trójkąta: jest on równy sumie kątów wewnętrznych do niego nie przyległych (Rys. 1), co bierze się z faktu, że suma kątów przyległych jest równa sumie kątów trójkąta. Z twierdzenia tego wynika nietrudno twierdzenie o kącie wpisanym i środkowym: kąt wpisany jest równy 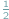kąta środkowego opartego na tym samym łuku.

Fakt (*). W trójkącie prostokątnym środek przeciwprostokątnej jest równo odległy od wierzchołków. Również na odwrót, jeśli środek okręgu opisanego leży na boku trójkąta, to trójkąt ten jest prostokątny.

Dany jest okrąg...

Gdy na lustrzaną sferę pada promień światła, odbija się on tak, że kąt między nim a przedłużeniem promienia sfery przechodzącego przez punkt, w którym promień pada, jest równy kątowi między tym przedłużeniem a promieniem odbitym, przy czym wszystko odbywa się w jednej płaszczyźnie wyznaczonej przez padający promień i środek sfery. Geometrycznie sytuacja jest więc dwuwymiarowa.

W niniejszym artykule przybliżymy własności jednej z najsłynniejszych prostych w geometrii euklidesowej - prostej Simsona. Jej odkrycie przypisywane jest szkockiemu matematykowi, Robertowi Simsonowi, choć w żadnej jego pracy nie znajdujemy wzmianki o niej.

Problem, który opiszę, został zaproponowany przez Amerykanów na LV Międzynarodową Olimpiadę Matematyczną, a jego treść brzmi następująco...

Jednym z najstarszych zagadnień matematyki są równania algebraiczne, wśród nich problem znalezienia pierwiastków trójmianu kwadratowego...

Przeciętny uczeń rozpoczyna podróż po fascynującym świecie geometrycznych konstrukcji uzbrojony w linijkę i kątomierz. Kiedy już nauczyciel uzna swojego podopiecznego za wystarczająco odpowiedzialnego, by nie rysował szkolnych ławek (jakże często zbyt naiwne założenie), uczeń dostaje do ręki kolejne narzędzie walki z czystą kartką papieru, jakim jest cyrkiel...

Istnieje zaskakujący związek między okręgiem wpisanym w trójkąt i okręgiem na nim opisanym.

Wiele wzorów na sumy kolejnych liczb naturalnych, ich kwadratów, sześcianów itp. można uzasadnić (lub przynajmniej przekonująco zilustrować) na rysunkach. Często rysunki te wymagają niewiele lub nawet zero komentarza – są to tzw. dowody bez słów...

W naszych rozważaniach wzbogacimy płaszczyznę o dodatkowy punkt, który oznaczymy przez 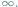 Przyjmiemy przy tym, że ów punkt leży na każdej z prostych. Takie rozszerzone proste oraz okręgi obejmiemy wspólną nazwą bloków...

...jeśli ma się 5 jego punktów. No, może trochę przesadziłem... Okręgu tak dosłownie nakreślić nie można, ale można narysować jego kolejnych kilka punktów, nawet gdy te kilka to np. 100 -- oczywiście, im większa będzie to liczba, tym dłużej będzie to trwało, bo rysować będziemy te punkty kolejno, po jednym.

Gdzie na płaszczyźnie znajdują się punkty, których stosunek odległości do dwóch ustalonych punktów 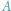 i 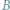 równy jest danej dodatniej stałej

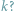
Matematycy od wielu lat zajmują się wędrówką po okręgu. Jednym z najbardziej znanych przykładów jest chyba skakanie po nim w określonym kierunku tak, by między kolejnymi punktami, w których się znajdziemy, była określona odległość  (mierzona wzdłuż łuku). Naturalne staje się wówczas pytanie, czy skacząc tak po okręgu, wrócimy kiedykolwiek do punktu wyjścia (widać, że rozwiązanie problemu nie zależy od punktu startowego)? Odpowiedź nasuwa się prędko – powrót nastąpi tylko wówczas, gdy stosunek długości okręgu do liczby  jest liczbą wymierną. Spróbujmy tym razem powędrować w inny sposób, określony geometrycznie.