Każdy trójkąt jest równoboczny»Zadanie 4
o zadaniu...
- Zadanie pochodzi z artykułu Każdy trójkąt jest równoboczny
- Publikacja w Delcie: grudzień 2014
- Publikacja elektroniczna: 01-12-2014
- Artykuł źródłowy w wersji do druku [application/pdf]: (84 KB)
Wyznacz pole elipsy, znając długości jej półosi.
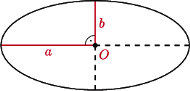
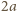 i
i 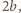 równoległych do jej półosi. Powinowactwo prostokątne o skali
równoległych do jej półosi. Powinowactwo prostokątne o skali 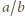 i o osi zawierającej dużą półoś elipsy przekształca nasz prostokąt na kwadrat, a elipsę na koło weń wpisane. Stąd stosunek pola
i o osi zawierającej dużą półoś elipsy przekształca nasz prostokąt na kwadrat, a elipsę na koło weń wpisane. Stąd stosunek pola 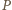 elipsy do pola
elipsy do pola 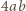 prostokąta równy jest stosunkowi pola koła do pola kwadratu na nim opisanego, czyli
prostokąta równy jest stosunkowi pola koła do pola kwadratu na nim opisanego, czyli 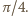 Wobec tego
Wobec tego 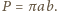
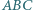 jest styczny do boków
jest styczny do boków 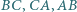 odpowiednio w punktach
odpowiednio w punktach 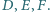 Udowodnij, że punkty
Udowodnij, że punkty 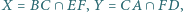
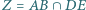 leżą na jednej prostej.
leżą na jednej prostej.
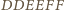 punkty
punkty 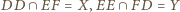 oraz
oraz 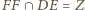 są współliniowe.
są współliniowe.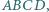 który nie jest trapezem, opisano okrąg. Wykaż, że punkty
który nie jest trapezem, opisano okrąg. Wykaż, że punkty 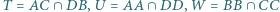 leżą na jednej prostej.
leżą na jednej prostej.
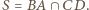 Z Twierdzenia Pascala dla sześciokąta
Z Twierdzenia Pascala dla sześciokąta 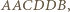 punkt
punkt 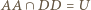 leży na prostej wyznaczonej przez punkty
leży na prostej wyznaczonej przez punkty 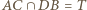 oraz
oraz 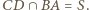 Z kolei z Twierdzenia Pascala dla
Z kolei z Twierdzenia Pascala dla 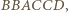 punkt
punkt 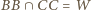 także leży na prostej wyznaczonej przez punkty
także leży na prostej wyznaczonej przez punkty 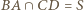 oraz
oraz 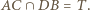
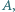
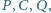
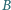 leżą w tej kolejności na łuku okręgu
leżą w tej kolejności na łuku okręgu 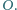 Na odcinkach
Na odcinkach 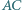 i
i 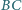 wybrano takie punkty odpowiednio
wybrano takie punkty odpowiednio 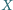 i
i 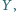 że
że 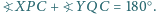 Wykaż, że wszystkie otrzymane w ten sposób proste
Wykaż, że wszystkie otrzymane w ten sposób proste 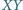 (przy ustalonych punktach
(przy ustalonych punktach 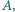
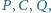
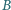 ) mają punkt wspólny.
) mają punkt wspólny.
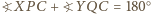 wynika, że punkt
wynika, że punkt 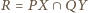 leży na okręgu
leży na okręgu 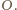 Z Twierdzenia Pascala dla sześciokąta
Z Twierdzenia Pascala dla sześciokąta 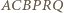 uzyskujemy współliniowość punktów
uzyskujemy współliniowość punktów 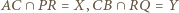 oraz niezależnego od
oraz niezależnego od 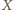 i
i 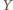 punktu
punktu 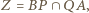 co kończy dowód.
co kończy dowód.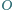 jest styczny do okręgu
jest styczny do okręgu 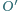 opisanego na trójkącie
opisanego na trójkącie 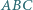 w punkcie
w punkcie 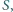 a do boków
a do boków 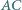 i
i 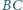 odpowiednio w punktach
odpowiednio w punktach 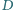 i
i 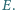 Wykaż, że środek okręgu wpisanego w trójkąt
Wykaż, że środek okręgu wpisanego w trójkąt 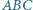 jest środkiem odcinka
jest środkiem odcinka 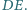
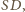
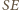 przecinają okrąg
przecinają okrąg 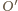 odpowiednio w drugich punktach
odpowiednio w drugich punktach 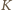 i
i 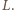 Warto rozważyć Twierdzenia Pascala dla sześciokąta
Warto rozważyć Twierdzenia Pascala dla sześciokąta 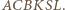
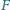 leży na boku
leży na boku 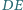 pięciokąta wypukłego
pięciokąta wypukłego 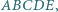 przy czym
przy czym 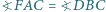 oraz
oraz 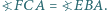 Wykaż, że
Wykaż, że 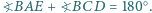
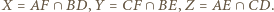
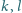 są styczne do okręgu
są styczne do okręgu
 w punktach
w punktach
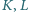 i przecinają
się w punkcie
i przecinają
się w punkcie
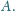 Punkt
Punkt
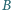 jest środkiem odcinka
jest środkiem odcinka
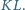 Wykazać, że punkty
Wykazać, że punkty
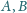 są symetryczne względem okręgu
są symetryczne względem okręgu
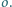
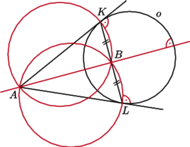
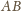 jest prostopadła do
jest prostopadła do
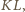 to jako bloki z definicji
można przyjąć okręgi o średnicach
to jako bloki z definicji
można przyjąć okręgi o średnicach
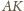 i
i
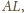 gdyż są
prostopadłe do
gdyż są
prostopadłe do
 i przechodzą przez
i przechodzą przez
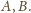 Oczywiście, sama
prosta
Oczywiście, sama
prosta
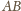 też się do tego celu nadaje.
też się do tego celu nadaje.
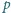 i
i
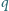 przecinają się w punktach
przecinają się w punktach
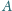 i
i
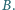 Prosta
Prosta
 jest styczna do tych okręgów w punktach odpowiednio
jest styczna do tych okręgów w punktach odpowiednio
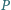 i
i
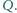 Punkt
Punkt
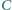 jest środkiem odcinka
jest środkiem odcinka
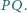 Wykazać,
że punkty
Wykazać,
że punkty
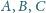 są współliniowe.
są współliniowe.

 będzie okręgiem o średnicy
będzie okręgiem o średnicy
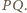 Okręgi
Okręgi
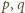 są
do niego prostopadłe, a zatem punkty
są
do niego prostopadłe, a zatem punkty
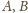 są symetryczne względem
są symetryczne względem
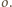 Stąd już wynika, że są współliniowe z punktem
Stąd już wynika, że są współliniowe z punktem
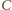 jako
środkiem tego okręgu – prosta poprowadzona z
jako
środkiem tego okręgu – prosta poprowadzona z
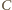 do punktu
do punktu
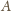 jest prostopadła do
jest prostopadła do
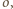 więc musi przechodzić przez punkt
więc musi przechodzić przez punkt
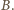
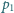 i
i
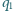 przecinają się w punktach
przecinają się w punktach
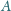 i
i
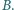 Prosta
Prosta
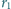 jest styczna do tych okręgów w punktach odpowiednio
jest styczna do tych okręgów w punktach odpowiednio
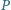 i
i
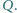 Punkt
Punkt
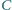 jest symetryczny do punktu
jest symetryczny do punktu
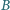 względem prostej
względem prostej
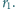 Okrąg
Okrąg
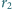 jest opisany na trójkącie
jest opisany na trójkącie
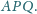 Proste
Proste
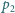 i
i
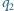 styczne do
styczne do
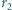 w punktach
odpowiednio
w punktach
odpowiednio
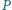 i
i
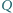 przecinają się w punkcie
przecinają się w punkcie
 Wykazać,
że punkty
Wykazać,
że punkty
 są współliniowe.
są współliniowe.
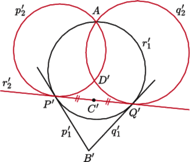
 ; obraz każdej z figur oznaczmy przez dodanie znaku prim. Na
podstawie własności 1 możemy zauważyć, że figury z zadania
zamieniły się rolami: okręgi
; obraz każdej z figur oznaczmy przez dodanie znaku prim. Na
podstawie własności 1 możemy zauważyć, że figury z zadania
zamieniły się rolami: okręgi
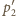 i
i
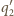 przecinają się w punktach
przecinają się w punktach
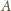 i
i
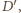 prosta
prosta
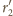 jest styczna do tych okręgów w punktach
jest styczna do tych okręgów w punktach
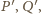 okrąg
okrąg
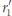 jest opisany na trójkącie
jest opisany na trójkącie
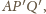 proste
proste
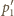 i
i
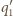 są styczne do
są styczne do
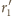 w punktach
w punktach
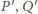 oraz
przecinają się w punkcie
oraz
przecinają się w punkcie
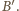
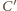 jest symetryczny do punktu
jest symetryczny do punktu
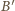 względem okręgu
względem okręgu
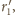 co na mocy zadania 1 oznacza, że jest
środkiem odcinka
co na mocy zadania 1 oznacza, że jest
środkiem odcinka
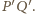 W ten sposób otrzymaliśmy konfigurację
z zadania 2, a zatem punkty
W ten sposób otrzymaliśmy konfigurację
z zadania 2, a zatem punkty
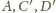 są współliniowe. Obrazem prostej
są współliniowe. Obrazem prostej
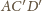 jest prosta
jest prosta
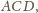 co kończy rozwiązanie.
co kończy rozwiązanie.
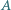 i
i 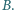 Punkt
Punkt 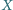 leży na jednym z tych okręgów, punkt
leży na jednym z tych okręgów, punkt 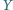 na drugim, przy czym prosta
na drugim, przy czym prosta 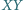 nie przechodzi ani przez
nie przechodzi ani przez 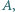 ani przez
ani przez 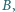 ani przez środek odcinka
ani przez środek odcinka 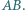 Punkt
Punkt 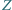 jest wierzchołkiem równoległoboku
jest wierzchołkiem równoległoboku 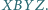 Dowieść, że okręgi opisane na trójkątach
Dowieść, że okręgi opisane na trójkątach 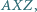
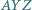 są przystające do dwóch danych okręgów.
są przystające do dwóch danych okręgów.
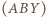 przez
przez 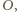 środek okręgu
środek okręgu 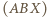 przez
przez 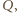 i niech
i niech 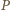 będzie punktem symetrycznym do
będzie punktem symetrycznym do 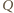 względem prostej
względem prostej 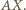 Czworokąty
Czworokąty 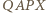 i
i 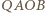 są rombami. Zatem
są rombami. Zatem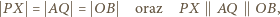
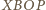 jest równoległobokiem. Również czworokąt
jest równoległobokiem. Również czworokąt 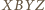 jest (z założenia) równoległobokiem. Stąd - jak przed chwilą - wnosimy, że równoległobokiem jest także czworokąt
jest (z założenia) równoległobokiem. Stąd - jak przed chwilą - wnosimy, że równoległobokiem jest także czworokąt 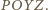 Wobec tego
Wobec tego 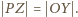
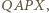 pokazuje, że odległość punktu
pokazuje, że odległość punktu 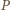 od każdego z trójki punktów
od każdego z trójki punktów 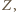
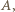
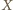 jest równa promieniowi dwóch danych okręgów. Inaczej mówiąc,
jest równa promieniowi dwóch danych okręgów. Inaczej mówiąc, 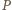 jest środkiem okręgu przystającego do nich i przechodzącego przez punkty
jest środkiem okręgu przystającego do nich i przechodzącego przez punkty 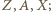 to jest pierwsza część tezy. Druga część tezy, dotycząca okręgu opisanego na trójkącie
to jest pierwsza część tezy. Druga część tezy, dotycząca okręgu opisanego na trójkącie 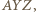 wynika z pierwszej przez symetrię (logiczną).
wynika z pierwszej przez symetrię (logiczną).
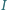 będzie środkiem okręgu wpisanego w trójkąt
będzie środkiem okręgu wpisanego w trójkąt
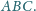 Półproste
Półproste
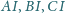 przecinają okrąg opisany na
nim odpowiednio w punktach
przecinają okrąg opisany na
nim odpowiednio w punktach
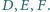 Udowodnić, że proste
Udowodnić, że proste
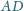 i
i
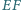 są prostopadłe.
są prostopadłe.

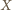 będzie punktem przecięcia prostych
będzie punktem przecięcia prostych
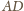 i
i
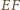 oraz
oraz
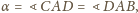
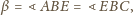
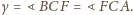
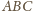 otrzymujemy
otrzymujemy
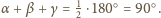 Ponadto kąty
Ponadto kąty
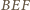 i
i
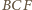 są oparte na tym samym łuku, a stąd
są oparte na tym samym łuku, a stąd
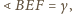 natomiast kąt
natomiast kąt
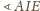 jako kąt zewnętrzny trójkąta
jako kąt zewnętrzny trójkąta
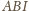 ma miarę
ma miarę
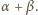 W takim razie
W takim razie
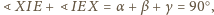 więc
trójkąt
więc
trójkąt
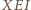 jest prostokątny.
jest prostokątny.
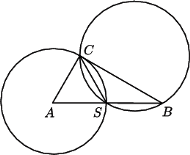
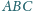 o kącie prostym przy wierzchołku
o kącie prostym przy wierzchołku
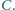 Okrąg o środku w punkcie
Okrąg o środku w punkcie
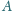 i promieniu
i promieniu
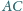 przecina
bok
przecina
bok
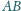 w punkcie
w punkcie
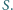 Udowodnić, że ten okrąg przystaje do
okręgu opisanego na trójkącie
Udowodnić, że ten okrąg przystaje do
okręgu opisanego na trójkącie
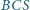 wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy
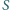 jest
środkiem
jest
środkiem
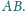
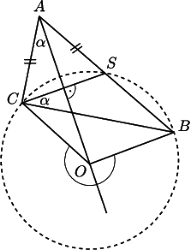
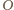 będzie środkiem okręgu opisanego na trójkącie
będzie środkiem okręgu opisanego na trójkącie
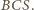 Ponieważ trójkąt
Ponieważ trójkąt
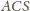 jest równoramienny, dwusieczna
kąta
jest równoramienny, dwusieczna
kąta
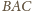 to symetralna odcinka
to symetralna odcinka
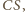 więc leży na niej punkt
więc leży na niej punkt
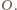 Oznaczmy
Oznaczmy
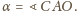 Wówczas
Wówczas
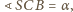 a skoro
a skoro
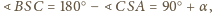 to
to
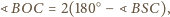
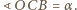 Równość
Równość
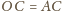 jest
równoważna
jest
równoważna
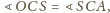 czyli
czyli
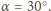 A to jest
równoważne temu, że
A to jest
równoważne temu, że
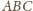 jest połówką trójkąta równobocznego
lub że
jest połówką trójkąta równobocznego
lub że
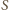 jest środkiem
jest środkiem
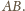
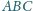 okrąg wpisany jest styczny do boków
okrąg wpisany jest styczny do boków
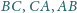 odpowiednio w punktach
odpowiednio w punktach
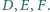 Punkty
Punkty
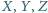 zostały obrane odpowiednio na bokach
zostały obrane odpowiednio na bokach
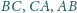 tak,
że
tak,
że
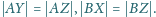 Dowieść, że prosta
Dowieść, że prosta
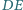 połowi
odcinek
połowi
odcinek

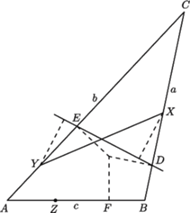
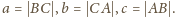 Równości
Równości
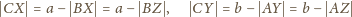
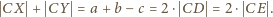
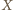 i
i
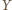 leżą po przeciwnych stronach
prostej
leżą po przeciwnych stronach
prostej
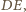 w jednakowych odległościach od odpowiednich końców
odcinka
w jednakowych odległościach od odpowiednich końców
odcinka
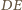 :
:
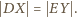
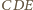 oznacza to z kolei, że
punkty
oznacza to z kolei, że
punkty
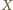 i
i
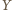 leżą w jednakowych odległościach od prostej
leżą w jednakowych odległościach od prostej
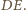 Stąd już wynika, że ta prosta przechodzi przez środek odcinka
Stąd już wynika, że ta prosta przechodzi przez środek odcinka
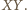
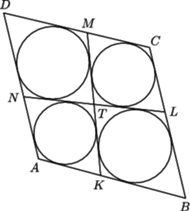
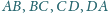 czworokąta wypukłego
czworokąta wypukłego
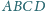 dane są
odpowiednio punkty
dane są
odpowiednio punkty
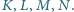 Odcinki
Odcinki
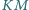 i
i
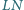 przecinają
się w punkcie
przecinają
się w punkcie
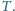 Udowodnić, że jeśli w każdy z czworokątów
Udowodnić, że jeśli w każdy z czworokątów
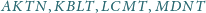 można wpisać okrąg, to w czworokąt
można wpisać okrąg, to w czworokąt
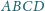 także.
także.
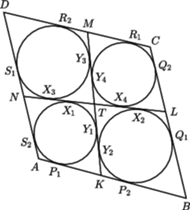
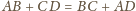 jest
równoważny
jest
równoważny
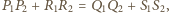 gdyż
gdyż
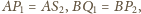
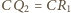 i
i
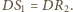 Zauważmy, że
Zauważmy, że
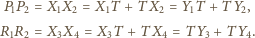
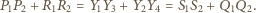
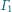 i
i
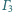 jest styczny zewnętrznie
do każdego z rozłącznych okręgów
jest styczny zewnętrznie
do każdego z rozłącznych okręgów
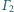 i
i
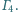 Wykaż, że punkty
styczności leżą na jednym okręgu.
Wykaż, że punkty
styczności leżą na jednym okręgu.
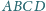 okręgi wpisane w trójkąty
okręgi wpisane w trójkąty
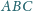 i
i
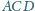 są styczne. Wykaż, że ich punkty styczności
z bokami czworokąta leżą na jednym okręgu.
są styczne. Wykaż, że ich punkty styczności
z bokami czworokąta leżą na jednym okręgu.
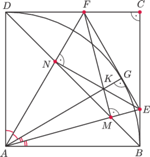
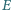 i
i
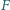 leżą odpowiednio na bokach
leżą odpowiednio na bokach
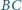 i
i
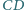 kwadratu
kwadratu
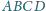 o boku 1, przy czym prosta
o boku 1, przy czym prosta
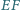 jest styczna do okręgu o środku
jest styczna do okręgu o środku
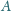 i promieniu 1. Proste
i promieniu 1. Proste
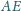 i
i
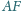 przecinają przekątną
przecinają przekątną
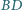 odpowiednio w punktach
odpowiednio w punktach
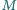 i
i
 Udowodnij, że punkty
Udowodnij, że punkty
 leżą na
jednym okręgu.
leżą na
jednym okręgu.
 będzie punktem styczności prostej
będzie punktem styczności prostej
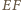 do danego
okręgu. Wtedy
do danego
okręgu. Wtedy
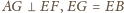 oraz
oraz
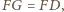 zatem
zatem
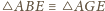 oraz
oraz
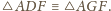 Stąd
Stąd
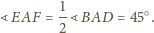
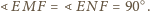
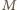 i
i
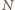 leżą na okręgu o średnicy
leżą na okręgu o średnicy
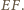 Leży na nim też punkt
Leży na nim też punkt
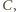 bo
bo
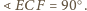
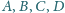 leżą, w tej właśnie kolejności, na prostej
leżą, w tej właśnie kolejności, na prostej
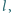 przy
czym
przy
czym
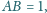
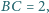
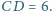 Rozstrzygnij, czy istnieje taki
punkt
Rozstrzygnij, czy istnieje taki
punkt
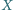 spoza prostej
spoza prostej
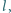 aby
aby
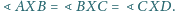

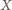 istnieje, to
istnieje, to
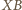 jest dwusieczną kąta
jest dwusieczną kąta
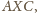 zatem z twierdzenia o dwusiecznej
zatem z twierdzenia o dwusiecznej
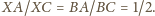 Punkty
Punkty
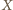 i
i
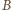 leżą więc na okręgu Apoloniusza dla punktów
leżą więc na okręgu Apoloniusza dla punktów
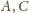 i stałej 1/2. Analogicznie punkty
i stałej 1/2. Analogicznie punkty
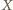 i
i
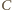 leżą na
okręgu Apoloniusza dla punktów
leżą na
okręgu Apoloniusza dla punktów
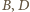 i stałej 1/3.
i stałej 1/3.

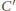 na prostej
na prostej
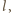 różny od
różny od
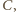 spełnia
warunek
spełnia
warunek
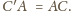 Wtedy
Wtedy
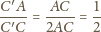
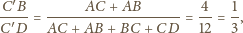
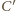 należy do obydwu powyższych okręgów. Średnicą
pierwszego z nich jest więc
należy do obydwu powyższych okręgów. Średnicą
pierwszego z nich jest więc
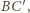 a drugiego –
a drugiego –
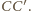 Stąd jedynym
ich wspólnym punktem jest
Stąd jedynym
ich wspólnym punktem jest
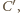 czyli
czyli
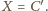 Ale wtedy
Ale wtedy
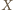 leży na prostej
leży na prostej
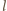 – sprzeczność.
– sprzeczność.
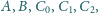 przy czym
przy czym
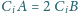 dla
dla
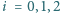 oraz
oraz
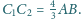 Udowodnij,
że kąt
Udowodnij,
że kąt
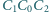 jest prosty i że punkty
jest prosty i że punkty
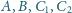 leżą na jednej
płaszczyźnie.
leżą na jednej
płaszczyźnie.

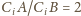 dla
dla
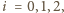 więc wszystkie punkty
więc wszystkie punkty
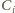 leżą na sferze Apoloniusza dla punktów
leżą na sferze Apoloniusza dla punktów
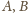 i stałej 2
(zdefiniowanej analogicznie do okręgu). Jej średnicę wyznaczają punkty
i stałej 2
(zdefiniowanej analogicznie do okręgu). Jej średnicę wyznaczają punkty
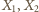 na prostej
na prostej
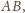 spełniające warunek
spełniające warunek
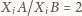 dla
dla
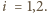 Wówczas
Wówczas
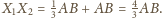
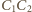 także jest średnicą rozważanej sfery. Stąd
kąt
także jest średnicą rozważanej sfery. Stąd
kąt
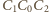 jest prosty, jako wpisany oparty na średnicy. Proste
jest prosty, jako wpisany oparty na średnicy. Proste
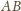 i
i
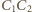 przecinają się (w środku sfery), więc punkty
przecinają się (w środku sfery), więc punkty
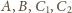 leżą na jednej płaszczyźnie.
leżą na jednej płaszczyźnie.