Styczna i cięciwa»Zadanie 3
o zadaniu...
- Zadanie pochodzi z artykułu Styczna i cięciwa
- Publikacja w Delcie: wrzesień 2015
- Publikacja elektroniczna: 31-08-2015
- Artykuł źródłowy w wersji do druku [application/pdf]: (79 KB)
Dany jest kwadrat 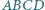 i taki punkt
i taki punkt 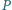 w jego wnętrzu, dla którego
w jego wnętrzu, dla którego 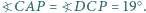 Wyznacz
Wyznacz 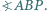
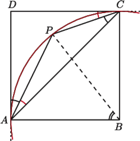
 prosta
prosta 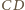 jest styczna do okręgu opisanego na trójkącie
jest styczna do okręgu opisanego na trójkącie 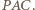 Wobec tego środek tego okręgu leży na prostej
Wobec tego środek tego okręgu leży na prostej 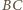 (bo
(bo 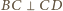 ). Analogicznie prosta
). Analogicznie prosta 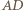 także jest styczna do tego okręgu, gdyż
także jest styczna do tego okręgu, gdyż 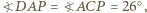 zatem środek rozważanego okręgu leży też na prostej
zatem środek rozważanego okręgu leży też na prostej 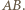 Stąd jest nim punkt
Stąd jest nim punkt 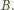
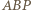 jest więc kątem środkowym opartym na tym samym łuku, co kąt wpisany
jest więc kątem środkowym opartym na tym samym łuku, co kąt wpisany 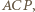 zatem
zatem 
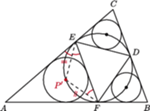
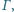 wpisany w trójkąt
wpisany w trójkąt 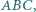 jest styczny do boków
jest styczny do boków 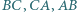 odpowiednio w punktach
odpowiednio w punktach 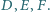 Wykaż, że środki
Wykaż, że środki 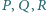 okręgów wpisanych w trójkąty
okręgów wpisanych w trójkąty 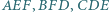 leżą na okręgu
leżą na okręgu 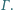
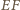 okręgu
okręgu 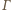 przez
przez 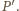 Wówczas
Wówczas 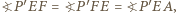 przy czym druga równość wynika z twierdzenia
przy czym druga równość wynika z twierdzenia 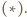 Wobec tego
Wobec tego 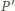 leży na dwusiecznej kąta
leży na dwusiecznej kąta 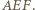 Analogicznie dla kąta
Analogicznie dla kąta 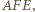 więc
więc 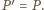 Dowód dla punktów
Dowód dla punktów 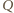 i
i 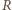 przebiega podobnie.
przebiega podobnie.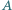 i
i 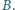 Proste styczne do tych okręgów w punkcie
Proste styczne do tych okręgów w punkcie 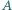 przecinają je w drugich punktach
przecinają je w drugich punktach 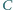 i
i 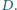 Wykaż, że
Wykaż, że 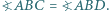
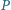 poprowadzono prostą przecinającą dany okrąg
poprowadzono prostą przecinającą dany okrąg 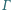 w punktach
w punktach 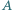 i
i 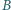 oraz prostą styczną do
oraz prostą styczną do 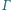 w punkcie
w punkcie 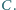 Wykaż, że
Wykaż, że 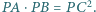
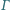 jest styczny do prostej
jest styczny do prostej 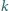 w punkcie
w punkcie 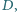 cięciwa
cięciwa 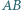 tego okręgu jest równoległa do
tego okręgu jest równoległa do 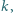 punkt
punkt 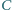 należy do prostej
należy do prostej 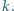 Proste
Proste 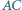 i
i 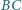 przecinają okrąg
przecinają okrąg 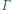 w drugich punktach
w drugich punktach 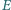 i
i 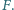 Wykaż, że prosta
Wykaż, że prosta 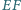 przechodzi przez środek odcinka
przechodzi przez środek odcinka 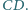
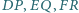 przecinają się w jednym punkcie
przecinają się w jednym punkcie 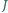 oraz że punkty
oraz że punkty 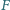 i
i 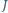 są symetryczne względem prostej
są symetryczne względem prostej 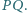
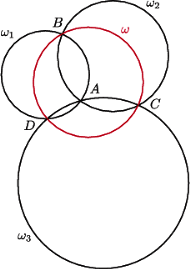
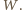 Wówczas istnieją w tym zbiorze okręgi
Wówczas istnieją w tym zbiorze okręgi 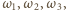 które mają punkt wspólny
które mają punkt wspólny 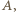 oraz okrąg
oraz okrąg 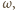 który nie przechodzi przez
który nie przechodzi przez 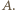 Oznaczmy punkty wspólne, różne od
Oznaczmy punkty wspólne, różne od 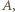 okręgów
okręgów 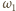 i
i 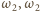 i
i 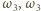 i
i 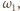 odpowiednio przez
odpowiednio przez 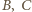 oraz
oraz 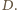 Wówczas
Wówczas 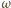 przechodzi przez wszystkie te punkty.
przechodzi przez wszystkie te punkty.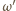 ze zbioru
ze zbioru 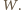 Musi on przechodzić przez
Musi on przechodzić przez 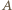 lub
lub 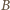 (ponieważ są to jedyne punkty wspólne okręgów
(ponieważ są to jedyne punkty wspólne okręgów 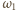 i
i 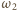 ). Podobnie okrąg
). Podobnie okrąg 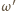 musi przechodzić przez co najmniej jeden z każdej pary punktów spośród
musi przechodzić przez co najmniej jeden z każdej pary punktów spośród 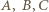 i
i 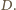 Stąd
Stąd 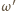 przechodzi przez co najmniej trzy z tych punktów. To jest jednak niemożliwe, bo każda taka trójka wyznacza jednoznacznie jeden z okręgów
przechodzi przez co najmniej trzy z tych punktów. To jest jednak niemożliwe, bo każda taka trójka wyznacza jednoznacznie jeden z okręgów 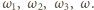
 oraz okrąg
oraz okrąg  o środku w punkcie
o środku w punkcie  Dla punktu
Dla punktu 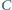 należącego do okręgu
należącego do okręgu 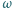 i nienależącego do prostej
i nienależącego do prostej 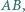 punkt
punkt 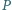 jest przecięciem prostej
jest przecięciem prostej 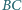 i dwusiecznej kąta
i dwusiecznej kąta 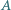 w trójkącie
w trójkącie 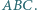 Wyznaczyć zbiór wszystkich otrzymanych w ten sposób punktów
Wyznaczyć zbiór wszystkich otrzymanych w ten sposób punktów 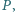 gdy
gdy 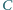 przebiega okrąg
przebiega okrąg 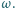

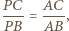 a skąd
a skąd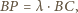
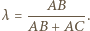
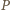 to obraz punktu
to obraz punktu 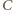 przy jednokładności o środku
przy jednokładności o środku 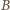 i skali
i skali 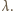 Poszukiwany zbiór punktów
Poszukiwany zbiór punktów 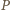 jest więc obrazem okręgu
jest więc obrazem okręgu 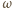 (bez dwóch punktów) przy tej jednokładności.
(bez dwóch punktów) przy tej jednokładności.
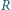 i
i  są styczne zewnętrznie. Poprowadzono ich wspólną styczną i w obszar ograniczony przez nią i okręgi wpisano okrąg. Ile wynosi jego promień?
są styczne zewnętrznie. Poprowadzono ich wspólną styczną i w obszar ograniczony przez nią i okręgi wpisano okrąg. Ile wynosi jego promień?
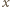 oznacza szukany promień. Jeden z trójkątów prostokątnych widocznych na rysunku ma przeciwprostokątną będącą sumą promieni o długościach
oznacza szukany promień. Jeden z trójkątów prostokątnych widocznych na rysunku ma przeciwprostokątną będącą sumą promieni o długościach 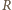 i
i  oraz przyprostokątną o długości
oraz przyprostokątną o długości 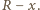 Z twierdzenia Pitagorasa otrzymujemy, że długość drugiej przyprostokątnej, a więc również długość odcinka pomiędzy odpowiednimi punktami styczności jest równa
Z twierdzenia Pitagorasa otrzymujemy, że długość drugiej przyprostokątnej, a więc również długość odcinka pomiędzy odpowiednimi punktami styczności jest równa 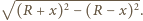
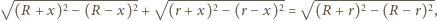
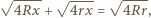
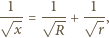
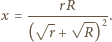
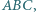 mając dany jego wierzchołek
mając dany jego wierzchołek 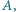 punkt
punkt 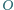 - środek okręgu opisanego i punkt
- środek okręgu opisanego i punkt 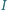 - środek okręgu wpisanego.
- środek okręgu wpisanego.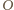 i promieniu
i promieniu 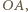
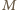 - jego punkt przecięcia z prostą
- jego punkt przecięcia z prostą 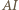 oraz okrąg o środku
oraz okrąg o środku 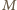 i promieniu
i promieniu 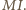 Na mocy twierdzenia
Na mocy twierdzenia 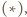 punkty przecięcia powyższych dwóch okręgów to wierzchołki
punkty przecięcia powyższych dwóch okręgów to wierzchołki 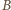 i
i 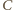 trójkąta.
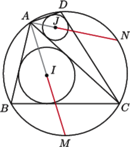
trójkąta.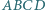 jest wpisany w okrąg
jest wpisany w okrąg 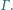 Punkt
Punkt 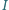 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 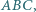 prosta
prosta 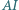 przecina okrąg
przecina okrąg 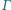 w punkcie
w punkcie 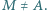 Punkt
Punkt 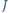 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 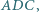 prosta
prosta 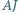 przecina okrąg
przecina okrąg 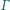 w punkcie
w punkcie 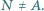 Wykaż, że jeżeli
Wykaż, że jeżeli 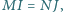 to
to 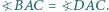
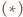 i założenia, zachodzi równość
i założenia, zachodzi równość 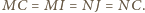 Stąd
Stąd 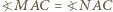 jako kąty wpisane w okrąg
jako kąty wpisane w okrąg 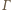 oparte na równych łukach. Wobec tego
oparte na równych łukach. Wobec tego 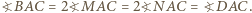
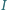 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 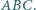 Wykaż, że okrąg opisany na trójkącie
Wykaż, że okrąg opisany na trójkącie 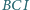 wyznacza na prostych
wyznacza na prostych 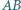 i
i 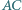 równe cięciwy.
równe cięciwy.
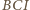 jest punkt
jest punkt 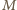 z twierdzenia
z twierdzenia 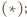 leży on na dwusiecznej kąta
leży on na dwusiecznej kąta 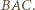 Z symetrii problemu okrąg ten wyznacza więc na ramionach kąta równe cięciwy.
Z symetrii problemu okrąg ten wyznacza więc na ramionach kąta równe cięciwy.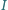 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 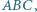 punkt
punkt 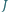 jest środkiem okręgu dopisanego do tego trójkąta. Wykaż, że środek odcinka
jest środkiem okręgu dopisanego do tego trójkąta. Wykaż, że środek odcinka 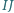 należy do okręgu opisanego na trójkącie
należy do okręgu opisanego na trójkącie 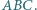
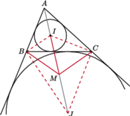
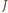 leży w kącie
leży w kącie 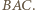 Dwusieczne kątów przyległych są prostopadłe, więc
Dwusieczne kątów przyległych są prostopadłe, więc 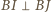 oraz
oraz 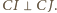 Wobec tego na czworokącie
Wobec tego na czworokącie 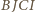 można opisać okrąg, którego środkiem jest środek
można opisać okrąg, którego środkiem jest środek 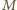 odcinka
odcinka 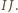 Okrąg ten jest opisany na trójkącie
Okrąg ten jest opisany na trójkącie 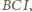 czyli
czyli 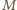 to punkt z twierdzenia
to punkt z twierdzenia 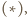 leży więc na okręgu opisanym na trójkącie
leży więc na okręgu opisanym na trójkącie 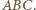
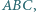 mając dane jego wierzchołki
mając dane jego wierzchołki 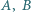 oraz promień okręgu wpisanego.
oraz promień okręgu wpisanego. jest styczny do okręgu opisanego na trójkącie
jest styczny do okręgu opisanego na trójkącie 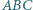 w punkcie
w punkcie 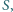 a do boków
a do boków 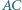 i
i 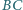 odpowiednio w punktach
odpowiednio w punktach 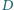 i
i 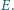 Wykaż, że jeśli
Wykaż, że jeśli 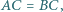 to środek okręgu wpisanego w trójkąt
to środek okręgu wpisanego w trójkąt 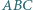 jest środkiem odcinka
jest środkiem odcinka 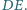
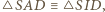 gdzie
gdzie 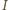 to środek odcinka
to środek odcinka 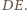

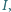 wpisany w trójkąt
wpisany w trójkąt 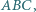 jest styczny do boku
jest styczny do boku 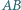 w punkcie
w punkcie 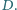 Punkt
Punkt 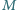 jest środkiem boku
jest środkiem boku 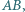 punkt
punkt 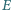 jest symetryczny do punktu
jest symetryczny do punktu 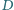 względem
względem 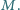 Udowodnić, że proste
Udowodnić, że proste 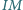 oraz
oraz 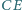 są równoległe.
są równoległe.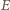 jest punktem styczności z bokiem
jest punktem styczności z bokiem 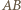 okręgu dopisanego do trójkąta
okręgu dopisanego do trójkąta 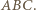 Jeżeli więc przez
Jeżeli więc przez 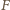 oznaczymy punkt środkowosymetryczny do
oznaczymy punkt środkowosymetryczny do 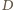 względem
względem 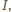 to jednokładność o środku w punkcie
to jednokładność o środku w punkcie 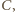 która przekształca okrąg wpisany na okrąg dopisany, przeprowadza punkt
która przekształca okrąg wpisany na okrąg dopisany, przeprowadza punkt 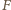 na punkt
na punkt 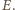 A zatem punkty
A zatem punkty 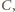
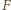 i
i 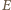 są współliniowe. Prosta
są współliniowe. Prosta 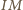 jest zatem prostą łączącą środki boków w trójkącie
jest zatem prostą łączącą środki boków w trójkącie 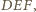 a stąd wynika żądana równoległość.
a stąd wynika żądana równoległość.
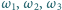 mają wspólny punkt
mają wspólny punkt 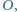 a ponadto
a ponadto 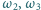 przecinają się jeszcze w punkcie
przecinają się jeszcze w punkcie 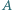 i podobnie
i podobnie 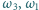 i
i 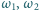 - w punkcie
- w punkcie 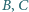 odpowiednio. Prosta
odpowiednio. Prosta 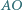 przecina
przecina 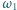 ponadto w punkcie
ponadto w punkcie 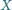 i podobnie
i podobnie 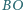 przecina
przecina 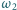 w
w 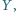 a
a 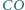 przecina
przecina 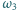 w
w 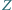 (rysunek). Udowodnić, że
(rysunek). Udowodnić, że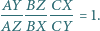
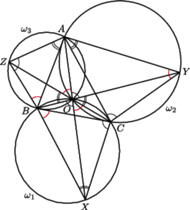
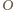 jak następuje:
jak następuje: 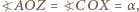
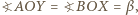
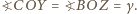
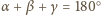 oraz na mocy tw. o kątach wpisanych,
oraz na mocy tw. o kątach wpisanych, 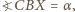
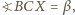 więc kąty w trójkącie
więc kąty w trójkącie 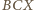 wynoszą
wynoszą 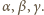 Analogicznie jest dla trójkątów
Analogicznie jest dla trójkątów 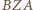 i
i 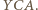 Zatem są to trójkąty podobne do trójkąta
Zatem są to trójkąty podobne do trójkąta 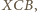 w szczególności
w szczególności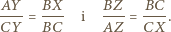
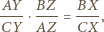
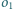 i
i 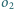 o środkach odpowiednio
o środkach odpowiednio 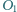 i
i 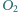 przecinają się w dwóch różnych punktach
przecinają się w dwóch różnych punktach 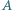 i
i 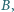 przy czym kąt
przy czym kąt 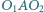 jest rozwarty. Prosta
jest rozwarty. Prosta 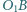 przecina okrąg
przecina okrąg 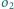 w punkcie
w punkcie 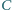 różnym od
różnym od 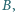 a prosta
a prosta 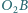 przecina okrąg
przecina okrąg 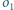 w punkcie
w punkcie 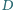 różnym od
różnym od 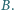 Wykazać, że punkt
Wykazać, że punkt 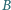 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 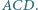
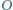 jest środkiem elipsy wpisanej w czworokąt
jest środkiem elipsy wpisanej w czworokąt 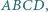 to
to
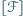 oznacza pole figury
oznacza pole figury 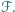
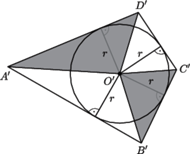
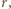 obrazem punktu
obrazem punktu 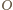 jest środek okręgu
jest środek okręgu 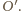 Czworokąt
Czworokąt 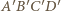 jest opisany na okręgu, zachodzi więc równość
jest opisany na okręgu, zachodzi więc równość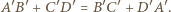
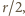 uzyskujemy tezę dla okręgu. Przekształcenia afiniczne zachowują równość pól, zatem teza zachodzi także dla wyjściowej elipsy.
uzyskujemy tezę dla okręgu. Przekształcenia afiniczne zachowują równość pól, zatem teza zachodzi także dla wyjściowej elipsy.