Potęga punktu względem okręgu»Zadanie 2
o zadaniu...
- Zadanie pochodzi z artykułu Potęga punktu względem okręgu
- Publikacja w Delcie: listopad 2019
- Publikacja elektroniczna: 31 października 2019
- Artykuł źródłowy w wersji do druku [application/pdf]: (417 KB)
Dany jest trapez 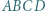 o podstawach
o podstawach 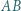 i
i 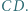 Okręgi o średnicach
Okręgi o średnicach 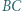 i
i 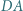 przecinają się w punktach
przecinają się w punktach 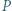 i
i 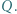 Przekątne trapezu przecinają się w punkcie
Przekątne trapezu przecinają się w punkcie 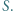 Dowieść, że punkty
Dowieść, że punkty 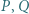 i
i 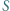 leżą na jednej prostej.
leżą na jednej prostej.
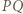 jest osią potęgową pary okręgów z zadania, więc wystarczy wykazać, że punkt
jest osią potęgową pary okręgów z zadania, więc wystarczy wykazać, że punkt 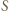 ma jednakową względem nich potęgę. Można to zrobić za pomocą podobieństwa trójkątów
ma jednakową względem nich potęgę. Można to zrobić za pomocą podobieństwa trójkątów 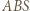 i
i 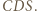
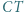 jest wysokością trójkąta
jest wysokością trójkąta 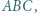 w którym
w którym 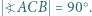 Okrąg o środku
Okrąg o środku  i promieniu
i promieniu  oraz okrąg opisany na trójkącie
oraz okrąg opisany na trójkącie  przecinają się w punktach
przecinają się w punktach 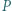 i
i 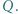 Dowieść, że prosta
Dowieść, że prosta 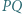 przechodzi przez środek odcinka
przechodzi przez środek odcinka 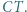
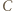 ma równą potęgę względem obu okręgów z zadania. Umiejętne zastosowanie twierdzenia Pitagorasa powinno wystarczyć.
ma równą potęgę względem obu okręgów z zadania. Umiejętne zastosowanie twierdzenia Pitagorasa powinno wystarczyć.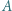 poprowadzono styczne do okręgu
poprowadzono styczne do okręgu 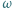 o środku
o środku 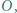 w punktach
w punktach 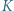 i
i 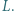 Punkt
Punkt 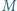 jest środkiem odcinka
jest środkiem odcinka 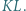 Okrąg
Okrąg 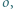 przechodzący przez punkty
przechodzący przez punkty 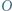 i
i 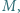 przecina okrąg
przecina okrąg 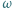 w punktach
w punktach 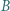 i
i 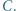 Wykazać, że punkty
Wykazać, że punkty 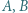 i
i 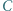 leżą na jednej prostej.
leżą na jednej prostej.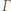 będzie okręgiem o średnicy
będzie okręgiem o średnicy 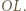 Wówczas okrąg
Wówczas okrąg 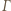 przechodzi przez punkt
przechodzi przez punkt 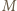 i jest styczny do prostej
i jest styczny do prostej 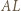 w punkcie
w punkcie 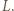 Wystarczy zauważyć, że punkt
Wystarczy zauważyć, że punkt 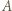 ma jednakową potęgę względem okręgów
ma jednakową potęgę względem okręgów 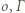 i
i 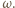
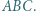 Okrąg styczny do odcinków
Okrąg styczny do odcinków 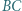 i
i 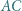 przecina odcinek
przecina odcinek 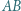 w punktach
w punktach 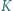 i
i 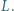 Wykazać, że
Wykazać, że 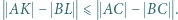
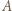 i
i 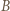 względem okręgu z zadania i odjąć stronami otrzymane równości.
względem okręgu z zadania i odjąć stronami otrzymane równości.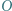 jest środkiem okręgu opisanego, a punkt
jest środkiem okręgu opisanego, a punkt 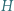 ortocentrum trójkąta ostrokątnego i różnobocznego
ortocentrum trójkąta ostrokątnego i różnobocznego 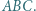 Punkty
Punkty 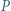 i
i 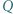 leżą odpowiednio na odcinkach
leżą odpowiednio na odcinkach 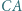 i
i 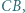 przy czym czworokąt
przy czym czworokąt 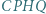 jest równoległobokiem. Wykazać, że
jest równoległobokiem. Wykazać, że 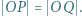
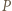 i
i 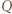 mają równą potęgę względem okręgu opisanego na trójkącie
mają równą potęgę względem okręgu opisanego na trójkącie 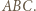 Do tego celu wystarczy podobieństwo odpowiednich trójkątów.
Do tego celu wystarczy podobieństwo odpowiednich trójkątów.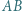 i prostopadła do niej cięciwa
i prostopadła do niej cięciwa 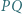 okręgu
okręgu  przecinają się w punkcie
przecinają się w punkcie 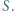 Okrąg
Okrąg 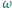 jest styczny (wewnętrznie) do okręgu
jest styczny (wewnętrznie) do okręgu  i do odcinków
i do odcinków 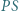 oraz
oraz 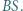 Niech
Niech 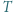 będzie punktem styczności okręgu
będzie punktem styczności okręgu 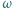 do odcinka
do odcinka 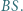 Wykazać, że
Wykazać, że 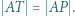
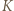 i
i 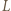 będą punktami styczności okręgu
będą punktami styczności okręgu 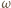 do, odpowiednio, okręgu
do, odpowiednio, okręgu  i odcinka
i odcinka 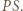 Wówczas punkty
Wówczas punkty 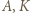 i
i 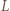 są współliniowe, gdyż punkt
są współliniowe, gdyż punkt 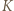 jest obrazem punktu
jest obrazem punktu 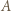 w jednokładności względem punktu
w jednokładności względem punktu 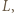 która przekształca okrąg
która przekształca okrąg  na
na 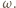 Mamy też
Mamy też 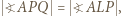 bo są to kąty wpisane, oparte na równej długości łukach okręgu
bo są to kąty wpisane, oparte na równej długości łukach okręgu  Resztę załatwia podobieństwo trójkątów i potęga punktu
Resztę załatwia podobieństwo trójkątów i potęga punktu 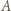 względem okręgu
względem okręgu 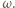
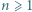 różnych okręgów dzieli płaszczyznę na co najwyżej
różnych okręgów dzieli płaszczyznę na co najwyżej 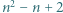 obszarów.
obszarów.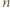 okręgów na płaszczyźnie, to po dorysowaniu jeszcze jednego liczba obszarów wzrośnie o co najwyżej
okręgów na płaszczyźnie, to po dorysowaniu jeszcze jednego liczba obszarów wzrośnie o co najwyżej 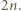
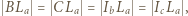 wykonując obliczenia na kątach.
wykonując obliczenia na kątach.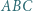 przecinają się w punkcie
przecinają się w punkcie 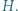 Punkt
Punkt 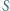 jest środkiem tego łuku
jest środkiem tego łuku 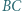 okręgu opisanego na trójkącie
okręgu opisanego na trójkącie 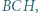 który zawiera punkt
który zawiera punkt 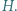 Wyznaczyć miarę kąta
Wyznaczyć miarę kąta 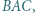 jeśli spełniona jest równość
jeśli spełniona jest równość 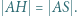
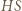 jest dwusieczną
jest dwusieczną 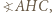 z czego można otrzymać
z czego można otrzymać 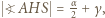 a dalej
a dalej 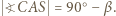 Dodatkowo punkt
Dodatkowo punkt 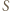 leży na symetralnej odcinka
leży na symetralnej odcinka 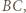 więc jest środkiem okręgu opisanego na trójkącie
więc jest środkiem okręgu opisanego na trójkącie 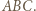
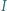 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 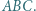 Prosta
Prosta 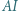 przecina odcinek
przecina odcinek 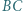 w punkcie
w punkcie 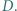 Symetralna odcinka
Symetralna odcinka 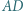 przecina proste
przecina proste 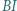 oraz
oraz 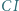 odpowiednio w punktach
odpowiednio w punktach 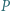 i
i 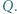 Dowieść, że wysokości trójkąta
Dowieść, że wysokości trójkąta 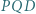 przecinają się w punkcie
przecinają się w punkcie 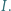
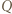 leży na okręgu opisanym na trójkącie
leży na okręgu opisanym na trójkącie 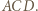 Stąd można wykazać, że
Stąd można wykazać, że 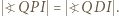
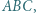 w którym
w którym 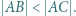 Dwusieczna kąta
Dwusieczna kąta 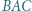 przecina bok
przecina bok 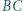 w punkcie
w punkcie 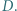 Punkt
Punkt 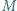 jest środkiem boku
jest środkiem boku 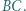 Udowodnić, że prosta przechodząca przez środki okręgów opisanych na trójkątach
Udowodnić, że prosta przechodząca przez środki okręgów opisanych na trójkątach 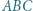 i
i 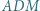 jest równoległa do prostej
jest równoległa do prostej 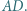
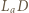 i
i 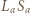 są średnicami okręgów opisanych odpowiednio na trójkątach
są średnicami okręgów opisanych odpowiednio na trójkątach 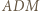 i
i 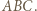
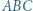 wpisano okrąg o środku
wpisano okrąg o środku 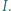 Proste
Proste 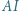 i
i 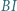 przecinają okrąg opisany na trójkącie
przecinają okrąg opisany na trójkącie 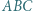 odpowiednio w punktach
odpowiednio w punktach 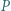 i
i 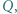 różnych od
różnych od 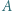 i
i 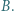 Punkt
Punkt 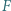 jest takim punktem, że czworokąt
jest takim punktem, że czworokąt 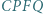 jest równoległobokiem. Dowieść, że jeśli
jest równoległobokiem. Dowieść, że jeśli 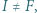 to
to 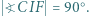
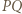 jest symetralną odcinka
jest symetralną odcinka 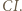 Ponadto trójkąty
Ponadto trójkąty 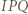 i
i 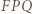 są przystające, co daje
są przystające, co daje 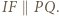
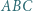 jest styczny do odcinków
jest styczny do odcinków 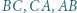 w punktach odpowiednio
w punktach odpowiednio 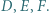 Niech
Niech 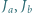 i
i 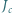 będą odpowiednio środkami okręgów wpisanych w trójkąty
będą odpowiednio środkami okręgów wpisanych w trójkąty 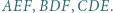 Prosta
Prosta 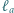 jest symetryczna do prostej
jest symetryczna do prostej 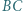 względem prostej
względem prostej 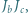 analogicznie określamy proste
analogicznie określamy proste 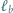 i
i 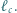 Dowieść, że proste
Dowieść, że proste 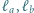 i
i 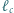 przecinają się w jednym punkcie.
przecinają się w jednym punkcie.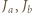 i
i 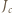 są środkami łuków
są środkami łuków 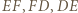 okręgu opisanego na trójkącie
okręgu opisanego na trójkącie 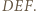 Punkt
Punkt 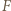 i środek
i środek 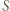 okręgu wpisanego w trójkąt
okręgu wpisanego w trójkąt 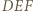 są symetryczne względem prostej
są symetryczne względem prostej 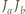 (por. poprzednie zadanie), więc
(por. poprzednie zadanie), więc 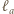 przechodzi przez punkt
przechodzi przez punkt 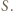
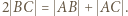 Zastosować twierdzenie Ptolemeusza dla czworokąta
Zastosować twierdzenie Ptolemeusza dla czworokąta 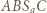 oraz twierdzenie o trójliściu, by wykazać, że punkt
oraz twierdzenie o trójliściu, by wykazać, że punkt 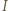 jest środkiem odcinka
jest środkiem odcinka 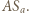
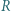 i opisany na trójkącie o promieniu
i opisany na trójkącie o promieniu 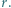 Odległość między środkami tych okręgów jest równa
Odległość między środkami tych okręgów jest równa 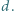 Dowieść, że
Dowieść, że 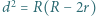 (twierdzenie Eulera).
(twierdzenie Eulera).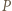 będzie rzutem prostokątnym punktu
będzie rzutem prostokątnym punktu 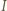 na odcinek
na odcinek 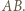 Trójkąty
Trójkąty 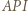 oraz
oraz 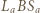 są podobne, więc
są podobne, więc 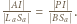 Po zastosowaniu twierdzenia o trójliściu i przekształceniach otrzymamy
Po zastosowaniu twierdzenia o trójliściu i przekształceniach otrzymamy 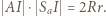 Z drugiej strony,
Z drugiej strony, 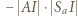 jest potęgą punktu
jest potęgą punktu 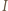 względem okręgu opisanego na trójkącie
względem okręgu opisanego na trójkącie 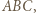 czyli wynosi
czyli wynosi 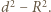
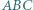 jest styczny do boków
jest styczny do boków 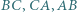 odpowiednio w punktach
odpowiednio w punktach 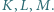 Udowodnij, że proste przechodzące przez środki odcinków
Udowodnij, że proste przechodzące przez środki odcinków 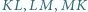 i prostopadłe odpowiednio do boków
i prostopadłe odpowiednio do boków 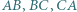 przecinają się w jednym punkcie.
przecinają się w jednym punkcie.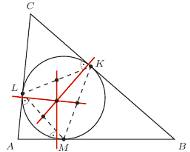
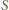 oznacza środek ciężkości trójkąta
oznacza środek ciężkości trójkąta 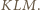 Wówczas jednokładność o środku
Wówczas jednokładność o środku 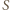 i skali -2 przeprowadza środek odcinka
i skali -2 przeprowadza środek odcinka 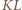 na punkt
na punkt 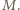 Wobec tego przy tej jednokładności obrazem prostej przechodzącej przez tenże środek i prostopadłej do
Wobec tego przy tej jednokładności obrazem prostej przechodzącej przez tenże środek i prostopadłej do 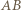 jest prosta przechodząca przez punkt
jest prosta przechodząca przez punkt 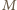 i prostopadła do
i prostopadła do 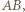 czyli prosta przechodząca przez środek
czyli prosta przechodząca przez środek 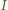 okręgu wpisanego w trójkąt
okręgu wpisanego w trójkąt 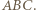 Analogicznie obrazami pozostałych opisanych w zadaniu prostych też są proste przez
Analogicznie obrazami pozostałych opisanych w zadaniu prostych też są proste przez 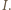 Stąd również wyjściowe proste są współpękowe.
Stąd również wyjściowe proste są współpękowe.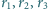 są parami styczne zewnętrznie oraz są styczne wewnętrznie do okręgu o promieniu
są parami styczne zewnętrznie oraz są styczne wewnętrznie do okręgu o promieniu 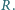 Wykazać, że
Wykazać, że
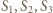 środki tych trzech okręgów, a środek dużego okręgu przez
środki tych trzech okręgów, a środek dużego okręgu przez 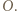 Zgodnie z warunkami zadania,
Zgodnie z warunkami zadania,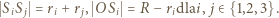
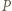 będzie środkiem ciężkości trójkąta
będzie środkiem ciężkości trójkąta 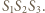 Jest to punkt minimalizujący sumę kwadratów odległości od wierzchołków (znany fakt, zresztą łatwy do wykazania). Zatem
Jest to punkt minimalizujący sumę kwadratów odległości od wierzchołków (znany fakt, zresztą łatwy do wykazania). Zatem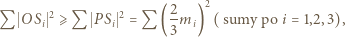
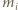 jest długością środkowej, wychodzącej z wierzchołka
jest długością środkowej, wychodzącej z wierzchołka 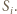 Suma kwadratów długości środkowych to
Suma kwadratów długości środkowych to 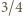 sumy kwadratów długości boków (kolejny znany wzór). Nierówność (2) pokazuje więc, że
sumy kwadratów długości boków (kolejny znany wzór). Nierówność (2) pokazuje więc, że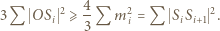
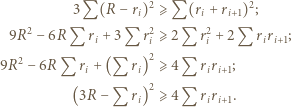
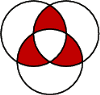
 i przechodzi przez środki obu pozostałych. Wyznacz pole kolorowego obszaru.
i przechodzi przez środki obu pozostałych. Wyznacz pole kolorowego obszaru.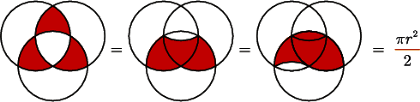


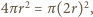 co kończy dowód.
co kończy dowód.
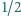 podzielono na równe części i narysowano półokręgi jak na rysunku. Wykaż, że jednobarwne obszary mają równe pola i obwody.
podzielono na równe części i narysowano półokręgi jak na rysunku. Wykaż, że jednobarwne obszary mają równe pola i obwody.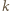 liczbę części i przez
liczbę części i przez 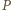 pole półkola o średnicy
pole półkola o średnicy 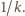 Wówczas pole półkola o średnicy
Wówczas pole półkola o średnicy 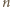 -krotnie większej równe jest
-krotnie większej równe jest 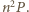 Ponadto różnica pól półkoli o średnicy
Ponadto różnica pól półkoli o średnicy 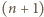 -krotnie większej i
-krotnie większej i 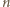 -krotnie większej wynosi
-krotnie większej wynosi 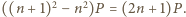
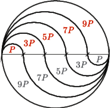
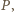 a pola jednobarwnych obszarów to kolejno
a pola jednobarwnych obszarów to kolejno 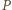 razy:
razy: 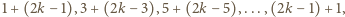 czyli zawsze
czyli zawsze 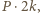 a więc istotnie wszystkie są równe.
a więc istotnie wszystkie są równe.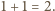 Półokrąg o średnicy
Półokrąg o średnicy 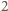 ma długość
ma długość 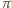 ; półokręgi o średnicach sumujących się do
; półokręgi o średnicach sumujących się do 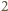 również mają taką łączną długość.
również mają taką łączną długość.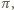 czyli obwodowi wyjściowego koła.
czyli obwodowi wyjściowego koła.