Mała Delta
Zrób to sam
Płaszczyzna hiperboliczna z papieru

Od czasów starożytnych Greków wiadomo, że jest pięć brył foremnych: czworościan, sześcian, ośmiościan, dwunastościan i dwudziestościan. W każdym wierzchołku może się spotkać 3, 4 lub 5 trójkątów, 3 czworokąty lub 3 pięciokąty. Dużo później skompletowano wielościany półforemne, jednak i tu w żadnym z nich nie pojawia się siedmiokąt. Spróbujmy dać mu szansę...

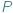 będzie wielościanem wypukłym o trójkątnych ścianach. Oznaczmy przez
będzie wielościanem wypukłym o trójkątnych ścianach. Oznaczmy przez 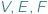 odpowiednio liczbę jego wierzchołków, krawędzi i ścian. Jakie trójki
odpowiednio liczbę jego wierzchołków, krawędzi i ścian. Jakie trójki 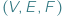 liczb naturalnych możemy w ten sposób uzyskać? Bez trudu możemy wypisać dwie równości:
liczb naturalnych możemy w ten sposób uzyskać? Bez trudu możemy wypisać dwie równości: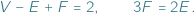
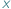 i
i 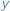 mamy
mamy 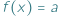 i
i 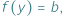 to w przedziale
to w przedziale 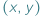 są przyjmowane wszystkie wartości między
są przyjmowane wszystkie wartości między  i
i 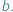 Jest to bardzo skuteczne narzędzie do rozwiązywania wielu zadań z analizy matematycznej. Okazuje się, że podobny motyw możemy zaobserwować także w zadaniach dotyczących liczb całkowitych...
Jest to bardzo skuteczne narzędzie do rozwiązywania wielu zadań z analizy matematycznej. Okazuje się, że podobny motyw możemy zaobserwować także w zadaniach dotyczących liczb całkowitych...