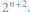Planeta obiegająca dowolną gwiazdę może przejawić swoją obecność na kilka sposobów. Jej działanie grawitacyjne powinno powodować okresowe zmiany położenia gwiazdy. Jeżeli gwiazda już się porusza, to obserwator zobaczy, że jej tor jest wężykiem. Ruch gwiazdy wzdłuż promienia widzenia przejawi się jako zmiany jej prędkości radialnej.

Wysoko, trochę ku zachodowi, widzimy w kwietniowe wieczory niepozorny gwiazdozbiór Raka...

Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty

Sieci optyczne są nowym materiałem, będącym cały czas przedmiotem aktywnych badań. W ostatnich latach bardzo szybko pojawiają się nowe możliwości eksperymentalne, rozwijana jest teoria. Można je zastosować do badania mechanizmów fizyki ciała stałego.

Dwa punkty materialne, każdy o masie  przymocowane są do przeciwległych punktów nieważkiej obręczy o promieniu  która toczy się bez tarcia po poziomej płaszczyźnie, pozostając przez cały czas prostopadła do tej płaszczyzny. Prędkość środka masy układu (punkt  na rysunku 1) wynosi  a prędkość kątowa obrotu względem osi przechodzącej przez  jest równa  Jaka jest energia tego układu?

W tym odcinku będziemy kontynuowali doświadczenia pozwalające poznać zachowanie się ciał niesztywnych w ruchu obrotowym. Skoncentrujemy się na cieczach o dużej lepkości i materiałach sypkich.

W Bajtocji można spotkać wędrownych treserów pcheł. Pchły uczone są tańca, polegającego na wykonywaniu precyzyjnych skoków w rytm muzyki. Dokładnie wygląda to tak: treser układa na stole w rządku ponumerowane kolejno żetony. Na każdym żetonie, oprócz jego numeru, jest również napisany numer żetonu, na który powinna z niego skoczyć pchła – na każdym żetonie ten numer jest inny. Następnie treser ustawia po jednej pchle na każdym z żetonów i włącza muzykę. Na początku każdego taktu każda z pcheł wykonuje skok wprost na żeton, którego numer jest napisany na żetonie, na którym w danej chwili stoi.

W naszym zespole badawczym analizujemy wiele różnych zagadnień, które występują w różnych aspektach. Nic w tym dziwnego, wszak algorytmika jest bardzo szeroką dziedziną. Zdarza się i tak, że to samo zagadnienie pojawia się w wielu kontekstach. Taka sytuacja ma miejsce w przypadku problemu drzewa Steinera.

W tym kąciku spróbujemy rozwiązać zadanie Electric needs pochodzące z drużynowych zawodów studenckich z serii ACM ICPC, a konkretnie z mistrzostw Ameryki Łacińskiej 2010.

Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty

Prosta operacja symetryzacji pozwala w elementarny sposób rozwiązywać nieelementarne problemy...

Tematem mojej pracy były własności pewnych szczególnych punktów na płaszczyźnie – punktów tytułowego zbioru W poniższym tekście przedstawię niektóre z tych własności oraz przykłady pokazujące, że przy użyciu dowiedzionych twierdzeń można wyciągnąć wiele niemal natychmiastowych wniosków.

W dniu 8 stycznia 2011 roku odbyły się zawody II stopnia VI Olimpiady Matematycznej Gimnazjalistów, w których uczestniczyło 669 uczniów. Spośród nich 187 zostało zakwalifikowanych do zawodów stopnia III.

Na pierwszym etapie tegorocznej Olimpiady Matematycznej pojawiło się poniższe zadanie 1 o numerowaniu krawędzi dwunastościanu. Spośród licznych zadań o podobnej tematyce prezentujemy kilka o dość różnorodnych rozwiązaniach.

Jak wiadomo, każdy człowiek ma dwoje rodziców. Skoro każdy z rodziców też jest człowiekiem, ta rekurencyjna zależność pozwala w prosty sposób wyznaczyć liczbę przodków dowolnej osoby w linii prostej w kolejnych pokoleniach: czworo babć i dziadków, ośmioro prababć i pradziadków, a zatem ogólnie  dziadków obojga płci mamy

Tem może niezbyt elegancki, tytuł nasunął mi artykuł w naukowym tygodniku Nature o rozszyfrowaniu genomu orangutana. Wraz z szympansem i gorylem tworzą grupę małp człekokształtnych, a ich genomy porównuje się z genomem człowieka.

Pełnia księżyca pełni zauważalną rolę w naszej kulturze. Na fazach księżyca oparte są najstarsze materialnie udokumentowane sposoby zliczania dni, a siódemka jest w większości cywilizacji jakoś wyróżniona. Liczba dni tygodnia jest najlepszym, ale nie jedynym przykładem.