Czworościan i kule»Zadanie
o zadaniu...
- Zadanie olimpijskie: VI olimpiada Matematyczna (II stopień)
- Zadanie pochodzi z artykułu Czworościan i kule
- Publikacja w Delcie: kwiecień 2011
- Publikacja elektroniczna: 31-03-2011
Dany jest czworościan foremny opisany na sferze o promieniu
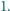 Udowodnij, że w tym czworościanie można umieścić 6 kul o promieniu
Udowodnij, że w tym czworościanie można umieścić 6 kul o promieniu
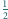 w taki sposób, aby każde dwie kule miały co najwyżej jeden punkt
wspólny.
w taki sposób, aby każde dwie kule miały co najwyżej jeden punkt
wspólny.

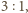 licząc od wierzchołka. Punkt ten jest jednocześnie środkiem kuli wpisanej i
opisanej na czworościanie foremnym.
licząc od wierzchołka. Punkt ten jest jednocześnie środkiem kuli wpisanej i
opisanej na czworościanie foremnym.
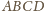 można wpisać kulę
można wpisać kulę
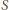 o środku
o środku
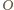 i promieniu 1, wysokość tego czworościanu wynosi 4
(na podstawie przytoczonej własności). Przekształćmy czworościan
foremny
i promieniu 1, wysokość tego czworościanu wynosi 4
(na podstawie przytoczonej własności). Przekształćmy czworościan
foremny
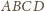 przez jednokładność względem punktu
przez jednokładność względem punktu
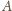 o skali
o skali
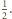 W efekcie otrzymamy czworościan
W efekcie otrzymamy czworościan
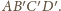 Korzystając z własności jednokładności, wnioskujemy, że płaszczyzna
Korzystając z własności jednokładności, wnioskujemy, że płaszczyzna
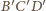 przecina wysokość
przecina wysokość
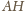 w punkcie
w punkcie
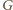 w taki
sposób, że
w taki
sposób, że
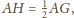 a kula
a kula
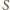 jest również styczna do
płaszczyzny
jest również styczna do
płaszczyzny
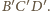 Zatem kula
Zatem kula
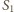 wpisana w czworościan
wpisana w czworościan
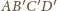 ma promień
ma promień
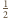 i ma tylko jeden punkt wspólny z kulą
i ma tylko jeden punkt wspólny z kulą
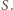
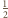 umieszczone w każdym „rogu” czworościanu
umieszczone w każdym „rogu” czworościanu
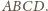 Każda z tych kul
ma tylko jeden punkt wspólny z kulą
Każda z tych kul
ma tylko jeden punkt wspólny z kulą
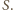 Ponieważ kula
Ponieważ kula
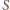 ma
promień 1, więc można umieścić w niej dwie kule o promieniu
ma
promień 1, więc można umieścić w niej dwie kule o promieniu
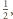 które mają tylko jeden punkt wspólny.
które mają tylko jeden punkt wspólny.
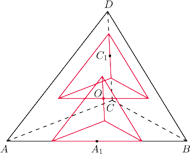
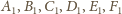 będą odpowiednio środkami krawędzi
będą odpowiednio środkami krawędzi
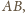
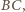
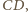
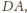
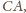
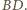 Przekształćmy kulę
Przekształćmy kulę
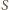 i czworościan
i czworościan
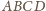 przez
przez 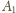 i skali
i skali
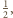
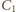 i skali
i skali
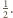
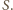 Zatem kule wpisane w te
czworościany nie mają punktów wspólnych.
Zatem kule wpisane w te
czworościany nie mają punktów wspólnych.
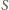 przez
przez 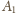 i skali
i skali
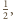
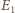 i skali
i skali
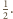
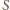 będą środki kul o promieniach
będą środki kul o promieniach
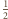 znajdujące się w połowie odcinków
znajdujące się w połowie odcinków
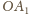 i
i
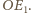 Wykażemy teraz,
że kule te nie mają punktów wspólnych.
Wykażemy teraz,
że kule te nie mają punktów wspólnych.
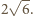 Zatem odległość
punktów
Zatem odległość
punktów
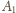 i
i
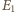 wynosi
wynosi
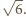 Środki boków
Środki boków
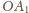 i
i
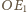 w trójkącie
w trójkącie
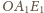 pozostają w odległości
pozostają w odległości
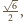 która
jest większa od 1.
która
jest większa od 1.
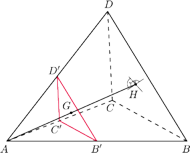
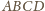 można umieścić sześć
kul: każda z nich jest obrazem kuli wpisanej w czworościan
można umieścić sześć
kul: każda z nich jest obrazem kuli wpisanej w czworościan
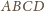 w
jednokładności o skali
w
jednokładności o skali
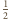 i środku będącym środkiem krawędzi
czworościanu.
i środku będącym środkiem krawędzi
czworościanu.