Klub 44M - zadania IV 2011»Zadanie 620
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania IV 2011
- Publikacja w Delcie: kwiecień 2011
- Publikacja elektroniczna: 31 marca 2011
- Artykuł źródłowy w wersji do druku [application/pdf]: (157 KB)
Zadanie zaproponował pan Witold Bednarek z Łodzi.
Niech
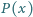 będzie wielomianem stopnia dodatniego o współczynnikach
całkowitych. Wykazać, że dla każdej liczby naturalnej
będzie wielomianem stopnia dodatniego o współczynnikach
całkowitych. Wykazać, że dla każdej liczby naturalnej
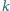 istnieje taka
liczba całkowita
istnieje taka
liczba całkowita
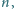 że liczba
że liczba
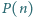 ma co najmniej
ma co najmniej
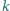 różnych dzielników pierwszych.
różnych dzielników pierwszych.

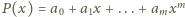 (
(
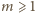 ).
).
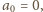 wystarczy wziąć dowolną liczbę
wystarczy wziąć dowolną liczbę
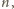 będącą iloczynem
będącą iloczynem
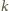 różnych liczb pierwszych. Są one oczywiście dzielnikami liczby
różnych liczb pierwszych. Są one oczywiście dzielnikami liczby
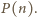 Dalej przyjmijmy, że
Dalej przyjmijmy, że
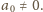
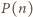 jest nieskończony. Przypuśćmy bowiem, że jest to zbiór
skończony
jest nieskończony. Przypuśćmy bowiem, że jest to zbiór
skończony
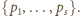 Biorąc jako
Biorąc jako
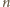 dowolną liczbę postaci
dowolną liczbę postaci
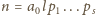 (
(
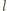 całkowite), mamy
całkowite), mamy
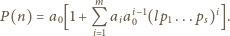
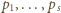 (a swoboda wyboru
(a swoboda wyboru
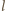 pozwala przyjąć, że jest różna
od
pozwala przyjąć, że jest różna
od
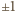 ); ma więc jakiś inny dzielnik pierwszy, wbrew uczynionemu
przypuszczeniu.
); ma więc jakiś inny dzielnik pierwszy, wbrew uczynionemu
przypuszczeniu.
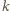 istnieją różne liczby pierwsze
istnieją różne liczby pierwsze
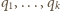 oraz takie liczby całkowite
oraz takie liczby całkowite
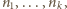 że
że
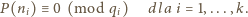
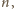 spełniającą układ kongruencji
spełniającą układ kongruencji

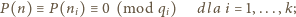
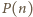 ma więc co najmniej
ma więc co najmniej
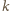 różnych dzielników
pierwszych.
różnych dzielników
pierwszych.