Klub 44M - zadania IV 2011»Zadanie 619
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania IV 2011
- Publikacja w Delcie: kwiecień 2011
- Publikacja elektroniczna: 31 marca 2011
- Artykuł źródłowy w wersji do druku [application/pdf]: (157 KB)
Szachownica o rozmiarach
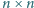 została pokryta płytkami
została pokryta płytkami
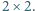 Każda płytka pokrywa dokładnie cztery pola. Płytki zachodzą na siebie, ale nie
wystają poza brzeg szachownicy. Liczba płytek przekracza
Każda płytka pokrywa dokładnie cztery pola. Płytki zachodzą na siebie, ale nie
wystają poza brzeg szachownicy. Liczba płytek przekracza
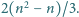 Dowieść, że można usunąć jedną płytkę tak, by pozostałe płytki nadal
pokrywały całą szachownicę.
Dowieść, że można usunąć jedną płytkę tak, by pozostałe płytki nadal
pokrywały całą szachownicę.

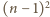 punktów kratowych (w każdym
spotykają się cztery pola szachownicy). Wyróżnijmy te punkty kratowe, na
które padły środki płytek. Punkty kratowe leżą w
punktów kratowych (w każdym
spotykają się cztery pola szachownicy). Wyróżnijmy te punkty kratowe, na
które padły środki płytek. Punkty kratowe leżą w
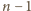 rzędach po
rzędach po
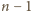 punktów; liczba punktów wyróżnionych przekracza
punktów; liczba punktów wyróżnionych przekracza
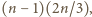 więc w pewnym rzędzie jest ich więcej niż
więc w pewnym rzędzie jest ich więcej niż
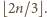
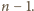 Wystarczy
wykazać, że pewna trójka
Wystarczy
wykazać, że pewna trójka
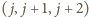 składa się z punktów
wyróżnionych; można wtedy bezkarnie usunąć płytkę o środku w punkcie
składa się z punktów
wyróżnionych; można wtedy bezkarnie usunąć płytkę o środku w punkcie
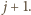
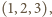
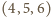 itd.
jest punkt niewyróżniony. Jest
itd.
jest punkt niewyróżniony. Jest
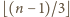 trójek postaci
trójek postaci
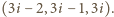 W takim razie liczba punktów wyróżnionych
(w rozważanym rzędzie) nie przekracza różnicy
W takim razie liczba punktów wyróżnionych
(w rozważanym rzędzie) nie przekracza różnicy
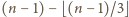 ;
zaś ta różnica równa się
;
zaś ta różnica równa się
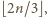 o czym można się przekonać,
rozpatrując trzy możliwe reszty z dzielenia
o czym można się przekonać,
rozpatrując trzy możliwe reszty z dzielenia
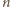 przez 3. Sprzeczność –
wyróżnionych punktów miało być w tym rzędzie więcej.
przez 3. Sprzeczność –
wyróżnionych punktów miało być w tym rzędzie więcej.