W sieci Bayesa
Rozpoczniemy od żartobliwej, acz pouczającej historyjki: podczas rozmowy dwóch stałych bywalców lokalnego baru jeden z nich mówi do drugiego "Noszenie kaloszy jest bardzo niezdrowe; ilekroć budzę się rano i mam je na nogach, boli mnie głowa"...
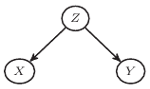
Rys. 1

Łatwo wskazać lukę w przedstawionym rozumowaniu (psując odrobinę dowcip, ale czegóż nie robi się dla dobra nauki): choć niewątpliwie spędzenie nocy w kaloszach i poranny ból głowy często występowały wspólnie, nie można na tej podstawie powiedzieć, że to pierwsze jest przyczyną drugiego. Oba mają po prostu wspólną praprzyczynę, jaką jest niechlubne zamiłowanie autora uwagi do wysokoprocentowych trunków. Zależność tę można przedstawić graficznie, tak jak na rysunku 1, na którym 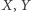 i
i 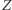 związane są odpowiednio z kaloszami na nogach, porannym bólem głowy i przesadną konsumpcją poprzedniego wieczora. Zwróćmy uwagę, że (1) nie każdy wieczór spędzony jest w barze (na szczęście), (2) nie każdy wieczór spędzony w barze skutkuje bolącą głową (kaloszami na nogach) następnego ranka i (3) nie zawsze boląca głowa (kalosze) są dowodem na wieczór spędzony w barze. Sugeruje to, aby na
związane są odpowiednio z kaloszami na nogach, porannym bólem głowy i przesadną konsumpcją poprzedniego wieczora. Zwróćmy uwagę, że (1) nie każdy wieczór spędzony jest w barze (na szczęście), (2) nie każdy wieczór spędzony w barze skutkuje bolącą głową (kaloszami na nogach) następnego ranka i (3) nie zawsze boląca głowa (kalosze) są dowodem na wieczór spędzony w barze. Sugeruje to, aby na  patrzeć jak na zmienne losowe, które określone wartości (powiedzmy 0 i 1) przyjmują z określonym prawdopodobieństwem. Jest zatem sensowne pytanie na przykład o prawdopodobieństwo obudzenia się z kaloszami na nogach bez bólu głowy oraz gdy nie byliśmy poprzedniego dnia w barze, czyli
patrzeć jak na zmienne losowe, które określone wartości (powiedzmy 0 i 1) przyjmują z określonym prawdopodobieństwem. Jest zatem sensowne pytanie na przykład o prawdopodobieństwo obudzenia się z kaloszami na nogach bez bólu głowy oraz gdy nie byliśmy poprzedniego dnia w barze, czyli
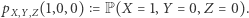 |
Funkcja 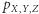 ma kilka funkcji "pochodnych", można z niej, na przykład, odczytać prawdopodobieństwo obudzenia się z kaloszami
ma kilka funkcji "pochodnych", można z niej, na przykład, odczytać prawdopodobieństwo obudzenia się z kaloszami
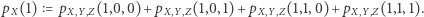 |
Podobnie możemy zdefiniować 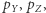 a także
a także 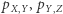 i
i 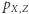 - za każdym razem sumujemy
- za każdym razem sumujemy 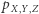 dla wszystkich możliwych wartości zmiennych, które nie występują w dolnym indeksie (otrzymujemy w ten sposób rozkłady brzegowe). Jesteśmy też w stanie obliczyć prawdopodobieństwo obudzenia się bez kaloszy pod warunkiem spędzenia wieczoru w barze, czyli
dla wszystkich możliwych wartości zmiennych, które nie występują w dolnym indeksie (otrzymujemy w ten sposób rozkłady brzegowe). Jesteśmy też w stanie obliczyć prawdopodobieństwo obudzenia się bez kaloszy pod warunkiem spędzenia wieczoru w barze, czyli
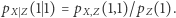 |
Analogicznie możemy określić funkcje 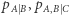 czy
czy 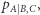 gdzie pod
gdzie pod 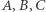 można dowolnie wstawić
można dowolnie wstawić 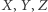 ; otrzymamy w ten sposób rozkłady warunkowe. Zwróćmy uwagę na oczywistą algebraicznie równość
; otrzymamy w ten sposób rozkłady warunkowe. Zwróćmy uwagę na oczywistą algebraicznie równość
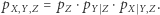 |
(1) |
Wspomniany na początku bywalec baru zaobserwował zależność między kaloszami i bólem głowy, możemy jednak podejrzewać, że zjawiska te są niezależne pod warunkiem pobytu w barze. Oznacza to, że jeśli dysponujemy informacją o sposobie spędzenia poprzedniego wieczoru, to wiedza o kaloszach na nogach o poranku nie wpłynie na naszą ocenę szansy na ból głowy. Wykorzystując wprowadzone przez nas oznaczenia, możemy to zapisać na trzy algebraicznie równoważne sposoby
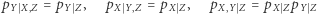 |
(wszystkie te równości można szybko sprowadzić do 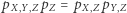 ). Równość (1) możemy wówczas zapisać jako
). Równość (1) możemy wówczas zapisać jako
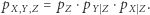 |
(2) |
W takiej sytuacji mówimy, że funkcja 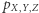 faktoryzuje się względem grafu przedstawionego na rysunku 1 - przedstawia się bowiem jako iloczyn, w którym każdy czynnik jest postaci
faktoryzuje się względem grafu przedstawionego na rysunku 1 - przedstawia się bowiem jako iloczyn, w którym każdy czynnik jest postaci 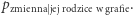 Jeśli w każdym z czynników ze zmiennych, po których warunkujemy, nie da się niczego uszczknąć (tak, jak przechodząc z zawsze prawdziwego (1) do szczególnego (2)), to mówimy, że dany graf jest siecią bayesowską dla funkcji
Jeśli w każdym z czynników ze zmiennych, po których warunkujemy, nie da się niczego uszczknąć (tak, jak przechodząc z zawsze prawdziwego (1) do szczególnego (2)), to mówimy, że dany graf jest siecią bayesowską dla funkcji 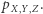 Jeśli graf z rysunku 1 jest siecią bayesowską dla naszych zmiennych, to połączenie (1) (zawsze prawdziwe!) i (2) (założenie o faktoryzacji) daje nam
Jeśli graf z rysunku 1 jest siecią bayesowską dla naszych zmiennych, to połączenie (1) (zawsze prawdziwe!) i (2) (założenie o faktoryzacji) daje nam 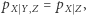 czyli warunkową niezależność
czyli warunkową niezależność 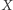 i
i 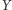 (oznaczaną jako
(oznaczaną jako 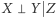 ). Z drugiej strony mamy
). Z drugiej strony mamy
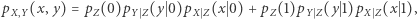 |
czego bez dodatkowych założeń nie moglibyśmy zapisać jako iloczynu dwóch funkcji, z których jedna jest zależna tylko od 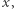 a druga tylko od
a druga tylko od 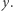 W ogólności nie występuje zatem niezależność
W ogólności nie występuje zatem niezależność 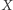 od
od 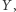 co zostało zaobserwowane przez bywalca baru.
co zostało zaobserwowane przez bywalca baru.

Rys. 2
Zastanówmy się, jakie jeszcze dwukrawędziowe sieci bayesowskie mogą rządzić zachowaniem trzech zmiennych. Gdyby 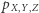 faktoryzowało się wedle grafu na rysunku 2, mielibyśmy
faktoryzowało się wedle grafu na rysunku 2, mielibyśmy 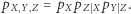 Odpowiadałoby to sytuacji, w której
Odpowiadałoby to sytuacji, w której 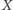 jest oceną ze sprawdzianu z trygonometrii,
jest oceną ze sprawdzianu z trygonometrii, 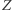 oceną roczną z matematyki, a
oceną roczną z matematyki, a 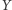 - średnią na świadectwie. Wówczas
- średnią na świadectwie. Wówczas 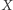 i
i 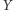 są zależne (choć delikatnie), przestaje to jednak mieć miejsce, jeśli rozpatrzymy sytuację pod warunkiem oceny z matematyki (nie mylić z warunkiem z matematyki). Odpowiada to prostej do sprawdzenia (wykorzystując
są zależne (choć delikatnie), przestaje to jednak mieć miejsce, jeśli rozpatrzymy sytuację pod warunkiem oceny z matematyki (nie mylić z warunkiem z matematyki). Odpowiada to prostej do sprawdzenia (wykorzystując 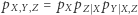 ) równości
) równości 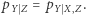
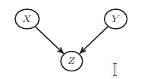
Rys. 3
Ostatnia możliwość jest przedstawiona na rysunku 3 Wówczas ma miejsce zależność 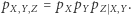 Zmienne
Zmienne 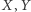 są niezależne (zachodzi bowiem
są niezależne (zachodzi bowiem 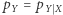 ), zależność ta nie występuje jednak w ogólności po "zwarunkowaniu" po
), zależność ta nie występuje jednak w ogólności po "zwarunkowaniu" po 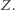 Ta sieć znajduje odzwierciedlenie w sytuacji, gdy
Ta sieć znajduje odzwierciedlenie w sytuacji, gdy 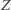 oznacza uruchomienie się alarmu przeciwpożarowego,
oznacza uruchomienie się alarmu przeciwpożarowego, 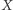 - ćwiczenia ewakuacji, a
- ćwiczenia ewakuacji, a 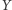 - faktyczny pożar. Nie ma powodów, aby sądzić, że szansa na wystąpienie pożaru budynku była zależna od planu przeprowadzania w nim ćwiczeń przeciwpożarowych, jeśli jednak słyszymy alarm i wiemy, że na dany dzień nie były zapowiadane ćwiczenia, powinniśmy jak najszybciej (ale bez paniki!) wziąć nogi za pas.
- faktyczny pożar. Nie ma powodów, aby sądzić, że szansa na wystąpienie pożaru budynku była zależna od planu przeprowadzania w nim ćwiczeń przeciwpożarowych, jeśli jednak słyszymy alarm i wiemy, że na dany dzień nie były zapowiadane ćwiczenia, powinniśmy jak najszybciej (ale bez paniki!) wziąć nogi za pas.
Grafy przedstawione na rysunkach 1, 2, 3 zwykło się nazywać w specjalistycznym żargonie odpowiednio "widelcem" (fork), "łańcuchem" (chain) i "zderzaczem" (collider).
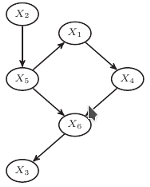
Rys. 4
Z powyższych rozważań wynika, że znajomość sieci bayesowskiej odpowiadającej funkcji 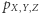 pozwala na sformułowanie wniosków o (warunkowej) niezależności. Oczywiście, rozpatrywaliśmy trywialny przypadek trzech zmiennych - co się dzieje, kiedy jest ich więcej? Kandydat na sieć bayesowską dla zmiennych
pozwala na sformułowanie wniosków o (warunkowej) niezależności. Oczywiście, rozpatrywaliśmy trywialny przypadek trzech zmiennych - co się dzieje, kiedy jest ich więcej? Kandydat na sieć bayesowską dla zmiennych 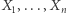 musi być grafem skierowanym, i to nie byle jakim: wymagamy od niego, aby nie miał żadnych cykli (Directed Acyclic Graph, czyli DAG). Dla przykładu, DAG przedstawiony na rysunku 4 jest siecią bayesowską dla funkcji prawdopodobieństwa
musi być grafem skierowanym, i to nie byle jakim: wymagamy od niego, aby nie miał żadnych cykli (Directed Acyclic Graph, czyli DAG). Dla przykładu, DAG przedstawiony na rysunku 4 jest siecią bayesowską dla funkcji prawdopodobieństwa 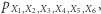 jeśli zachodzi
jeśli zachodzi
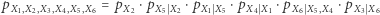 |
i nie można usunąć z powyższego napisu żadnej ze zmiennych "warunkowych". Jakie (warunkowe) niezależności spełniają wówczas zmienne 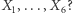 Okazuje się (i jest to jedno z podstawowych twierdzeń teorii sieci bayesowskich; jego dowód jest bardziej skomplikowany, niż może się na pierwszy rzut oka wydawać), że (warunkowa) niezależność wynika wówczas z występujących w sieci bayesowskiej
Okazuje się (i jest to jedno z podstawowych twierdzeń teorii sieci bayesowskich; jego dowód jest bardziej skomplikowany, niż może się na pierwszy rzut oka wydawać), że (warunkowa) niezależność wynika wówczas z występujących w sieci bayesowskiej 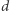 -rozdzielności. Mówimy, że wierzchołki
-rozdzielności. Mówimy, że wierzchołki 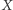 i
i 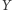 w grafie
w grafie 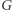 są
są 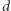 -połączone przez zbiór wierzchołków
-połączone przez zbiór wierzchołków 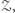 jeśli istnieje pomiędzy nimi ścieżka
jeśli istnieje pomiędzy nimi ścieżka 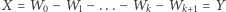 (nie bierzemy pod uwagę kierunku krawędzi) taka, że dla dowolnego
(nie bierzemy pod uwagę kierunku krawędzi) taka, że dla dowolnego 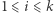 zachodzi
zachodzi
- jeśli
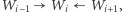 to
to 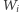 lub któryś z jego potomków (dzieci, wnuków, prawnuków…) należy do
lub któryś z jego potomków (dzieci, wnuków, prawnuków…) należy do 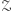
- w przeciwnym przypadku
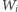 nie należy do
nie należy do 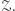
Jeśli 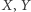 nie są
nie są 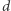 -połączone przez
-połączone przez 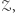 to mówimy, że są przez
to mówimy, że są przez 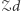 -rozdzielone. W sieci przedstawionej na rysunku 4 wierzchołki
-rozdzielone. W sieci przedstawionej na rysunku 4 wierzchołki 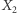 i
i 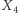 są
są 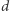 -rozdzielone przez
-rozdzielone przez 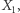 nie są jednak
nie są jednak 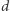 -rozdzielone przez
-rozdzielone przez 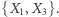 Zgodnie ze wspomnianym twierdzeniem oznacza to, że w tej sytuacji, jeśli znamy wartość
Zgodnie ze wspomnianym twierdzeniem oznacza to, że w tej sytuacji, jeśli znamy wartość 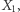 to wiedza o
to wiedza o 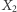 nie dostarcza nam informacji o
nie dostarcza nam informacji o 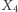 ; byłoby jednak inaczej, gdybyśmy na początku poznali jeszcze
; byłoby jednak inaczej, gdybyśmy na początku poznali jeszcze 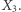 Odpowiada to "przepływowi informacji" w sieci: między
Odpowiada to "przepływowi informacji" w sieci: między 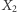 a
a 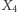 są dwie ścieżki:
są dwie ścieżki: 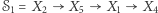 oraz
oraz 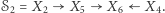 Informacja nie przepływa przez
Informacja nie przepływa przez 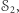 przepływa jednak przez
przepływa jednak przez 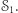 Zmieni się to, kiedy dowiemy się czegoś o
Zmieni się to, kiedy dowiemy się czegoś o 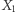 - wówczas obie ścieżki są zablokowane. Gdy jednak uzyskamy również informację na temat
- wówczas obie ścieżki są zablokowane. Gdy jednak uzyskamy również informację na temat 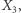 to dowiemy się czegoś o
to dowiemy się czegoś o 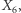 przez co "odblokujemy" ścieżkę
przez co "odblokujemy" ścieżkę 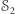 (na tej samej zasadzie, jak w przykładzie o alarmie przeciwpożarowym).
(na tej samej zasadzie, jak w przykładzie o alarmie przeciwpożarowym).

Należy podkreślić, że choć z sieci bayesowskiej możemy odczytać występujące między zmiennymi warunkowe niezależności, nie możemy na jej podstawie wnioskować o ich braku. Przykładem może być sytuacja, w której 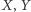 to wyniki dwóch niezależnych rzutów symetryczną monetą (gdzie orzeł kodowany jest przez 0, a reszka przez 1), natomiast
to wyniki dwóch niezależnych rzutów symetryczną monetą (gdzie orzeł kodowany jest przez 0, a reszka przez 1), natomiast 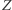 to odpowiedź na pytanie o równość
to odpowiedź na pytanie o równość 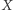 i
i 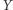 (0 - fałsz, 1 - prawda). Sieć bayesowska odpowiadająca tym zmiennym była przedstawiona na rysunku 3 Pomimo tego, że wierzchołki
(0 - fałsz, 1 - prawda). Sieć bayesowska odpowiadająca tym zmiennym była przedstawiona na rysunku 3 Pomimo tego, że wierzchołki 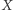 i
i 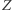 są
są 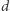 -połączone, są one niezależne. Wedle tej zasady działa każdy godny szacunku kryminał: pojedyncza wskazówka nic nie mówi o przestępcy, ale uwzględnienie ich wszystkich pozwala na doprowadzenie go przed oblicze sprawiedliwości.
-połączone, są one niezależne. Wedle tej zasady działa każdy godny szacunku kryminał: pojedyncza wskazówka nic nie mówi o przestępcy, ale uwzględnienie ich wszystkich pozwala na doprowadzenie go przed oblicze sprawiedliwości.
Czytelnik Pragmatyczny zapewne zaczął się już niecierpliwić - wprowadziliśmy mnóstwo nowych pojęć, a sformułowaliśmy tylko jedno twierdzenie, którego nawet nie udowodniliśmy; po co więc cały ten ambaras? Otóż sieci bayesowskie są bardzo poręcznym matematycznym wynalazkiem, pozwalającym w czytelny sposób przedstawiać zależności między zmiennymi losowymi. Są one użyteczne zwłaszcza wtedy, gdy chcemy zilustrować bezpośrednie związki między nimi. Działa to również w drugą stronę - choć na podstawie samych obserwacji nigdy nie jesteśmy w stanie zidentyfikować związków przyczynowo-skutkowych (jest to zasada, którą każda osoba przeprowadzająca analizę statystyczną powinna mieć na uwadze), zidentyfikowanie najprostszej sieci bayesowskiej można traktować jako krok w dobrym kierunku. Zauważmy bowiem, na przykład, że jeśli wśród zmiennych 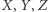 zaobserwujemy niezależność
zaobserwujemy niezależność 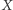 od
od 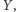 jednak zmienne te są zależne pod warunkiem
jednak zmienne te są zależne pod warunkiem 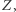 to wiemy, że mamy wówczas do czynienia ze "zderzaczem". Stanowi to pewną mglistą przesłankę (nie zawsze słuszną), że
to wiemy, że mamy wówczas do czynienia ze "zderzaczem". Stanowi to pewną mglistą przesłankę (nie zawsze słuszną), że 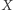 i
i 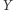 "składają się" na
"składają się" na 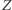 ; wiemy jednak z całą pewnością, że
; wiemy jednak z całą pewnością, że 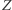 nie może być przyczyną ani
nie może być przyczyną ani 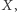 ani
ani 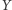 (wówczas bowiem mielibyśmy do czynienia z inną strukturą niezależności). Sprawę często komplikują tutaj tak zwane "ukryte zmienne" - jak, na przykład, wizyta w barze ostatniej nocy, która nie została uwzględniona podczas analizy...
(wówczas bowiem mielibyśmy do czynienia z inną strukturą niezależności). Sprawę często komplikują tutaj tak zwane "ukryte zmienne" - jak, na przykład, wizyta w barze ostatniej nocy, która nie została uwzględniona podczas analizy...