Rzuć monetą...

Doświadczenie, polegające na wielokrotnym rzucaniu monetą (symetryczną lub nie) ma tę zaletę, że każdy ma jakieś wyobrażenia dotyczące wyników. Nietrudno na przykład uwierzyć, że stosunek liczby orłów 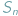$Sn$ do liczby rzutów $|n$ nie będzie się wiele różnił od $p$ - prawdopodobieństwa otrzymania orła w pojedynczym rzucie.

I rzeczywiście, jest to prawo wielkich liczb udowodnione przez Jacoba Bernoulliego pod koniec XVII w. Dokładniej, dla każdego 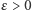$ε > 0$ mamy

lim P ( Sn− p ⩽ε) = 1. n ∞ n

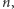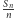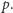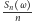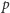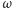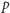Oznacza to, że im większe $|n,$ tym (na ogół) mniejsza szansa dużego odchylenia $Snn$ od $p.$ Nie znaczy to jednak, że ciąg liczb $S ω |nn---$ zmierza do $|p$ dla prawie wszystkich zdarzeń elementarnych $ω$ (czyli że $|Sn n$ dąży do $| p$ z prawdopodobieństwem 1). Gwarantuje to dopiero poniższe - mocniejsze - twierdzenie: dla każdego 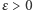$|ε> 0$ mamy

lim P (p− ε ⩽ Sn-⩽p + ε dla wszystkichn ⩾ m) = 1. m n

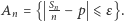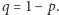Dla dowodu oszacujemy prawdopodobieństwo zdarzenia $| Sn An = { n −p ⩽ ε} .$ Niech $|q = 1− p.$ Zdarzenie 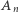$An$ przedstawimy w postaci sumy zdarzeń 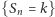${Sn = k}$ dla odpowiednio dobranych 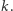$k.$ Pamiętając, że $P (Sn = k) = (nk)pkqn−k,$ otrzymamy wtedy

$pict$

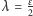W trzeciej od końca nierówności skorzystaliśmy z faktu, że $|ex⩽ 1+ x ⩽ex2 + x.$ Wybieramy teraz $|λ$ minimalizujące prawą stronę, czyli $|λ= ε 2$ i otrzymujemy nierówność Bernsteina:

$Sn −n$ 0. " class="math-display"/>

Analogicznie 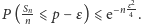$2 |P ( Snn-⩽ p− ε) ⩽ e−n$

Ponieważ dopełnienie iloczynu zbiorów jest sumą dopełnień (wzory de Morgana), więc

∞ ∞ c P( n mAn) = 1− P( n mAn)

( $Ac$ oznacza tu zdarzenie przeciwne do $|A$ ). Ponadto,

$∞ c ∞ c ∞ −n$

Stąd otrzymujemy żądany wynik.

Z powyższych rozważań wynika, że zmienna losowa 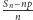$Sn−np --n--$ jest dla dużych 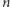$n$ silnie skupiona wokół zera. A jeśli będziemy rozpatrywać 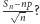$|Sn−- np? n$ O zachowaniu się tego wyrażenia mówi twierdzenie de Moivre'a-Laplace'a (de Moivre, 1733; Laplace udowodnił to twierdzenie pó@zniej, nie powołując się na poprzednika):

b Sn−-np- --1-- − x2- P (a < √ npq- < b) √ 2π-q e 2 dx, a

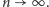gdy $n ∞ .$ Innymi słowy, 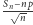$|Sn-−np- n$ ma asymptotycznie rozkład normalny (gaussowski).

Załóżmy teraz, że moneta jest symetryczna, czyli 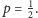$| 1 p = 2.$ Czy różnica między liczbą orłów i reszek będzie ograniczona? Posługując się, na przykład, twierdzeniem de Moivre'a-Laplace'a można udowodnić, że z prawdopodobieństwem 1 tak nie będzie. Mało tego, wartość bezwzględna różnicy jest w pewnym sensie rzędu 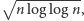$√ ---------- | nloglog n,$ a dokładniej, jeśli 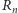$|Rn$ oznacza liczbę reszek, to

limsup √-Sn-−-Rn----= 1 n ∞ 2nlog log n

z prawdopodobieństwem 1. Oczywiście ze względu na symetrię

liminf √--Sn-−-Rn--- =− 1. n ∞ 2n loglogn

Jest to tzw. prawo iterowanego logarytmu (Chinczyn, 1924).

Wobec tego $|Sn− Rn$ będzie powracać do zera nieskończenie wiele razy z prawdopodobieństwem 1. Jednak średni czas oczekiwania na powrót do zera jest nieskończony.

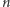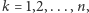I na zakończenie dość paradoksalny wynik: jeśli rzucamy symetryczną monetą $|n$ razy i zapisujemy kolejne wartości $|S − R k k$ dla $k = 1,2,...,n,$ czyli przewagę orłów nad reszkami, to okazuje się, że jest mała szansa na to, by dodatnie i ujemne różnice pojawiły się z grubsza tyle samo razy. Przeciwnie, typowy wynik to taki, że orły (lub reszki) prowadzą przez większość czasu. Można wyliczyć asymptotyczny rozkład dla czasu prowadzenia (prawo arcusa sinusa, P. Lévy, 1939): niech 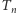$Tn$ oznacza czas, przez jaki prowadzi orzeł w serii $|n$ rzutów. Wtedy

t √ - Tn 1 2arcsin t nli m∞ P ( n-< t) = q -√--------dt = ----π-----. 0 π t(1− t)

Teraz widać drugą niewątpliwą zaletę doświadczenia polegającego na rzutach monetą: umożliwia ono dokonanie przeglądu podstawowych twierdzeń rachunku prawdopodobieństwa.