Mój sposób mierzenia losowości jest zasadny dla gier z kategorii "wyścigów planszowych". Takie gry w uproszczeniu polegają na tym, że kolejno losujemy liczby (na przykład rzucając kością) i chcemy, by suma naszych wylosowanych wartości jak najszybciej osiągnęła lub przekroczyła pewien pułap. Na przykład w Chińczyku, rzucając kośćmi ruszamy pionkiem o wylosowaną liczbę oczek, a żeby wygrać, musimy przesunąć pionki o 166 oczek (jeśli nie zbito naszego pionka). Te gry łączy jedno: nawet jeśli jesteś genialnym strategiem, jeśli będziesz miał pecha, to przegrasz.

W takich grach to, o ile zwiększy się nasza suma, warunkuje pewna zmienna losowa odpowiadająca jednemu losowaniu: będziemy o niej myśleć jak o obiekcie matematycznym, który przyjmuje różne wartości, każdą z pewnym prawdopodobieństwem, a prawdopodobieństwa te sumują się do jedynki. Dla przykładu, jeżeli zmienna losowa 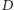reprezentuje wynik rzutu kością sześciościenną, to wartości tej zmiennej razem z prawdopodobieństwami wystąpienia wyglądają tak

Do opisu zmiennych losowych często używamy następujących pojęć: wartości oczekiwanej 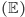oraz wariancji 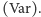Wartość oczekiwana to suma możliwych wartości zmiennej losowej przemnożonych przez prawdopodobieństwo ich uzyskania i odpowiada "przeciętnie" wyrzucanej wartości. Wariancja zmiennej to wartość oczekiwana kwadratu odstępstwa od wartości oczekiwanej tej zmiennej. Dla rzutu kością sześciościenną wartości te są równe

Wariancja zawiera informację, jak zachowują się odchylenia od normy po kilku losowaniach. Należy pamiętać, że obie sumy oczek graczy odchylają się od normy, więc większa wariancja oznacza, że będą się bardziej odchylać od siebie nawzajem, czyli częściej będzie dochodziło do frustracji. Ma ona jednak pewną słabość: załóżmy, że grając w grę, zamiast liczenia wyniku rzutu kością liczymy podwojony wynik rzutu kością. Wtedy wariancja będzie 4 razy większa, natomiast co do zasady nasza gra nie ulegnie przecież specjalnej zmianie. W związku z tym sensownie jest rozważać "unormowaną" wariancję, losowość określoną następującym wzorem

Wyliczając wartość losowości rzutu kością 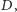otrzymujemy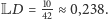

Powróćmy do Chińczyka. W grze rzucamy kością, by zdecydować, jak daleko przesuwamy pionek. Jest to wbudowane w mechanikę gry, nie można do końca na to narzekać. Jednak są dodatkowe zasady, które tej losowości jeszcze pomagają. Ja na przykład często grałem w wariant, w którym gdy gracz wyrzuci szóstkę, to dostaje dodatkowy ruch. Jak zmienia to losowość? Zobaczmy. Niech 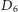będzie zmienną losową, odpowiadającą sumom liczb oczek, które możemy otrzymać, wykonując ruch. Zmiennej tej odpowiada następująca tabelka

Podobnie, jak poprzednio, możemy obliczyć wartość oczekiwaną, wariancję i losowość (choć tym razem wymagałoby to od nas umiejętności sumowania nieskończonego ciągu geometrycznego)

Czyli (drodzy miłośnicy zasady z dodatkowym rzutem) losowość rośnie. Trudno dokładnie powiedzieć, jak wpływa to na doznania płynące z gry, no ale Chińczyk sam w sobie jest losowy, nie dokładajmy mu. Jeżeli jednak ktoś uważa, że zwykłe rzucanie kostką jest nudne, to może zmienić tę zasadę: niechaj dodatkowy ruch przysługuje po wyrzuceniu jedynki. Czy takie losowanie jest lepsze? Zobaczmy. Nazwijmy je 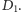Odpowiednia tabelka dla tej zmiennej wygląda następująco

Jaka jest wartość oczekiwana, wariancja i losowość?

Losowość zmalała, więc widać, że dodanie fikuśnej zasady z podwójnym ruchem nie musi psuć gry. Równość wartości oczekiwanych 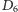i 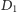może natomiast wydawać się zaskakująca - zwróćmy bowiem uwagę, że w tym pierwszym przypadku za każdym powtórzonym rzutem przesuwamy się o więcej niż w drugim przypadku. Zauważmy jednak, że wartość oczekiwana 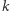-tego rzutu jest w obu przypadkach taka sama i wynosi 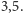Ponadto prawdopodobieństwo wystąpienia 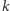-tego rzutu też jest w obu przypadkach to samo i wynosi 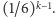W tej sytuacji wartości oczekiwane sumarycznej liczby wyrzuconych oczek również muszą się zgadzać.

Mam nadzieję zagrać w Chińczyka na tych zasadach i zobaczyć, czy odczuję różnicę. Polecam Czytelnikom zmienianie dobrze znanych im gier w imię zmniejszenia losowości.