Paccioli uważał, że w sytuacji opisanej w historyjce nagroda powinna zostać podzielona w stosunku takim, jak stosunek liczby punktów zdobytych przez graczy, czyli 3 do 5 ( 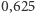puli przyznajemy Jackowi). Innego zdania był Girolamo Cardano (1501-1576), ten sam, którego imię noszą (nie do końca słusznie) wzory na rozwiązania równań 3. i 4. stopnia. W swym dziele Practica Arithmeticae Generalis stwierdza, że w sytuacji, gdy jednemu z graczy brakuje do zwycięstwa 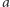punktów, a drugiemu 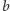punktów, cała stawka powinna być podzielona w stosunku 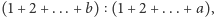czyli u nas 15:28 (do Jacka wędruje 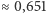stawki). Wśród próbujących rozwikłać problem podziału należy wymienić jeszcze słynnego antagonistę Cardana, czyli Niccola Tartaglię. Zwraca on słusznie uwagę, że podejście Luki Paccioliego nie może być sensowne, gdyż przy wyniku 0:1 kazałoby przeznaczyć całą stawkę jednemu z graczy, chociaż drugi ma niewiele mniejszą szansę na wygraną. Odpowiedź proponowana przez Tartaglię nie jest jednak specjalnie lepsza, gdyż proponuje on, by zwycięzca otrzymał pół stawki powiększone o połowę względnej różnicy w punktach (czyli w tym przypadku 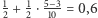). Nie jest to jednak dobre podejście, gdyż podzieliłoby stawkę w ten sam sposób przy wyniku 9:7, w którym (jak nietrudno obliczyć) szansa drugiego gracza na wygraną wynosi 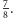Problem podziału stawki doczekał się prawidłowego (tzn. opartego na prawdopodobieństwach wygranych poszczególnych graczy) rozwiązania dopiero w połowie XVII wieku, kiedy został podsunięty Blaise'owi Pascalowi (1623-1662) przez Antoine'a Gombauda (1607-1684), znanego szerzej jako kawaler de Méré. Pascal korespondował na ten temat z Pierrem Fermatem (1601-1665) i wspólnie udało im się wskazać rozwiązanie (rozumowanie opisane w wierszyku pochodzi od Fermata, rozwiązanie Pascala nie wymagało "przedłużania" gry po wygranej któregoś z graczy, wykorzystywało natomiast pewne własności trójkąta Pascala).

Inną zagadką, zadaną Pascalowi przez kawalera de Méré, było pytanie o najmniejszą liczbę rzutów dwiema kośćmi, potrzebną do tego, aby z prawdopodobieństwem przewyższającym 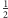wyrzucić za którymś razem dwie szóstki. De Méré potrafił rozwiązać to zadanie w przypadku rzutu jedną kością - w tym celu wystarczy skoncentrować uwagę na zdarzeniu przeciwnym do rozważanego, czyli pytaniu o najmniejszą liczbę rzutów, przy której szansa na uniknięcie szóstki jest mniejsza od 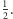Ponieważ w pojedynczym rzucie szansa na uniknięcie szóstki wynosi 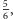zatem szansa na niewyrzucenie szóstki w rzutach wynosi 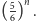Szukamy zatem najmniejszej wartości 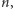dla której 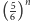jest mniejsze od 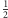; nietrudno sprawdzić, że liczba ta wynosi 4. W jaki sposób rozszerzyć to rozumowanie na rzut dwiema kośćmi? Tutaj kawaler de Méré napotkał trudności, gdyż był zdania, że stosunek szukanej "wartości granicznej" do liczby wszystkich możliwości powinien być stały, zatem skoro w przypadku jednego rzutu był on jak 4 (wartość graniczna) do 6 (liczba możliwości), to skoro przy dwóch rzutach mamy 36 równo prawdopodobnych możliwości (z czego de Méré zdawał sobie sprawę), poszukiwana "wartość graniczna" w tym przypadku wynosi 24. De Méré nie poprzestał jednak na teorii i postanowił sprawdzić ją w praktyce - ta miała jednak inne zdanie na ten temat i mocno sugerowała, że po 24 rzutach dwie szóstki zdarzają się rzadziej niż częściej. O tej rozbieżności poinformował Pascala, twierdząc, że jego odkrycie oznacza sprzeczność arytmetyki. Pascal nie miał jednak trudności w dostrzeżeniu, w czym tkwi paradoks. Kluczem do rozwiązania jest najrozsądniejsza ocena szansy na uniknięcie dwóch szóstek w jednym, podwójnym rzucie - jest to, oczywiście, 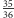(gdyż szansa na dwie szóstki to 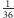). W tej sytuacji, podobnie jak poprzednio, szukamy najmniejszej wartości 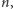dla której 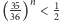- tym razem wychodzi 25. Szansa na wyrzucenie dwóch szóstek po takiej liczbie rzutów wynosi w przybliżeniu 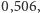podczas gdy szansa na dwie szóstki po 24 rzutach to około 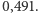Kawaler de Méré musiał zatem wykonać całkiem pokaźną liczbę doświadczeń, aby stwierdzić, że w praktyce liczba 24 jest zbyt mała…

Przedstawione problemy opierają się na pojęciach współcześnie elementarnych (jak np. prawdopodobieństwo), z którymi ludzkość oswajała się dość długo i które w czasach, w jakich były "wykuwane", dostarczały trudności z dzisiejszego punktu widzenia elementarnych. Ciekawie jest zastanowić się, czy za paręset lat, w jubileuszowym, pięciotysięcznym numerze Delty, przyszli autorzy artykułów będą mogli z pewnym rozbawieniem opisywać nasze mniej lub bardziej udolne próby rozwiązania pewnych skomplikowanych dziś problemów, które już wtedy będą uznawane za zupełnie banalne...