Powiedzmy, że mamy do dyspozycji 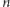kart, które ponumerowaliśmy liczbami naturalnymi. Gdy przyporządkujemy kartom ich pozycje, to szybko zauważymy, że ta reprezentacja prowadzi nas do interpretacji potasowanej talii jako permutacji zbioru 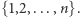Teraz możemy zastanowić się, jaki jest cel tasowania kart i opisać dobre potasowanie w języku probabilistyki. Skoro potasowana talia 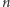kart może być potraktowana jako permutacja, to mówiąc o dobrym tasowaniu, zapewne mamy na myśli, że po potasowaniu kart otrzymamy dowolną permutację z jednakowym prawdopodobieństwem. Na przykład dla talii 3 kart każda z sześciu możliwości ich potasowania 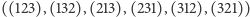powinna wypadać - średnio - raz na sześć tasowań.

Zbadajmy teraz pewne proste tasowanie: w każdym ruchu bierzemy kartę z wierzchu i wkładamy ją na losowe miejsce w talii (a jakżeby inaczej: z jednakowym prawdopodobieństwem!). Pokażemy, że jeżeli oznaczymy kartę leżącą na spodzie stosu kart, a następnie będziemy tasować do momentu, aż oznaczona karta trafi na wierzch i jeszcze jeden ruch dłużej, to otrzymamy losową (w przedstawionym wyżej sensie) talię. Pomysł wygląda prosto, ale jak sprawdzić, że działa? Żeby przekonać się o jego skuteczności, podzielmy nasze tasowanie na drobniejsze kroki:

• 1. Tasujemy do momentu, aż pewna karta znajdzie się pod oznaczoną kartą.
• 2. Tasujemy do momentu, aż dwie karty znajdą się pod oznaczoną kartą.
• ...
• n - 1. Tasujemy do momentu, aż 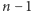kart znajdzie się pod oznaczoną kartą.
• n. Wkładamy oznaczoną kartę (znajdującą się w tym momencie na wierzchu) w dowolne miejsce talii z jednakowym prawdopodobieństwem.

Teraz możemy uzasadnić, że po każdym kroku karty znajdujące się pod kartą oznaczoną są dobrze potasowane.

• 1. Nie ulega wątpliwości, że po pierwszym kroku karty znajdujące się pod tą oznaczoną są dobrze potasowane (jest wszak tylko jedna...).
• 2. A zatem: nie ulega wątpliwości, że po drugim kroku 2 karty znajdujące się pod tą oznaczoną są dobrze potasowane (karta z wierzchu z takim samym prawdopodobieństwem znajdzie się pod i nad pierwszą kartą, która trafiła pod oznaczoną kartę)
• i. Rozumując indukcyjnie, zakładamy, że po kroku 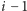pod oznaczoną kartą znajduje się 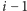dobrze potasowanych kart. Jeśli po 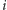-tym kroku pierwsza z brzegu karta została losowo umieszczona w talii i wiemy, że wylądowała pod oznaczoną kartą, to innymi słowy została losowo umieszczona wśród kart znajdujących się pod tą oznaczoną, a zatem po wykonaniu 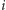-tego kroku pod oznaczoną kartą znajduje się 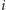dobrze potasowanych kart.
• ...
• n - 1. A zatem: nie ulega wątpliwości, że po 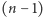-szym kroku 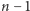kart znajdujących się pod oznaczoną kartą jest dobrze potasowanych.
• n. A zatem: nie ulega wątpliwości, że po 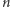-tym kroku talia kart jest dobrze potasowana.

Skoro znamy już opis kroków, to chcielibyśmy powiedzieć coś o liczbie ruchów, które musimy wykonać w tym tasowaniu, zanim uzyskamy idealnie potasowaną talię. Oznaczmy tę liczbę przez 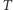; oczywiście, jest to wielkość losowa, spróbujemy jednak obliczyć jej średnią. Niech 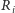będzie liczbą ruchów potrzebną na wykonanie 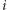-tego kroku. Wówczas 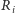ma rozkład geometryczny z parametrem 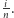Istotnie, po 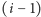-szym kroku prawdopodobieństwo umieszczenia pierwszej z brzegu karty pod kartą oznaczoną (zatem wykonania 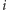-tego kroku) wynosi właśnie 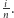Teraz możemy obliczyć średnią 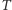; wystarczy zauważyć, że 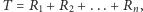a zatem:

Przy użyciu powyższego wzoru możemy oszacować średnią liczbę ruchów potrzebną do dobrego potasowania przedstawionym schematem talii 52 kart przez 205. W rzeczywistości, aby mieć dużą pewność co do skuteczności tego tasowania, wymagane jest około 300 ruchów.

Oczywiście, przedstawiony sposób tasowania nie należy do szczególnie popularnych. O wiele częściej można spotkać tzw. overhand shuffle, którego matematyczny model można wyrazić w następujący sposób: na początku w każdą z 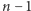luk między kartami wstawiamy z ustalonym prawdopodobieństwem 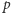"przegródkę", tworząc w ten sposób pewną losową liczbę bloków, a następnie odwracamy ich kolejność. Taki schemat tasowania uchodzi za amatorski i dużo bardziej profesjonalnie prezentuje się tzw. riffle shuffle. W języku matematycznym może on zostać przedstawiony następująco: najpierw każdemu miejscu w talii przyporządkowujemy 1 lub 0 z równymi prawdopodobieństwami, a następnie na miejscu 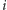-tej "jedynki" od góry umieszczamy 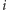-tą kartę od góry, a na miejscu 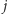-tego "zera" od dołu 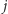-tą kartę od dołu. Podczas analizy tego sposobu tasowania często wygodniej jest posłużyć się prostszym opisem procedury "odtasowywania", polegającej na losowym przyporządkowaniu kartom 0 i 1, a następnie umieszczeniu bloku kart "jedynkowych" przed blokiem kart "zerowych".

Profesor Persi Diaconis, który zajmuje się tą tematyką, pokazuje w swoich artykułach, że overhand shuffle wymaga średnio 10 000 ruchów do dobrego potasowania, zatem przedstawiony przez nas pozornie naiwny sposób tasowania jest lepszy od tego, jakim posługuje się wiele osób (przynajmniej w opisanym przez nas sensie). Z drugiej strony, tym, którzy stosują riffle shuffle, wystarczy średnio 7 ruchów, aby tasowanie było dobre. Warto zatem nauczyć się tego sposobu tasowania, nie tylko ze względu na jego efektowność.

Na koniec kilka uzupełnień. Powyżej opisaliśmy losowy czas 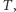po którym rozkład potasowanej talii (na pewno!) będzie jednostajny. W teorii taki czas nazywamy mocnym czasem jednostajnym (ang. strong uniform time). Wyznaczanie jego średniej stanowi dopiero początek rozważań. Celem wielu współczesnych analiz jest znalezienie takiej liczby tasowań, która z dużym prawdopodobieństwem pozwoli osiągnąć "wystarczająco dobre" potasowanie (tzn. chcemy, aby po ustalonym czasie uzyskany rozkład prawdopodobieństwa był odpowiednio bliski rozkładowi jednostajnemu) - w tej sytuacji mówi się o czasie mieszania (ang. mixing time).

Udanych tasowań i rozdań!