Kluska w uchu wielbłąda albo arytmetyka moralna
Powiada Ewangelia: Łatwiej jest wielbłądowi przejść przez ucho igielne, niż bogatemu wejść do królestwa niebieskiego.

Rys. 1
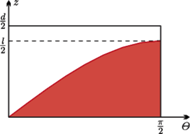
Rys. 2
Lingwiści, i nie tylko oni, próbują znaleźć jakieś sensowne wyjaśnienie tych słów. Na przykład Cyryl Aleksandryjski twierdził, że jest to językowe nieporozumienie, a Jezus miał w rzeczywistości na myśli nie wielbłąda, lecz linę. Oba te wyrazy mogły być pomylone z powodu zachodzącego w języku greckim procesu nazwanego itacyzmem. Polegał on na zamianie litery 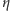 na literę
na literę  (
( 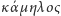 to wielbłąd, natomiast
to wielbłąd, natomiast 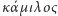 to lina). Jest to tym bardziej prawdopodobne, że aramejskie słowo gamla oznaczało zarówno samego wielbłąda, jak i wykonaną z jego sierści linę. Jak to często bywa, winny jest niedouczony interpretator.
to lina). Jest to tym bardziej prawdopodobne, że aramejskie słowo gamla oznaczało zarówno samego wielbłąda, jak i wykonaną z jego sierści linę. Jak to często bywa, winny jest niedouczony interpretator.
Rys. 3
Z podobną grą słów mamy do czynienia w pewnym ciekawym zagadnieniu dotyczącym rachunku prawdopodobieństwa. Aby je omówić, zaczniemy od rzeczy powszechnie znanej, czyli od igły Buffona, opisanej przezeń w 1777 roku w Szkicu o arytmetyce moralnej. Rzucamy igłą o długości 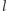 na płaszczyznę podzieloną równoległymi liniami, przy czym odległość
na płaszczyznę podzieloną równoległymi liniami, przy czym odległość 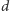 między sąsiednimi liniami spełnia warunek
między sąsiednimi liniami spełnia warunek 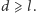 Niech
Niech  oznacza odległość igły od najbliższej linii, natomiast
oznacza odległość igły od najbliższej linii, natomiast 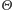 mniejszy z kątów, jaki igła tworzy z tą linią. Możliwe wartości
mniejszy z kątów, jaki igła tworzy z tą linią. Możliwe wartości  i
i 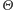 leżą w przedziałach, odpowiednio,
leżą w przedziałach, odpowiednio, ![|[0, d2]](/math/temat/matematyka/rachunek_prawdopodobienstwa/2016/05/26/Kluska_w_uchu_wielblada/8x-f4fa4b0dd944a9a9c6e47301280fed62c4a88e5b-im-33,33,33-FF,FF,FF.gif) i
i ![[0,π 2].](/math/temat/matematyka/rachunek_prawdopodobienstwa/2016/05/26/Kluska_w_uchu_wielblada/9x-f4fa4b0dd944a9a9c6e47301280fed62c4a88e5b-im-33,33,33-FF,FF,FF.gif) Przyjmujemy, że
Przyjmujemy, że  i
i 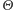 są niezależnymi zmiennymi losowymi o rozkładach jednostajnych. Długość rzutu igły na kierunek prostopadły do linii jest równa
są niezależnymi zmiennymi losowymi o rozkładach jednostajnych. Długość rzutu igły na kierunek prostopadły do linii jest równa 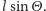 Jeżeli środek igły jest odległy od najbliższej linii o mniej niż
Jeżeli środek igły jest odległy od najbliższej linii o mniej niż 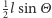 (Rys. 1), to igła przecina linię. Prawdopodobieństwo przecięcia linii jest więc równe stosunkowi pola
(Rys. 1), to igła przecina linię. Prawdopodobieństwo przecięcia linii jest więc równe stosunkowi pola 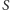 pod sinusoidą
pod sinusoidą 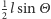 i pola prostokąta o bokach
i pola prostokąta o bokach 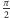 i
i 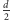 (Rys. 2).
(Rys. 2).
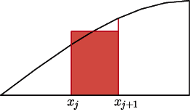
Pole 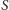 możemy obliczyć, dzieląc odcinek
możemy obliczyć, dzieląc odcinek ![π [0, 2]](/math/temat/matematyka/rachunek_prawdopodobienstwa/2016/05/26/Kluska_w_uchu_wielblada/2x-072feb7e0634f093665635342a05657e3c0dac00-im-33,33,33-FF,FF,FF.gif) na
na 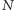 małych odcinków. Niech
małych odcinków. Niech 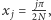
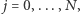 będą końcami kolejnych odcinków. Wtedy
będą końcami kolejnych odcinków. Wtedy 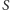 przybliżamy jako
przybliżamy jako

Szukane prawdopodobieństwo jest równe 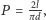 a w szczególności dla
a w szczególności dla 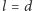 otrzymujemy
otrzymujemy 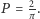 Wynik ten pozwala "zmierzyć" wartość liczby
Wynik ten pozwala "zmierzyć" wartość liczby 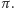 Nie trzeba rzucać prawdziwą igłą, wystarczy "doświadczenie komputerowe". Jeśli posłużymy się definicją prawdopodobieństwa podaną przez Laplace'a, to dla
Nie trzeba rzucać prawdziwą igłą, wystarczy "doświadczenie komputerowe". Jeśli posłużymy się definicją prawdopodobieństwa podaną przez Laplace'a, to dla 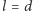 mamy
mamy

gdzie 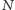 to liczba rzutów, a
to liczba rzutów, a 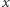 to liczba przecięć. Ponieważ przyjęliśmy (arbitralnie?) jednostajność obu rozkładów, można też twierdzić, że w rzeczywistości nie tyle wyznaczamy wartość
to liczba przecięć. Ponieważ przyjęliśmy (arbitralnie?) jednostajność obu rozkładów, można też twierdzić, że w rzeczywistości nie tyle wyznaczamy wartość 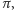 ile testujemy to założenie.
ile testujemy to założenie.
Wszystkim, których zdumiewa obecność liczby  w zadaniu dotyczącym rachunku prawdopodobieństwa, Hugo Steinhaus wyjaśniał w charakterystycznym dla siebie stylu, że jest to ilustracja powiedzenia fortuna kołem się toczy. Jednak w rzeczywistości to nie powinno dziwić. Liczba
w zadaniu dotyczącym rachunku prawdopodobieństwa, Hugo Steinhaus wyjaśniał w charakterystycznym dla siebie stylu, że jest to ilustracja powiedzenia fortuna kołem się toczy. Jednak w rzeczywistości to nie powinno dziwić. Liczba 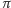 jest zdefiniowana jako stosunek długości okręgu do jego średnicy. Zauważmy, że wszystkie możliwe położenia jednego końca igły względem drugiego tworzą okrąg, którego promień jest długością tej igły. A zatem jesteśmy w domu.
jest zdefiniowana jako stosunek długości okręgu do jego średnicy. Zauważmy, że wszystkie możliwe położenia jednego końca igły względem drugiego tworzą okrąg, którego promień jest długością tej igły. A zatem jesteśmy w domu.
A teraz zrobimy z liny ewangelicznego wielbłąda. A raczej z igły Buffona uczynimy matematyczną linę albo kluskę. Podamy rozwiązanie podobnego zagadnienia, którego autorem jest Joseph-Émile Barbier. Ta wersja problemu igły Buffona (ang. Buffon's needle) nosi żartobliwą nazwę kluski Buffona (ang. Buffon's noodle).
W przypadku 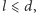 który tu rozważamy, możliwe jest co najwyżej jedno przecięcie igły z linią. Wprowadzimy nową zmienną losową przyjmującą wartość 1, gdy igła przecina linię, i 0, gdy igła nie przecina linii. Obliczmy wartość średnią tej zmiennej. Jest ona równa
który tu rozważamy, możliwe jest co najwyżej jedno przecięcie igły z linią. Wprowadzimy nową zmienną losową przyjmującą wartość 1, gdy igła przecina linię, i 0, gdy igła nie przecina linii. Obliczmy wartość średnią tej zmiennej. Jest ona równa

Widzimy, że jest to prawdopodobieństwo przecięcia linii przez igłę. Wyrażenie po prawej stronie powyższego równania jest zarazem średnią liczbą przecięć, 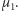 Zastąpimy teraz igłę przez łamaną złożoną z
Zastąpimy teraz igłę przez łamaną złożoną z 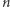 odcinków. Niech
odcinków. Niech 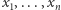 będą liczbami przecięć linii przez te odcinki, natomiast
będą liczbami przecięć linii przez te odcinki, natomiast 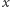 ich sumą, czyli liczbą przecięć linii przez łamaną. Wielkości
ich sumą, czyli liczbą przecięć linii przez łamaną. Wielkości 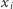 nie są niezależnymi zmiennymi losowymi, ale to bez znaczenia, bo średnia liczba przecięć linii przez łamaną i tak jest sumą średnich liczb przecięć linii przez odcinki
nie są niezależnymi zmiennymi losowymi, ale to bez znaczenia, bo średnia liczba przecięć linii przez łamaną i tak jest sumą średnich liczb przecięć linii przez odcinki

Przejdziemy teraz z łamaną do granicznej krzywej gładkiej (czyli naszej kluski) o ustalonej długości, zwiększając do nieskończoności liczbę odcinków łamanej. Średnia liczba przecięć kluski jest proporcjonalna do jej długości 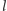 i wynosi tyle samo co dla igły Buffona:
i wynosi tyle samo co dla igły Buffona:

Swoją drogą, Barbier udowodnił w rzeczywistości coś więcej, bo nazwane jego imieniem twierdzenie, które mówi, że dla dowolnej zamkniętej krzywej o stałej szerokości stosunek jej długości do jej średnicy zawsze jest taki sam i równy 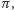 niezależnie od kształtu tej krzywej.
niezależnie od kształtu tej krzywej.
Rozwiązanie zagadnienia Buffona wielokrotnie testowano eksperymentalnie. Wspomnimy tu o jednym tylko wyniku, uzyskanym w 1901 roku przez włoskiego matematyka Mario Lazzariniego, który rzucał 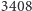 razy igłą o stosunku długości do szerokości paska równym
razy igłą o stosunku długości do szerokości paska równym 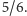 W tym przypadku
W tym przypadku 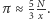 Lazzarini uzyskał robiący wrażenie rezultat o błędzie mniejszym od
Lazzarini uzyskał robiący wrażenie rezultat o błędzie mniejszym od 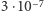 ; było to przybliżenie
; było to przybliżenie 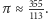 Podejrzenie wzbudził jednak fakt, że powyższe przybliżenie znane jest od dawna jako najlepsze wymierne przybliżenie
Podejrzenie wzbudził jednak fakt, że powyższe przybliżenie znane jest od dawna jako najlepsze wymierne przybliżenie 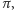 jeśli ograniczyć się do liczb co najwyżej pięciocyfrowych. Jeśli spełniony jest warunek
jeśli ograniczyć się do liczb co najwyżej pięciocyfrowych. Jeśli spełniony jest warunek 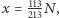 to otrzymamy właśnie owo wspomniane najlepsze przybliżenie. Łatwo tego dokonać. Wystarczy wybrać liczbę
to otrzymamy właśnie owo wspomniane najlepsze przybliżenie. Łatwo tego dokonać. Wystarczy wybrać liczbę 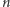 będącą wielokrotnością liczby
będącą wielokrotnością liczby 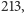 a wtedy
a wtedy 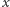 jest liczbą całkowitą. Liczba
jest liczbą całkowitą. Liczba 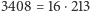 jest taką wielokrotnością. Dziś uważa się wynik Lazzariniego za oszustwo (co jest przecież rzeczą niemoralną) albo raczej za wyrafinowany żart (a to już zupełnie inna sprawa).
jest taką wielokrotnością. Dziś uważa się wynik Lazzariniego za oszustwo (co jest przecież rzeczą niemoralną) albo raczej za wyrafinowany żart (a to już zupełnie inna sprawa).
W tytule oryginalnej pracy Buffona występuje nazwa arytmetyka moralna. Pojęcie to wywodzi się z chętnie praktykowanej przez Anglosasów (a zwalczanej przez myślicieli chrześcijańskich) filozofii utylitaryzmu (Bentham), która uczy, że o moralnej wartości czynu świadczą jedynie jego skutki. Stąd, podejmując decyzje moralne, jesteśmy zmuszeni dokonywać swoistego rachunku użyteczności, czyli arytmetyki albo buchalterii moralnej, i szacować miarę pozytywnych oraz negatywnych skutków naszych czynów. Propozycja rozstrzygania konfliktu wartości i określenia moralnego obowiązku w oparciu o ową buchalterię moralną opiera się na (naiwnym z dzisiejszego punktu widzenia) założeniu, że możliwe jest odkrycie jakiejś wspólnej miary dla wszystkich ludzkich wartości i że taki uniwersalny zbiór niewykluczających się wzajemnie wartości istnieje.
Ewangelista, być może, powiedziałby, że miarą jest ucho igielne...