Prowadzący grę zna położenie kart i zawsze odkrywa kartę różną od Asa. Jeżeli ma do wyboru Króla albo Damę, pokazuje Króla z prawdopodobieństwem 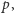a Damę z prawdopodobieństwem 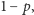gdzie 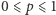(np. można wyobrazić sobie sytuację, gdy prowadzący grę bardzo lubi Króla - wtedy 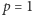). Następnie odkrywa kartę i jest nią Król.

Oblicz prawdopodobieństwo sukcesu gracza, który zmieni swój pierwotny wybór.

Często spotykamy takie rozumowania:

1)

Zostały dwie karty, As i Dama. Jedną z nich ma prowadzący grę, a drugą gracz. Jest więc wszystko jedno, czy gracz zmieni swój wybór czy nie, prawdopodobieństwo wygranej jest równe

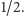
2)

Prawdopodobieństwo tego, że gracz pierwotnie wskazał Asa, jest równe 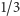i pokazanie Króla nic nie zmienia. Stąd wynika, że prawdopodobieństwo sukcesu gracza, który zmieni swój wybór, jest równe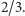

Są to dwa różne rozumowania, które znacznie upraszczają problem. Oba pomijają informację o odkrytej karcie, ignorują preferencje prowadzącego grę i prowadzą do dwóch różnych wyników.

Aby rozwiązać ten problem, zbudujemy model probabilistyczny dla tego doświadczenia.

Mamy cztery możliwości, które przedstawiamy w tabeli.

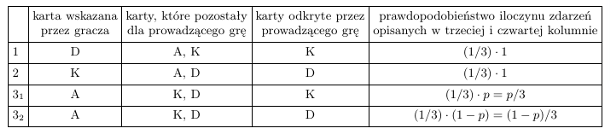
Oznaczmy przez 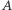zdarzenie losowe polegające na tym, że gracz nie wskazał Asa i osiągnie sukces po zmianie swojego pierwotnego wyboru, i przez 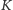zdarzenie losowe polegające na tym, że prowadzący grę odkryje Króla.

Mamy obliczyć prawdopodobieństwo warunkowe, czyli

Z pierwszego wiersza tabeli mamy 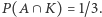Prawdopodobieństwo zdarzenia polegającego na tym, że prowadzący odkryje Króla, jest równe

czyli sumie prawdopodobieństw z pierwszego i trzeciego wiersza. Stąd

zatem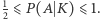

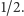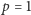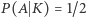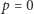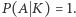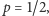Prawdopodobieństwo wygranej gracza przy zamianie kart jest nie mniejsze od Gdy (prowadzący bardzo lubi Króla), to ; gdy (prowadzący bardzo lubi Damę i odkrył Króla, czyli gracz ma Damę), to Gdy mamy 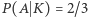; przypadek ten oznacza, że prowadzący grę - w sytuacji, gdy ma do wyboru Króla albo Damę - wybiera kartę losowo.