Drobiazgi
Prawdopodobieństwo i podzielność
Wybieramy jedną liczbę ze zbioru 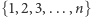 tak, że prawdopodobieństwo wyboru liczby
tak, że prawdopodobieństwo wyboru liczby 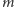 z tego zbioru jest równe
z tego zbioru jest równe 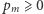 i
i 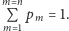
Określamy dla 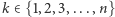 zdarzenia losowe
zdarzenia losowe 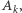 polegające na tym, że wylosowana liczba jest podzielna przez
polegające na tym, że wylosowana liczba jest podzielna przez 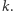
Rozważmy następujący problem:
Problem. Dla jakich 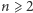 można określić liczby
można określić liczby 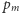 tak, aby dla wszystkich
tak, aby dla wszystkich 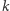 było
było 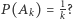
Wydaje się, że jest to możliwe dla bardzo wielu 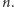 Można jednak to zrobić tylko dla
Można jednak to zrobić tylko dla 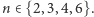
- Dla
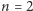 mamy
mamy 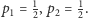
- Dla
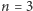 mamy
mamy 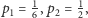
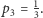
- Dla
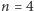 mamy
mamy 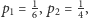
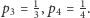
- Dla
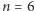 mamy
mamy 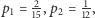
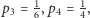
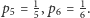
Zachęcam Czytelnika do kontynuacji próby określenia liczb 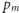 dla
dla 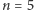 :
: