Drobiazgi

Niezależność zdarzeń w modelu klasycznym

W teorii prawdopodobieństwa mówimy o modelu klasycznym, gdy zbiór wszystkich zdarzeń elementarnych 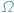$Ω$ jest zbiorem skończonym i wszystkie zdarzenia jednoelementowe są jednakowo prawdopodobne...

W modelu klasycznym dla każdego zdarzenia losowego 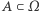$A$ prawdopodobieństwo tego zdarzenia jest równe:

P(A)

Zdarzenia losowe 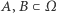$A,$ są niezależne, gdy 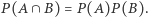$|P(A$ Zdarzenie losowe 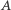$A$ będziemy nazywali nietrywialnym, gdy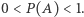 $0 | < P(A)$

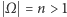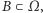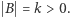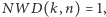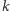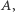Rozważmy model klasyczny, w którym $Ω$ i takie zdarzenie losowe $|B ⊂Ω$ że $| B = k > 0.$ Czytelnikowi sugerujemy przeprowadzenie dowodu (np. metodą nie wprost) następującego faktu: jeżeli $WD(k,n)=1, |N$ tzn. liczby $|k$ oraz $n$ są względnie pierwsze, to nie istnieje nietrywialne zdarzenie losowe $A,$ które jest niezależne z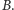 $B. |$

Z tego faktu wynika wniosek: jeżeli 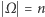$Ω$ jest liczbą pierwszą, to nie istnieją dwa zdarzenia losowe 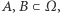$A,$ które są nietrywialne i niezależne.

Czyżby grający w amerykańską ruletkę o 37 polach o tym nie wiedzieli?