Pierwsza, 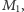ma orły po obu stronach, druga, 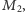ma reszki po obu stronach, a trzecia, 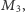jest normalna. Wybrano losowo jedną z tych monet, podrzucono ją i po upadku na blat stołu na wierzchu ukazał się orzeł. Należy obliczyć prawdopodobieństwo tego, że po drugiej stronie tej monety też jest orzeł. Często spotykamy takie rozwiązanie:

(1)

Na pewno nie jest to moneta 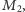która ma reszki po obu stronach. Prawda.

(2)

Jest to więc moneta 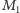albo 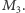Prawda.

(3)

Stąd wynika, że prawdopodobieństwo tego, że jest to moneta 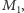jest równe 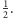Nieprawda. Przypadki opisane w podpunkcie 2 nie są jednakowo prawdopodobne.

Aby się o tym przekonać, sformalizujmy nasz problem. Wprowadźmy oznaczenia dla zdarzeń:

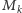- wylosujemy monetę o numerze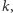

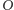- otrzymamy orła.

Z treści zadania wynika, że 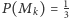i 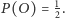Mamy obliczyć prawdopodobieństwo warunkowe :

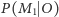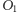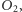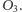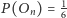Ten wynik nie powinien być zaskakujący. Oznaczmy orły na pierwszej monecie przez oraz a orła na trzeciej monecie przez Prawdopodobieństwo otrzymania orła z numerem jest równe dla 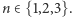Otrzymaliśmy jedno z trzech jednakowo prawdopodobnych zdarzeń 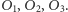Dwa spośród nich wskazują na pierwszą monetę. Czytelnik Dociekliwy zauważy, że ten sam wynik otrzymamy w przypadku, gdy trzecia moneta jest symetryczna, a pozostałe dwie niekoniecznie.