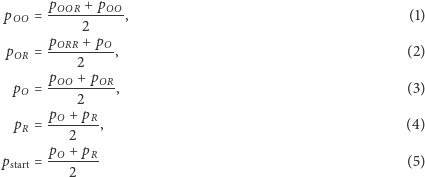RROzważania O RReszce i ORRle
Zwykła moneta często okazuje się doskonałym narzędziem do rozstrzygania konfliktów. Zapewne każdemu zdarzyło się usłyszeć magiczną formułkę "orzeł to, reszka tamto", z reguły będąc przychylnym dokładnie jednemu ze zdarzeń "to" lub "tamto". Takie rozwiązanie jest jednak mało widowiskowe - o ile wzajemne obrzucanie się inwektywami (w celu wytłumaczenia, w jak wielkim błędzie jest strona przeciwna, prezentując zdanie odmienne od naszego) szybko przyciąga publiczność, tak zakończenie sporu przy użyciu jednego rzutu monetą może pozostawić ją z odczuciem niedosytu.
Rys. 1
Przykładowym sposobem na uatrakcyjnienie oraz niewielkie przedłużenie całej procedury jest rzucanie monetą, dopóki wśród kolejnych wyników nie pojawi się jedna z konfiguracji 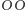 lub
lub 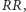 w zależności od której wyłaniany jest zwycięzca. Ich oczywista symetria sprawia, że przegrany może czuć się pokrzywdzony jedynie przez los, nie zaś przez oszustne praktyki adwersarza. Co jednak, jeśli osoba typująca
w zależności od której wyłaniany jest zwycięzca. Ich oczywista symetria sprawia, że przegrany może czuć się pokrzywdzony jedynie przez los, nie zaś przez oszustne praktyki adwersarza. Co jednak, jeśli osoba typująca 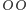 (nazwijmy ją Jackiem) zmieniła zdanie na
(nazwijmy ją Jackiem) zmieniła zdanie na 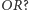 Wówczas obstawiający
Wówczas obstawiający 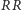 (Placek, rzecz jasna) miałby prawo do słusznego protestu; zauważmy bowiem, że jeśli w pierwszym rzucie pojawi się reszka, to szanse Jacka na zwycięstwo wynoszą
(Placek, rzecz jasna) miałby prawo do słusznego protestu; zauważmy bowiem, że jeśli w pierwszym rzucie pojawi się reszka, to szanse Jacka na zwycięstwo wynoszą 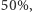 jeśli natomiast orzeł, to wygra on z pewnością (w momencie, w którym pojawi sie pierwsza reszka) i dlatego prawdopodobieństwo jego sukcesu należy oceniać na
jeśli natomiast orzeł, to wygra on z pewnością (w momencie, w którym pojawi sie pierwsza reszka) i dlatego prawdopodobieństwo jego sukcesu należy oceniać na 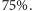 Podobna sytuacja ma miejsce, jeśli Jacek i Placek będą oczekiwać odpowiednio na konfiguracje
Podobna sytuacja ma miejsce, jeśli Jacek i Placek będą oczekiwać odpowiednio na konfiguracje 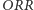 i
i 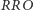 - wbrew pozorom, jakie stwarza równa liczba reszek w obu przypadkach, Jacek jest faworytem również takiej rozgrywki. Wytłumaczenie tego faktu jest analogiczne, jednak odrobinę bardziej skomplikowane, dlatego warto podeprzeć się rysunkiem 1, ilustrującym wszystkie istotne z punktu widzenia rozgrywki "końcówki" ciągu wyników (będziemy je nazywać stanami) oraz strzałki prezentujące możliwość bezpośredniego przejścia między stanami (każde z prawdopodobieństwem
- wbrew pozorom, jakie stwarza równa liczba reszek w obu przypadkach, Jacek jest faworytem również takiej rozgrywki. Wytłumaczenie tego faktu jest analogiczne, jednak odrobinę bardziej skomplikowane, dlatego warto podeprzeć się rysunkiem 1, ilustrującym wszystkie istotne z punktu widzenia rozgrywki "końcówki" ciągu wyników (będziemy je nazywać stanami) oraz strzałki prezentujące możliwość bezpośredniego przejścia między stanami (każde z prawdopodobieństwem 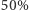 ). Tak jak poprzednio, ciąg rzutów rozpoczynający się od orła nie może skończyć się inaczej niż zwycięstwem Jacka; z kolei gdy zaczniemy od reszki, decydujący jest drugi rzut: reszka prowadzić będzie nieuchronnie do wygranej Placka, natomiast orzeł do Jacka. Wnioskujemy stąd, że ponownie z prawdopodobieństwem
). Tak jak poprzednio, ciąg rzutów rozpoczynający się od orła nie może skończyć się inaczej niż zwycięstwem Jacka; z kolei gdy zaczniemy od reszki, decydujący jest drugi rzut: reszka prowadzić będzie nieuchronnie do wygranej Placka, natomiast orzeł do Jacka. Wnioskujemy stąd, że ponownie z prawdopodobieństwem 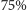 ten ostatni okaże się zwycięzcą.
ten ostatni okaże się zwycięzcą.
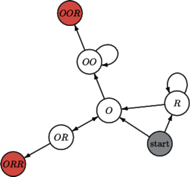
Rys. 2
Co zatem może uczynić Placek, by szala zwycięstwa przechyliła się na jego stronę? Okazuje się, że w celu uzyskania przewagi powinien obstawić konfigurację 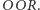 W konfrontacji z
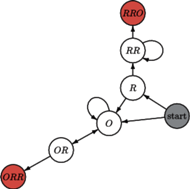
W konfrontacji z 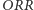 otrzymujemy wówczas stany zilustrowane na rysunku 2. Analiza otrzymanego grafu pozwala szybko przekonać się o przewadze konfiguracji
otrzymujemy wówczas stany zilustrowane na rysunku 2. Analiza otrzymanego grafu pozwala szybko przekonać się o przewadze konfiguracji 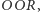 gdyż aby gra się zakończyła, z pewnością musi przejść przez stan
gdyż aby gra się zakończyła, z pewnością musi przejść przez stan 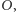 z którego - jeśli przejdzie do stanu
z którego - jeśli przejdzie do stanu 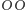 - to z pewnością zakończy się sukcesem Placka, natomiast przejście do
- to z pewnością zakończy się sukcesem Placka, natomiast przejście do 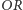 niekoniecznie skutkować będzie triumfem Jacka. Aby jednak przedstawić prawdopodobieństwa sukcesu graczy, musimy przeprowadzić nieco bardziej skomplikowane obliczenia niż poprzednio. Oznaczmy przez
niekoniecznie skutkować będzie triumfem Jacka. Aby jednak przedstawić prawdopodobieństwa sukcesu graczy, musimy przeprowadzić nieco bardziej skomplikowane obliczenia niż poprzednio. Oznaczmy przez 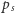 szansę na zwycięstwo Placka, gdy rozpoczynamy ze stanu
szansę na zwycięstwo Placka, gdy rozpoczynamy ze stanu 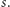 Wówczas oczywiście
Wówczas oczywiście 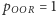 oraz
oraz 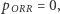 ponadto, korzystając z rysunku 2 oraz zdrowego rozsądku (przyjmującego w tym przypadku uczoną nazwę wzoru na prawdopodobieństwo całkowite), możemy przedstawić następujące zależności:
ponadto, korzystając z rysunku 2 oraz zdrowego rozsądku (przyjmującego w tym przypadku uczoną nazwę wzoru na prawdopodobieństwo całkowite), możemy przedstawić następujące zależności:
Z równania (1) dostajemy 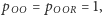 skąd oraz z układu równań (2) i (3) mamy
skąd oraz z układu równań (2) i (3) mamy 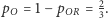 Z (4) wnioskujemy
Z (4) wnioskujemy 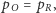 dlatego z równania (5) mamy
dlatego z równania (5) mamy 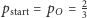 - jest to zatem szukane prawdopodobieństwo wygranej Placka na samym początku rozgrywki.
- jest to zatem szukane prawdopodobieństwo wygranej Placka na samym początku rozgrywki.
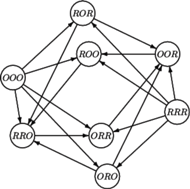
Rys. 3
Dążący do odzyskania przewagi nad swoim konkurentem Jacek może teraz przeprowadzić następujące rozumowanie: "skoro, obstawiając 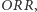 miałem przewagę nad celującym w
miałem przewagę nad celującym w 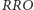 Plackiem, to jeśli teraz Placek wytypował
Plackiem, to jeśli teraz Placek wytypował 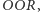 z symetrii sytuacji wystarczy mi zmienić swój wybór na
z symetrii sytuacji wystarczy mi zmienić swój wybór na 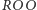 !". W odpowiedzi na takie posunięcie Placek może pomyśleć: "kiedy Jacek grał
!". W odpowiedzi na takie posunięcie Placek może pomyśleć: "kiedy Jacek grał 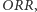 spuszczałem mu łomot, obstawiając
spuszczałem mu łomot, obstawiając 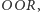 więc jeśli teraz wytypował
więc jeśli teraz wytypował 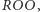 utrzymam moją przewagę, czekając na
utrzymam moją przewagę, czekając na 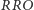 !". W tym miejscu artykułu Czytelnik, który nie zagubił się jeszcze w gąszczu e
!". W tym miejscu artykułu Czytelnik, który nie zagubił się jeszcze w gąszczu e 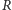 ów i
ów i 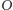 ów, zwrócił być może uwagę na pewien niepokojący efekt całego rozumowania. Uzasadniliśmy bowiem, że grający
ów, zwrócił być może uwagę na pewien niepokojący efekt całego rozumowania. Uzasadniliśmy bowiem, że grający 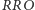 zapewne przegra z typującym
zapewne przegra z typującym 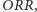 który powinien przegrać z obstawiającym
który powinien przegrać z obstawiającym 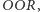 który prawdopodobnie ustąpi pola grającemu
który prawdopodobnie ustąpi pola grającemu 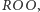 a ten ostatni zapewne poniesie klęskę, grając z... pierwszym, czyli
a ten ostatni zapewne poniesie klęskę, grając z... pierwszym, czyli 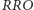 ! Oczywiście, sprzeczność jest jedynie pozorna, a podobnego typu paradoksów probabilistycznych nie brakuje - o jednym z nich (kościach Sichermana) można przeczytać w Delcie 1/2009. Czy możemy wskazać inne ciągi konfiguracji długości 3 o opisanej własności? Aby odpowiedzieć na to pytanie, użyjemy mało finezyjnego sposobu: dla każdych dwóch takich konfiguracji sprawdzimy bowiem, przy użyciu opisanej wcześniej metody, która z nich (o ile którakolwiek) miałaby większe szanse na wygraną w przypadku konfrontacji. Efekt takiej analizy przedstawiony jest na rysunku 3, na którym strzałka między dwiema konfiguracjami wskazuje na prawdopodobnego zwycięzcę, jej brak natomiast oznacza równe szanse w pojedynku. Zwróćmy uwagę, że konfiguracje
! Oczywiście, sprzeczność jest jedynie pozorna, a podobnego typu paradoksów probabilistycznych nie brakuje - o jednym z nich (kościach Sichermana) można przeczytać w Delcie 1/2009. Czy możemy wskazać inne ciągi konfiguracji długości 3 o opisanej własności? Aby odpowiedzieć na to pytanie, użyjemy mało finezyjnego sposobu: dla każdych dwóch takich konfiguracji sprawdzimy bowiem, przy użyciu opisanej wcześniej metody, która z nich (o ile którakolwiek) miałaby większe szanse na wygraną w przypadku konfrontacji. Efekt takiej analizy przedstawiony jest na rysunku 3, na którym strzałka między dwiema konfiguracjami wskazuje na prawdopodobnego zwycięzcę, jej brak natomiast oznacza równe szanse w pojedynku. Zwróćmy uwagę, że konfiguracje 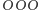 i
i 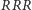 nie wygrywają z żadną inną, nie mogą być zatem częścią żadnego cyklu. Wynika stąd, że do cyklu nie mogą również należeć
nie wygrywają z żadną inną, nie mogą być zatem częścią żadnego cyklu. Wynika stąd, że do cyklu nie mogą również należeć 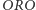 i
i 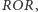 gdyż jedyne, z jakimi wygrywają, to wykluczone wcześniej
gdyż jedyne, z jakimi wygrywają, to wykluczone wcześniej 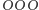 i
i 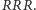 Z pozostałych konfiguracji można ułożyć wyłącznie cykl opisany wcześniej i dlatego jest on jedyny możliwy do uzyskania. Warto ponadto zauważyć, że z każdego wierzchołka prezentowanego grafu wychodzi strzałka - oznacza to, że dla każdej konfiguracji przeciwnika możemy znaleźć taką, która prawdopodobnie da nam zwycięstwo. Niestety, on może odpłacić się nam tym samym, i choć przez pewien czas moglibyśmy bawić się w złośliwe zmiany decyzji, patową sytuację zapewne najwygodniej będzie zakończyć przy użyciu starego i sprawdzonego pojedynczego rzutu monetą.
Z pozostałych konfiguracji można ułożyć wyłącznie cykl opisany wcześniej i dlatego jest on jedyny możliwy do uzyskania. Warto ponadto zauważyć, że z każdego wierzchołka prezentowanego grafu wychodzi strzałka - oznacza to, że dla każdej konfiguracji przeciwnika możemy znaleźć taką, która prawdopodobnie da nam zwycięstwo. Niestety, on może odpłacić się nam tym samym, i choć przez pewien czas moglibyśmy bawić się w złośliwe zmiany decyzji, patową sytuację zapewne najwygodniej będzie zakończyć przy użyciu starego i sprawdzonego pojedynczego rzutu monetą.