Niewymieniależność
Wyobraź sobie, Czytelniku, że na skutek wieloletnich ćwiczeń i poznania kilku szulerskich sztuczek udało Ci się zwiększyć swoje szanse na wygraną w grze blackjack do 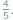 Kuszony wizją bajecznego bogactwa w końcu zdecydowałeś się odwiedzić kasyno, by tam spożytkować swoje niesamowite umiejętności. Z miną zawodowego pokerzysty przysiadłeś się do odpowiedniego stolika i zacząłeś grać...
Kuszony wizją bajecznego bogactwa w końcu zdecydowałeś się odwiedzić kasyno, by tam spożytkować swoje niesamowite umiejętności. Z miną zawodowego pokerzysty przysiadłeś się do odpowiedniego stolika i zacząłeś grać...
Oznaczmy przez 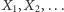 wyniki kolejnych gier, tzn.
wyniki kolejnych gier, tzn. 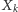 wynosi 1, jeśli w
wynosi 1, jeśli w 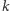 -tej grze odniosłeś sukces oraz 0 w przeciwnym przypadku. W naszych rozważaniach przyjmiemy, że zmienne
-tej grze odniosłeś sukces oraz 0 w przeciwnym przypadku. W naszych rozważaniach przyjmiemy, że zmienne 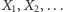 są niezależne, co w tym prostym przypadku oznacza dokładnie tyle, że dla dowolnego zero-jedynkowego ciągu
są niezależne, co w tym prostym przypadku oznacza dokładnie tyle, że dla dowolnego zero-jedynkowego ciągu 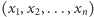 zachodzi
zachodzi
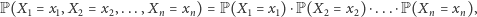
co, uwzględniwszy Twoje nadludzkie zdolności gry w blackjacka, pozwala nam stwierdzić, że
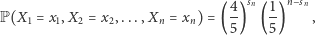
gdzie 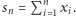 Zauważmy, że zgodnie z powyższą równością prawdopodobieństwo uzyskania dowolnego skończonego ciągu wyników w kolejnych grach nie zależy od kolejności, w jakiej te wyniki zostaną ustawione - innymi słowy, dla dowolnej permutacji
Zauważmy, że zgodnie z powyższą równością prawdopodobieństwo uzyskania dowolnego skończonego ciągu wyników w kolejnych grach nie zależy od kolejności, w jakiej te wyniki zostaną ustawione - innymi słowy, dla dowolnej permutacji 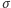 zbioru
zbioru 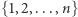 zachodzi
zachodzi

Własność tę nazywamy wymienialnością (ang. exchangeability) ciągu zmiennych 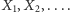 Ciąg wyników niezależnych powtórzeń dowolnego doświadczenia stanowi zatem ciąg wymienialny, jak się jednak zaraz okaże, nie jest to jedyna sytuacja, w jakiej możemy tę cechę zaobserwować.
Ciąg wyników niezależnych powtórzeń dowolnego doświadczenia stanowi zatem ciąg wymienialny, jak się jednak zaraz okaże, nie jest to jedyna sytuacja, w jakiej możemy tę cechę zaobserwować.

Załóżmy bowiem, że krupier - zaniepokojony Twoimi nadspodziewanie dobrymi rezultatami w blackjacku - zaproponował następujące urozmaicenie rozrywki. Tym razem masz rozpocząć grę od wyboru jednej z dwóch pozornie identycznych talii, przy czym jedna z nich jest zupełnie uczciwa, a druga - przeznaczona dla gości specjalnych - niezupełnie, co objawia się zmniejszeniem Twoich szans na wygraną do  Abstrahując od absurdalności opisanej sytuacji, przypuśćmy, że zdecydowałeś się przystać na ofertę krupiera. Zauważmy, że tym razem opisane w poprzednim akapicie zmienne
Abstrahując od absurdalności opisanej sytuacji, przypuśćmy, że zdecydowałeś się przystać na ofertę krupiera. Zauważmy, że tym razem opisane w poprzednim akapicie zmienne 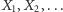 są zależne - intuicyjnie można się w tym miejscu powołać na fakt, że przegrana w pierwszej grze wpłynie na Twoją ocenę szans wygranej w drugiej grze (każe Ci bowiem przypuszczać, że wybrałeś nieuczciwą talię), a takie wnioskowanie nie może mieć miejsca przy zmiennych niezależnych. Mamy jednak w tej sytuacji do czynienia z warunkową niezależnością - jeśli bowiem mielibyśmy pracującego w kasynie przyjaciela, który zdradziłby nam, czy wybraliśmy uczciwą talię, to żadna informacja o dotychczasowym przebiegu naszych zmagań nie wpłynęłaby na ocenę szans na sukces w przyszłych rozgrywkach. Istotnie, jeśli przyjaciel opisał talię jako uczciwą, to nawet gdybyśmy doświadczyli 10 przegranych pod rząd, nasze szanse na powodzenie w 11 rozgrywce wciąż ocenialibyśmy na
są zależne - intuicyjnie można się w tym miejscu powołać na fakt, że przegrana w pierwszej grze wpłynie na Twoją ocenę szans wygranej w drugiej grze (każe Ci bowiem przypuszczać, że wybrałeś nieuczciwą talię), a takie wnioskowanie nie może mieć miejsca przy zmiennych niezależnych. Mamy jednak w tej sytuacji do czynienia z warunkową niezależnością - jeśli bowiem mielibyśmy pracującego w kasynie przyjaciela, który zdradziłby nam, czy wybraliśmy uczciwą talię, to żadna informacja o dotychczasowym przebiegu naszych zmagań nie wpłynęłaby na ocenę szans na sukces w przyszłych rozgrywkach. Istotnie, jeśli przyjaciel opisał talię jako uczciwą, to nawet gdybyśmy doświadczyli 10 przegranych pod rząd, nasze szanse na powodzenie w 11 rozgrywce wciąż ocenialibyśmy na 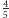 (o ile jeszcze nie zaczęliśmy się zastanawiać, czy aby na pewno nasz przyjaciel jest naszym przyjacielem). Jeśli więc przez
(o ile jeszcze nie zaczęliśmy się zastanawiać, czy aby na pewno nasz przyjaciel jest naszym przyjacielem). Jeśli więc przez 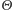 oznaczymy naszą szansę na sukces przy grze wybranymi kartami (
oznaczymy naszą szansę na sukces przy grze wybranymi kartami ( 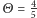 dla uczciwej talii, w przeciwnym przypadku
dla uczciwej talii, w przeciwnym przypadku 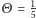 ), to dla dowolnej liczby naturalnej
), to dla dowolnej liczby naturalnej  oraz permutacji
oraz permutacji 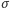 zbioru
zbioru 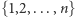 możemy zapisać
możemy zapisać
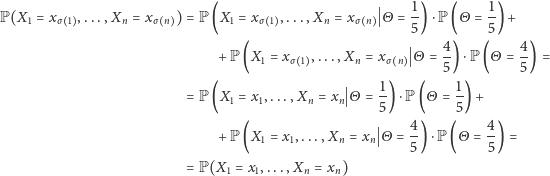
Oznacza to, że podobnie jak w poprzednim przypadku kolejne wyniki tworzą ciąg wymienialny. Analogiczne rozumowanie moglibyśmy przeprowadzić, gdyby zmienna, pod warunkiem której kolejne gry są niezależne z tym samym prawdopodobieństwem sukcesu, była dużo bardziej skomplikowana (na przykład gdybyśmy na początku w jednostajny sposób losowy wybierali z odcinka ![|[0,1]](/math/temat/matematyka/rachunek_prawdopodobienstwa/2015/08/26/Niewymienialeznosc/11x-9a78746528227503495503a32cffe4a6bda23331-im-33,33,33-FF,FF,FF.gif) prawdopodobieństwo wygranej w kolejnych grach). Rozważania te prowadzą do naturalnego pytania: czy możemy skonstruować nieskończony ciąg doświadczeń losowych o wymienialnych rezultatach (w sensie sukcesu lub porażki) w inny sposób niż poprzez niezależne kopie tego samego eksperymentu z losowo wybranym na początku prawdopodobieństwem sukcesu?
prawdopodobieństwo wygranej w kolejnych grach). Rozważania te prowadzą do naturalnego pytania: czy możemy skonstruować nieskończony ciąg doświadczeń losowych o wymienialnych rezultatach (w sensie sukcesu lub porażki) w inny sposób niż poprzez niezależne kopie tego samego eksperymentu z losowo wybranym na początku prawdopodobieństwem sukcesu?
Zanim odpowiemy na to pytanie, zastanówmy się, w jaki sposób możemy w trakcie rozgrywki z krupierem przekonać się, którą z talii wybraliśmy - innymi słowy, jaką wartość zmiennej 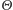 wylosowaliśmy. Odpowiedź jest mocno intuicyjna - spodziewamy się, że wraz ze wzrostem liczby gier coraz lepszym przybliżeniem prawdopodobieństwa wygranej będzie udział naszych zwycięstw we wszystkich dotychczasowych grach. Przekładając tę intuicję na wprowadzone oznaczenia, możemy zapisać
wylosowaliśmy. Odpowiedź jest mocno intuicyjna - spodziewamy się, że wraz ze wzrostem liczby gier coraz lepszym przybliżeniem prawdopodobieństwa wygranej będzie udział naszych zwycięstw we wszystkich dotychczasowych grach. Przekładając tę intuicję na wprowadzone oznaczenia, możemy zapisać
 |
(1) |
Powyższa zależność okaże się wskazówką do udowodnienia następującego twierdzenia
Twierdzenie (de Finettiego). Jeśli nieskończony ciąg doświadczeń 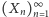 jest wymienialny, to istnieje zmienna - wyżej określona
jest wymienialny, to istnieje zmienna - wyżej określona 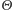 - pod warunkiem której zmienne
- pod warunkiem której zmienne 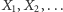 są niezależne i mają ten sam rozkład.
są niezależne i mają ten sam rozkład.

Wyobraź sobie teraz, Czytelniku, że krupier zaproponował Ci nową grę i z jego wieloletniego doświadczenia wynika, że rezultaty kolejnych rozgrywek tworzą ciąg wymienialny. Przypuśćmy, że chwilę po rozpoczęciu zabawy przysiada się do Ciebie wysoki, elegancko ubrany dżentelmen o prawym oku czarnym, a lewym zielonym. Nachyla się do Twojego ucha i szepcze z cudzoziemskim akcentem "Annuszka kupiła już olej słonecznikowy, a po setnej grze będziesz miał dwadzieścia wygranych", po czym ulatnia się tak nagle, jak się pojawił. Coś w jego wyglądzie każe Ci zawierzyć usłyszanej przepowiedni, dlatego czym prędzej sięgasz po coś do pisania i obliczasz, w jaki sposób uzyskana informacja wpływa na Twoją ocenę opłacalności gry w kolejnych rundach. Przyjmując oznaczenie 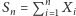 na liczbę sukcesów po
na liczbę sukcesów po  -tej rozgrywce oraz dając wiarę zapewnieniom krupiera o wymienialności ciągu wyników, stwierdzamy, że
-tej rozgrywce oraz dając wiarę zapewnieniom krupiera o wymienialności ciągu wyników, stwierdzamy, że
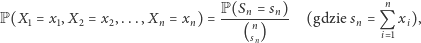 |
(2) |
gdyż każdy z 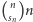 -wyrazowych ciągów wyników z
-wyrazowych ciągów wyników z  sukcesami jest równie prawdopodobny. Spróbujmy teraz obliczyć prawdopodobieństwo uzyskania
sukcesami jest równie prawdopodobny. Spróbujmy teraz obliczyć prawdopodobieństwo uzyskania 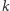 sukcesów w
sukcesów w  -tej rundzie, gdzie
-tej rundzie, gdzie 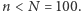 Pamiętajmy, że po
Pamiętajmy, że po 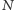 -tej rundzie mamy mieć na koncie
-tej rundzie mamy mieć na koncie 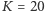 zwycięstw. Każda z permutacji tych
zwycięstw. Każda z permutacji tych 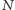 przyszłych wyników jest równie prawdopodobna, zastanówmy się zatem, jak wiele z nich oznacza
przyszłych wyników jest równie prawdopodobna, zastanówmy się zatem, jak wiele z nich oznacza 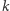 sukcesów po
sukcesów po 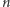 rundach. Najpierw musimy wybrać
rundach. Najpierw musimy wybrać 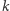 zwycięskich rund spośród pierwszych
zwycięskich rund spośród pierwszych  na
na  sposobów, następnie
sposobów, następnie 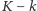 pozostałych sukcesów spomiędzy
pozostałych sukcesów spomiędzy 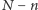 końcowych rozgrywek na
końcowych rozgrywek na 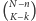 sposobów. Ponadto zwycięskie rundy możemy pomieszać na
sposobów. Ponadto zwycięskie rundy możemy pomieszać na 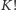 sposobów, a przegrane na
sposobów, a przegrane na 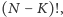 co przy
co przy 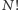 wszystkich możliwych permutacji daje nam równość
wszystkich możliwych permutacji daje nam równość

gdzie 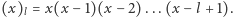 Niestety, w kasynie nie powinniśmy liczyć na pomoc sił nadprzyrodzonych, jednak uzyskana wyżej równość i tak może być użyteczna dla naszych celów. Zauważmy bowiem, że nawet jeśli nie znamy wartości
Niestety, w kasynie nie powinniśmy liczyć na pomoc sił nadprzyrodzonych, jednak uzyskana wyżej równość i tak może być użyteczna dla naszych celów. Zauważmy bowiem, że nawet jeśli nie znamy wartości 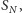 to - korzystając ze wzoru na prawdopodobieństwo całkowite - możemy uzyskać
to - korzystając ze wzoru na prawdopodobieństwo całkowite - możemy uzyskać
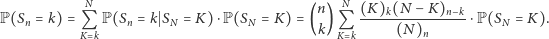
Przyjmijmy teraz oznaczenie 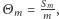 co pozwoli powyższą zależność przepisać w postaci
co pozwoli powyższą zależność przepisać w postaci
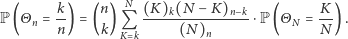
Jest ona prawdziwa dla dowolnych liczb naturalnych 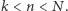 Ustalmy teraz
Ustalmy teraz  i zwiększajmy
i zwiększajmy 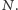 Niestety, nie możemy jeszcze stwierdzić, że zmienne
Niestety, nie możemy jeszcze stwierdzić, że zmienne  zbiegają w jakimś sensie do jednej zmiennej. Wszystkie jednak są zmiennymi na
zbiegają w jakimś sensie do jednej zmiennej. Wszystkie jednak są zmiennymi na ![[0, | 1]](/math/temat/matematyka/rachunek_prawdopodobienstwa/2015/08/26/Niewymienialeznosc/33x-1f9793a301520ef5f07d9d0b8be11b45066f47fa-im-33,33,33-FF,FF,FF.gif) - okazuje się, że w tej sytuacji jest im na tyle ciasno, że jesteśmy w stanie wybrać z nich podciąg
- okazuje się, że w tej sytuacji jest im na tyle ciasno, że jesteśmy w stanie wybrać z nich podciąg 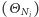 zbieżny (w pewnym sensownym sensie) do konkretnej zmiennej losowej
zbieżny (w pewnym sensownym sensie) do konkretnej zmiennej losowej 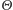 na
na ![[0,1].](/math/temat/matematyka/rachunek_prawdopodobienstwa/2015/08/26/Niewymienialeznosc/36x-1f9793a301520ef5f07d9d0b8be11b45066f47fa-im-33,33,33-FF,FF,FF.gif) Wyobraźmy sobie teraz, że wspomniany wcześniej tajemniczy cudzoziemiec zdradził nam, że gdybyśmy grali w nieskończoność, zmienna
Wyobraźmy sobie teraz, że wspomniany wcześniej tajemniczy cudzoziemiec zdradził nam, że gdybyśmy grali w nieskończoność, zmienna 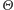 osiągnęłaby wartość
osiągnęłaby wartość 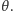 Przeprowadzając poprzednie rozumowanie, moglibyśmy wówczas dojść do równości
Przeprowadzając poprzednie rozumowanie, moglibyśmy wówczas dojść do równości
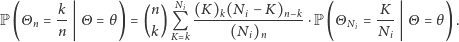 |
(3) |
dla dowolnej liczby naturalnej 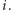 Okazuje się teraz, iż wraz ze wzrostem
Okazuje się teraz, iż wraz ze wzrostem 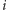
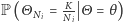 "koncentruje się" wokół
"koncentruje się" wokół 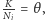 tzn. jeśli wybierzemy dowolnie małe otoczenie
tzn. jeśli wybierzemy dowolnie małe otoczenie 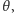 to suma wspomnianych prawdopodobieństw dla
to suma wspomnianych prawdopodobieństw dla  spoza tego otoczenia będzie zbiegała do 0,
spoza tego otoczenia będzie zbiegała do 0,- różnica między
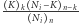 a
a 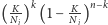 zbiega do 0. By się o tym przekonać, wystarczy sprawdzić, że oba ciągi są ograniczone, a ich iloraz zbiega do 1.
zbiega do 0. By się o tym przekonać, wystarczy sprawdzić, że oba ciągi są ograniczone, a ich iloraz zbiega do 1.
Powyższe uwagi miały za zadanie skłonić Czytelnika, by uwierzył, że dysponując odpowiednim zapasem cierpliwości i zręcznością w posługiwaniu się epsilonami i deltami, można wykazać, że prawa strona równania (3) zbiega do 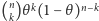 przy
przy 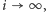 co oczywiście pociąga za sobą
co oczywiście pociąga za sobą 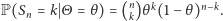 Korzystając z "warunkowego" odpowiednika równości (2), dostajemy zatem
Korzystając z "warunkowego" odpowiednika równości (2), dostajemy zatem
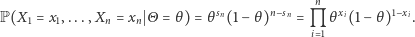
Oznacza to dokładnie tyle, że przy ustalonej wartości zmiennej 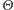 wymienialne zmienne
wymienialne zmienne 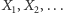 są niezależne oraz wszystkie mają ten sam rozkład o prawdopodobieństwie sukcesu wskazywanym przez
są niezależne oraz wszystkie mają ten sam rozkład o prawdopodobieństwie sukcesu wskazywanym przez 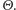 Innymi słowy, pracujący w kasynie analityk nie byłby w stanie, bazując wyłącznie na wynikach, odróżnić naszej gry od takiej, która polegałaby na niezależnych powtórzeniach tej samej rozgrywki z prawdopodobieństwem sukcesu określonym a priori przy użyciu zmiennej
Innymi słowy, pracujący w kasynie analityk nie byłby w stanie, bazując wyłącznie na wynikach, odróżnić naszej gry od takiej, która polegałaby na niezależnych powtórzeniach tej samej rozgrywki z prawdopodobieństwem sukcesu określonym a priori przy użyciu zmiennej 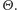 A skoro tak, to na mocy równości (1) zmienna ta - określona wcześniej jako granica podciągu
A skoro tak, to na mocy równości (1) zmienna ta - określona wcześniej jako granica podciągu  - jest również granicą całego ciągu
- jest również granicą całego ciągu  której istnienia nie mogliśmy wcześniej założyć.
której istnienia nie mogliśmy wcześniej założyć.
Czy jednak krupier byłby w stanie zaproponować nam grę, w której istnienie wspomnianej granicy byłoby nieoczywiste? Okazuje się, że tak, i przykład nie jest specjalnie skomplikowany. Wyobraźmy sobie, że postawiono przed nami urnę, w której znajdują się dwie kule - jedna biała, druga czarna. W każdej rundzie wyciągamy z urny jedną kulę, a następnie wkładamy ją z powrotem wraz z jeszcze jedną kulą tego samego koloru. Rundę uznajemy za wygraną, jeśli wyciągnęliśmy w niej kulę białą. Oczywiście, kolejne rozgrywki nie są powtarzaniem tego samego doświadczenia - każde wyciągnięcie białej kuli zwiększa prawdopodobieństwo sukcesu w kolejnej rundzie. Łatwo można jednak wykazać, że otrzymywane wyniki tworzą ciąg zmiennych wymienialnych. Aby się o tym przekonać, wystarczy w tym przypadku stwierdzić, że zamiana ostatnich dwóch wyników w dowolnym ciągu początkowych rezultatów nie zmieni nam prawdopodobieństwa jego uzyskania pod warunkiem wcześniejszych wyników. Niech zatem 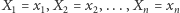 będzie ciągiem
będzie ciągiem  pierwszych wyników. Jeśli
pierwszych wyników. Jeśli 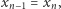 postulowana równość jest oczywista. Bez straty ogólności przyjmijmy zatem
postulowana równość jest oczywista. Bez straty ogólności przyjmijmy zatem 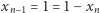 i wówczas otrzymamy
i wówczas otrzymamy
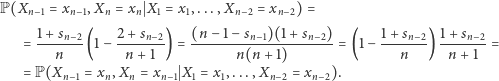
Zgodnie z naszymi wcześniejszymi obserwacjami oznacza to ich niezależność i ten sam rozkład pod warunkiem znajomości (istniejącej) granicy 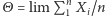 - gdyby tajemniczy cudzoziemiec zdradził nam jej wartość
- gdyby tajemniczy cudzoziemiec zdradził nam jej wartość 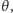 to szansę na sukces w każdej kolejnej rundzie ocenialibyśmy właśnie na
to szansę na sukces w każdej kolejnej rundzie ocenialibyśmy właśnie na  Wydaje się to dosyć zaskakujące, zwłaszcza jeśli przeprowadzimy podobne rozumowanie przy założeniu, że początkowo w urnie znajdowały się jedna kula biała i 100 czarnych oraz dostaliśmy informację
Wydaje się to dosyć zaskakujące, zwłaszcza jeśli przeprowadzimy podobne rozumowanie przy założeniu, że początkowo w urnie znajdowały się jedna kula biała i 100 czarnych oraz dostaliśmy informację 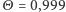 - choć serce drżałoby z trwogi, zimna kalkulacja nakazywałaby już w pierwszej rundzie stawiać na szali zwycięstwa wszystkie nasze oszczędności, dom, psa i ubranie, gdyż szansa na sukces i tak wynosiłaby
- choć serce drżałoby z trwogi, zimna kalkulacja nakazywałaby już w pierwszej rundzie stawiać na szali zwycięstwa wszystkie nasze oszczędności, dom, psa i ubranie, gdyż szansa na sukces i tak wynosiłaby 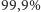 ! Cały sekret tkwi w fakcie, że pozornie duże prawdopodobieństwo porażki w pierwszym losowaniu jest "pożerane" przez informację o tak dużej (lecz również tak mało prawdopodobnej) wartości
! Cały sekret tkwi w fakcie, że pozornie duże prawdopodobieństwo porażki w pierwszym losowaniu jest "pożerane" przez informację o tak dużej (lecz również tak mało prawdopodobnej) wartości 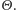 Przy naszych założeniach prawdopodobieństwo zdarzenia, że
Przy naszych założeniach prawdopodobieństwo zdarzenia, że 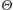 jest nie mniejsze od
jest nie mniejsze od  jest rzędu
jest rzędu 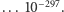 Nie trzeba wielkiej przenikliwości umysłu, by stwierdzić, że w tej sytuacji nasz cudzoziemiec z pewnością nie jest żadnym Bułhakowowskim Wolandem, a jedynie zwykłym hochsztaplerem. No, może nie z pewnością, a prawdopodobnie, więc może na wszelki wypadek uważajmy na plamy rozlanego oleju...
Nie trzeba wielkiej przenikliwości umysłu, by stwierdzić, że w tej sytuacji nasz cudzoziemiec z pewnością nie jest żadnym Bułhakowowskim Wolandem, a jedynie zwykłym hochsztaplerem. No, może nie z pewnością, a prawdopodobnie, więc może na wszelki wypadek uważajmy na plamy rozlanego oleju...
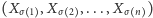 od wyboru permutacji
od wyboru permutacji 


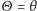 zmienne
zmienne  zbiegają według rozkładu do stałej, a zatem zbieżność ta jest również według prawdopodobieństwa, co tłumaczy pierwszą kropkę.
zbiegają według rozkładu do stałej, a zatem zbieżność ta jest również według prawdopodobieństwa, co tłumaczy pierwszą kropkę.